№12. Определить приближенное значение коэффициента трения песка о стекло. Оборудование: песочные часы, линейка.

Решение.   Чтобы песочные часы оправдывали свое назначение, песок в них должен течь равномерно. Из рисунка видно, что песчинки будут двигаться равномерно, если сумма сил, действующих на них, будет равна нулю.  Тело, находящееся на наклонной плоскости, будет двигаться равномерно при условии, что tgα = μ, где μ − коэффициент трения.

 Таким образом, наша задача сводится к определению tgα. Нетрудно видеть (рис.), что tgα = |OO₁|/|AO₁|; |AO₁| = (1/2)|AB|, |OO₁| = (1/2)√{4|AO|² − |AB|²}, тогда tgα = √{4|AO|² − |AB|²}/|AB|. Теперь осталось измерить величину |AO| и |AB|, что легко сделать с помощью линейки.

№13. Определить коэффициент трения бруска о горизонтальный стол, если длина и ширина бруска меньше его высоты.

 Оборудование: брусок, нить, линейка.

 Решение.  Для того чтобы брусок сдвинуть с места, необходимо у его основания ABCD (места приложения сил трения) подействовать силой F. Запишем условие равномерного движения бруска по поверхности стола:

F = F_mp. (1) Если силу F переносить параллельно вверх от основания АВСD (рис.),

то равномерное и прямолинейное движение бруска будет продолжаться, а брусок не будет поворачиваться относительно ребра основания DC до тех пор, пока вращающий момент силы не превысит момент силы тяжести mg относительно DC. Тогда из условия Fh = mga/2 (2) находим, что

F = mga/(2h), (3) где h − плечо силы F, при котором брусок начинает переворачиваться. Коэффициент трения μ = F_mp/(mg). Из уравнений (1) и (3) находим, что μ = a/(2h).

№14. Исследовать зависимость кпд наклонной плоскости от угла ее наклона к горизонту. Оборудование: трибометр, брусок, линейка ученическая, секундомер.

 Решение.

Как известно, КПД наклонной плоскости (рис.)

η = (A_n/A_c)•100 %,

где А_n = F_тяг/l − полезная работа, т. е. работа по равномерному подъему тела без трения (l − длина наклонной плоскости), а А_с = F_тягl − работа при наличии трения (совершенная работа). Запишем второй закон Ньютона для равномерного движения F_тяг + F_mp + N + mg = 0 (в векторном виде). В проекции на оси координат после несложных преобразований получим:

F_тяг = mg(sinα + μcosα). Если трение отсутствует, то μ = 0 и тогда F_тяг^/ = mgsinα.Таким образом, η = sinα/(sinα + μcosα), или η = 1/(1 + μctgα).

Отсюда следует, что для того, чтобы найти η как функцию угла α, надо знать коэффициент трения μ. Для определения μ подберем угол наклона α₀ трибометра (наклонной плоскости) таким образом, чтобы брусок двигался вниз с небольшим (подумайте почему) ускорением. Тогда

l = at²/2. (1) Длину наклонной плоскости l измеряем линейкой. Время движения определим по секундомеру. Из выражения (1) имеем: а = 2l/t². (2) Из второго закона Ньютона имеем: ma = mgsinα₀ − μmgcosα₀. (3) Совместное решение уравнений (2) и (3) дает: μ = (gsinα_o − 2l/t²)/(gcosα_o). (4) Преобразовав выражение (4), имеем: μ = tgα_o − 2l/(gt²cosα_o).  Измерив КПД наклонной плоскости при различных углах наклона, следует отметить полученные значения КПД на графике η = f(α).

№15. На каком максимальном расстоянии от центра диска электропроигрывателя может удержаться монета при вращении с заданной угловой скоростью?

Оборудование: проигрыватель, медная монета.

 Решение.  Так как монета вращается, то на нее действует центростремительная сила

F_ц = ma_ц = 4π²Rmv², (1) где m − масса монеты, R − расстояние от центра диска до центра монеты, ν − частота вращения диска. В данном случае центростремительной силой будет являться сила трения F_mp = μmg, (2) где g − ускорение свободного падения, μ − коэффициент трения. Приравняем выражения (1) и (2): μmg = 4π²Rmv², откуда:

R = μg/(4π²ν²). Коэффициент трения ν = tgα_o находим из предварительных опытов по определению предельного угла α_o наклона диска, при котором монета начинает скользить по диску. В этом случае, как известно,

μ = tgα_o. Окончательно получаем, что монета может удержаться на расстоянии R = gtgα_o/(4π²ν²).

Вычислительные задачи по механике

№1 Из пру­жин­но­го пи­сто­ле­та вы­стре­ли­ли вер­ти­каль­но вниз в ми­шень, на­хо­дя­щу­ю­ся на рас­сто­я­нии 2 м от него. Со­вер­шив ра­бо­ту 0,12 Дж, пуля застря­ла в ми­ше­ни. Ка­ко­ва масса пули, если пру­жи­на была сжата перед выстре­лом на 2 см, а ее жест­кость 100 Н/м?

№2 Найти силу трения, действующую на груз массой m (см. рис), ускорение движения грузов и силу натяжения нити, если h=60 см, L=1м, m=0,5 кг, µ=0,25. Решить задачу при следующих значениях массы груза M:

а) 0,1 кг; б) 0,25 кг; в) 0,3 кг; г) 0,35 кг; д) 0,5 кг.

№3. Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рисунок). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α=30˚, коэффициент трения µ=0,3). Чему равно максимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?

№4. Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рисунок). В точке В наклонная плоскость без излома переходи в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит =4м/с, то в точке В шайба отрывается от опоры. Длина наклонной плоскости AB=L=1м, угол α=30˚. Коэффициент трения между наклонной плоскостью и шайбой µ=0,2. Найдите внешний радиус трубы R.

№5. С какой скоростью внутри сферы радиусом R=10 cм должен вращаться небольшой шарик, чтобы он все время находился на высоте h=5 cм относительно нижней точки сферы? (см. рис)

№6. Определите отношение масс грузов, находящихся на двух поверхностях клина в равновесии (см. рис). Углы у основания клина α и β. Коэффициент трения µ.

Ре­ше­ние.

Со­глас­но за­ко­ну со­хра­не­ния ме­ха­ни­че­ской энер­гии, имеем два ра­вен­ства:

     (1),

     (2),

где и  — ско­ро­сти ле­тя­щей пули со­от­вет­ствен­но на вы­со­те и не­по­сред­ствен­но перед ми­ше­нью. Вся энер­гия под­ле­тев­шей к ми­ше­ни пули по­тра­че­на на ме­ха­ни­че­скую ра­бо­ту, так что      (3).

№7. Кусок пла­сти­ли­на стал­ки­ва­ет­ся со сколь­зя­щим нав­стре­чу по го­ри­зон­таль­ной по­верх­но­сти стола брус­ком и при­ли­па­ет к нему. Ско­ро­сти пла­сти­ли­на и брус­ка перед уда­ром на­прав­ле­ны про­ти­во­по­лож­но и равны и . Масса брус­ка в 4 раза боль­ше массы пла­сти­ли­на. Ко­эф­фи­ци­ент тре­ния сколь­же­ния между брус­ком и сто­лом . На какое рас­сто­я­ние пе­ре­ме­стят­ся слип­ши­е­ся бру­сок с пла­сти­ли­ном к мо­мен­ту, когда их ско­рость умень­шит­ся на 30%?

№8. На по­след­нем ав­то­са­ло­не в Дет­рой­те фирма «Мер­се­дес» пред­ста­ви­ла новый род­стер с дви­га­те­лем объёмом 4,7 литра, спо­соб­ный раз­го­нять­ся от 0 до 100 км/ч за 4,8 се­кун­ды. Счи­тая, что про­цесс раз­го­на про­ис­хо­дит по го­ри­зон­та­ли и яв­ля­ет­ся рав­но­уско­рен­ным, опре­де­ли­те, под каким углом к го­ри­зон­ту на­прав­ле­на сила, дей­ству­ю­щая на во­ди­те­ля со сто­ро­ны си­де­нья во время та­ко­го раз­го­на.

№9. Из двух ров­ных досок сде­лан желоб, пред­став­ля­ю­щий собой двугран­ный угол с рас­тво­ром . Желоб за­креп­лен так, что его ребро гори­зон­таль­но, а доски сим­мет­рич­ны от­но­си­тель­но вер­ти­ка­ли. В же­ло­бе на бо­ко­вой по­верх­но­сти лежит ци­линдр мас­сой m=2кг. Ко­эф­фи­ци­ент тре­ния между дос­ка­ми и ци­лин­дром равен . К торцу ци­лин­дра при­ло­же­на гори­зон­таль­но на­прав­лен­ная сила F=3Н. Най­ди­те мо­дуль уско­ре­ния цилиндра.

№10. При­бор на­блю­де­ния об­на­ру­жил ле­тя­щий сна­ряд и за­фик­си­ро­вал его горизонтальную ко­ор­ди­на­ту x и вы­со­ту над Землёй (см. ри­су­нок). Через 3 с сна­ряд упал на Землю и взо­рвал­ся на рас­сто­я­нии = 1700 м от места его об­на­ру­же­ния. Чему рав­ня­лось время полёта сна­ря­да от пушки до места взры­ва, если счи­тать, что со­про­тив­ле­ние воз­ду­ха пре­не­бре­жи­мо мало? Пушка и место взры­ва на­хо­дят­ся на одной го­ри­зон­та­ли.

№11. Сна­ряд мас­сой 4 кг, ле­тя­щий со ско­ро­стью 400 м/с, раз­ры­ва­ет­ся на две рав­ные части, одна из ко­то­рых летит в на­прав­ле­нии дви­же­ния сна­ря­да, а дру­гая — в про­ти­во­по­лож­ную сто­ро­ну. В мо­мент раз­ры­ва сум­мар­ная ки­не­ти­че­ская энер­гия оскол­ков уве­ли­чи­лась на ве­ли­чи­ну . Ско­рость оскол­ка, ле­тя­ще­го по на­прав­ле­нию дви­же­ния сна­ря­да, равна 900 м/с. Най­ди­те .

№12. При вы­пол­не­нии трюка «Ле­та­ю­щий ве­ло­си­пе­дист» гон­щик движет­ся по трам­пли­ну под дей­стви­ем силы тя­же­сти, на­чи­ная дви­же­ние из со­сто­я­ния покоя с вы­со­ты Н (см. ри­су­нок). На краю трам­пли­на ско­рость гонщи­ка на­прав­ле­на под углом к го­ри­зон­ту. Про­ле­тев по воз­ду­ху, гон­щик при­зем­ля­ет­ся на го­ри­зон­таль­ный стол, на­хо­дя­щий­ся на той же вы­соте, что и край трам­пли­на. Ка­ко­ва вы­со­та по­ле­та h на этом трам­пли­не? Сопро­тив­ле­ни­ем воз­ду­ха и тре­ни­ем пре­не­бречь.

№13. На глад­кой го­ри­зон­таль­ной по­верх­но­сти стола по­ко­ит­ся горка с двумя вер­ши­на­ми, вы­со­ты ко­то­рых h и 4h (см. ри­су­нок). На пра­вой вер­ши­не горки на­хо­дит­ся шайба. Масса горки в 8 раз боль­ше массы шайбы. От не­зна­чи­тель­но­го толч­ка шайба и горка при­хо­дят в дви­же­ние, причём шайба дви­жет­ся влево, не от­ры­ва­ясь от глад­кой по­верх­но­сти горки, а по­сту­па­тель­но движу­ща­я­ся горка не от­ры­ва­ет­ся от стола. Най­ди­те ско­рость шайбы на левой вер­ши­не горки.

№14. Два ма­лень­ких тела бро­са­ют вер­ти­каль­но вверх из одной точки через про­ме­жу­ток вре­ме­ни Δt = 3 c со ско­ро­стя­ми V₁ = 20 м/с и V₂ = 10 м/с. На какой вы­со­те H тела столк­нут­ся? Со­про­тив­ле­ни­ем воз­ду­ха можно пре­не­бречь.

№15. На гра­ни­це раз­де­ла двух не­сме­ши­ва­ю­щих­ся жид­ко­стей, име­ю­щих плот­но­сти ρ₁ = 900 кг/м3 и ρ₂ = 3ρ₁, пла­ва­ет шарик (см. ри­су­нок). Ка­ко­ва долж­на быть плот­ность ша­ри­ка ρ, чтобы выше гра­ни­цы раз­де­ла жид­ко­стей была одна треть его объёма?

Графические задачи.

№1 Мячик бросают с земли вертикально вверх с начальной скоростью v_о. Постройте график зависимости скорости мячика от времени, считая удары о землю абсолютно упругими. Сопротивлением воздуха пренебречь.

Решение.

Мячик движется равноускоренно в поле силы тяжести. В начальный момент проекция скорости на вертикальную ось равна v_o. Через время v_o/g скорость обращается в ноль, а еще через такое же время ее проекция равна −v_o. В моменты удара о землю скорость мгновенно меняет направление на противоположное. Поэтому искомый график состоит из отрезков прямых.

№2 Пассажир, опоздавший к поезду, заметил, что предпоследний вагон прошел мимо него за t₁ = 10 c, а последний — за t₂ = 8 с. Считая движение поезда равноускоренным, определите время опоздания.

Решение:

Графическое решение данной задачи основано на том, что площадь под графиком скорости численно равна пройденному пути за время t₁ и t₂ — это равные длины вагонов, поэтому:

№3. В комнате высотой H к потолку одним концом прикреплена легкая пружина жесткостью k, имеющая в недеформированном состоянии длину l_о (l_о < H). На полу под пружиной размещают брусок высотой x с площадью основания S, изготовленный из материала плотностью ρ. Построить график зависимости давления бруска на пол от высоты бруска.

Если x < H − l_o, то пружина не касается бруска. В этом случае давление определяется формулой:

p = ρgx.

Если x > H − l_o, пружина будет сжиматься и давить на брусок. Величина сжатия:

lo + x − H,

действующая сила по закону Гука:

F = k(lo + x − H).

№4. К бруску массой 10 кг, находящемуся на горизонтальной поверхности, приложена сила. Учитывая, что коэффициент трения равен 0,7, определите:

• cилу трения для случая, если F = 50 Н и направлена горизонтально.

• cилу трения для случая, если F = 80 Н и направлена горизонтально.

• построить график зависимости ускорения бруска от горизонтально приложенной силы.

• с какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать брусок?  

Решение:

№6. Имеются две трубы, подсоединенных к смесителю. На каждой из труб имеется кран, которым можно регулировать поток воды по трубе, изменяя его от нуля до максимального значения J_o = 1 л/с. В трубах течет вода с температурами t₁ = 10° C и t₂ = 50° C. Постройте график зависимости максимального потока воды, вытекающей из смесителя, от температуры этой воды. Тепловыми потерями пренебречь.

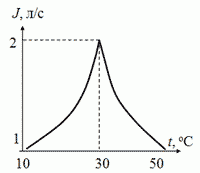
Предложения по оценке итогового графика. На графике должна быть видна следующая информация:

1. график состоит из двух частей, возрастающей и убывающей;

2. график построен в диапазоне температур t₁ < t < t₂;

3. на графике указаны координаты трех угловых точек, а именно:

   • t = 10°C, J = 1 л/с,

   • t = 30°C, J = 2 л/с,

   • t = 50°C, J = 1 л/с.

Поздним вечером молодой человек ростом h идет по краю горизонтального прямого тротуара с постоянной скоростью v. На расстоянии l от края тротуара стоит фонарный столб. Горящий фонарь закреплен на высоте H от поверхности земли. Постройте график зависимости скорости движения тени головы человека от координаты x.  

Решение:

№ 7. На рисунке представлен график зависимости скорости v автомобиля от времени t. Найдите путь, пройденный автомобилем за 5 с.

№8. Тело движется по оси Ох. На графике показана зависимость проекции скорости тела на ось Ох от времени. Каков путь, пройденный телом к моменту времени t = 4c?

№9. На рисунке приведен график зависимости проекции ускорения некоторого тела от времени. Считая проекцию начальной скорости равной 10 м/с, напишите уравнение зависимости Vₓ (t) и постройте ее график.

№10. По графику скорости, построить график перемещения.

Решение.

Чтобы построить график, необходимо определить вид зависимости S_x (t). Из графика видим, что  V_x = const → движение равномерное прямолинейное → S_x (t) = V_x· t. Из графика V_x = 5 м/с → S_x (t) = 5t. Линейная зависимость, график – прямая линия под углом к осям. Для построения достаточно двух точек. Точки выбираем произвольно. Строим график.

№11. В первом опыте груз совершает гармонические колебания по закону x(t) = 3cos(5πt), где координата измеряется в см. Во втором опыте период колебаний увеличивают в 2 раза, оставив амплитуду неизменной. Какой из приведенных ниже графиков правильно отображает зависимость координаты груза от времени во втором опыте?

№12. На рисунке представлен график зависимости скорости υ автомобиля от времени

t. Найдите путь, пройденный автомобилем за 5 с.

№13. Тело движется вдоль оси Ох, причем проекция скорости x меняется с течением времени по закону, приведенному на графике. Какой путь прошло тело за время от 4 до 16 с?

№14. Тело движется вдоль оси OX. На рисунке приведен графикзависимости проекции скорости этого тела vx от времени t. Какой путьпрошло тело за промежуток времени от t1= 2 с до t2= 5 с?

№15. По заданному графику перемещения построить график скорости.

Решение.

Зависимость перемещения от времени линейная. Следовательно, движение равномерное прямолинейное, то есть скорость постоянна → графиком является прямая линия параллельная оси времени. По графику S_x (t) определяем скорость и строим график.