
- •Принцип роботи
- •6.1. Конструкція та принцип роботи транзисторів
- •6.2. Схеми увімкнення транзисторів
- •6.3. Статичні характеристики транзисторів
- •6.4. Еквівалентні схеми транзисторів
- •6.5. Робочий режим транзисторів
- •6.6. Живлення кола бази транзистора
- •6.7. Температурна стабілізація робочої точки транзистора
- •6.8. Порядок розрахунку підсилювального каскаду на біполярному транзисторі в схемі з фіксованою напругою бази та термостабілізацією робочої точки з допомогою нзз за постійним струмом
- •6.9. Частотні властивості транзисторів
- •6.10. Імпульсні властивості транзисторів
- •6.11. Основні параметри граничних режимів роботи транзистора та вплив температури на параметри транзистора
- •6.12. Основні типи транзисторів
- •5.14. Эквивалентная схема биполярного транзистора
- •4.Параметри та еквівалентні схеми біполярних транзисторів
- •4.1. Транзистор як лінійний чотириполюсник
- •4.2. Еквівалентна схема транзистора
- •4.3. Інші види еквівалентних схем.
- •4.4. Параметри транзистора при різних способах його увімкнення
- •4.5. Фізична еквівалентна схема транзистора
- •4.6. Способи визначення параметрів транзисторів.
- •4.7.Складений транзистор
5.14. Эквивалентная схема биполярного транзистора
Полученные в предыдущих разделах соотношения описывают взаимосвязь входных и выходных параметров биполярного транзистора в аналитической форме. Существует и другая форма представления этой взаимосвязи в виде эквивалентных схем, когда реальные процессы в нелинейных устройствах можно заменить на набор активных (источники тока и напряжения) и пассивных (резисторы, емкости) элементов, адекватно описывающих взаимосвязь входных и выходных параметров. На основе рассмотренных характеристик представим эквивалентную схему транзистора при включении по схеме с общей базой в следующем виде. Основные пассивные элементы (сопротивления rэ, rк, rб, емкости коллекторного СБ и эмиттерного СД переходов), активные элементы (генератор тока αIэ в коллекторной цепи, источник ЭДС μэкUк в эмиттерной цепи, отражающей обратную связь между эмиттером и коллектором) изображены на эквивалентной схеме (рис. 5.17).
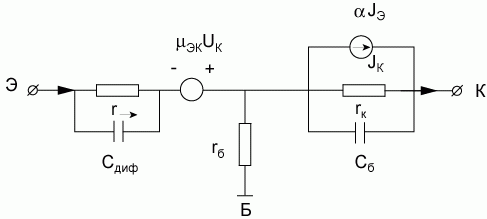
Рис. 5.17. Эквивалентная схема биполярного транзистора в схеме с общей базой
Приведенная эквивалентная схема справедлива для рассмотрения статических характеристик биполярного транзистора, а также для рассмотрения этих характеристик в области низких частот. Эта схема называется Т-образной эквивалентной схемой, отражает основные физические процессы, происходящие в транзисторе, и удобна для их анализа (рис. 5.18).
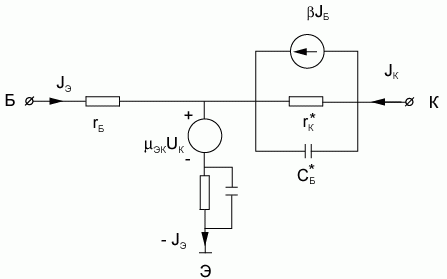
Рис. 5.18. Эквивалентная схема биполярного транзистора в схеме с общим эмиттером
Основные параметры эквивалентной схемы транзистора выражаются через конструктивно-технологические параметры следующим образом:

![]()
Величины коэффициентов α, rэ, rк, μэк для биполярного транзистора лежат в пределах:
α = 0,95÷0,995, rэ = 1÷10 Ом, rк = 10÷106 Ом, μэк = 10-3÷10-5.
Для биполярного транзистора в схеме с общим эмиттером эквивалентная схема выглядит аналогично.
Основные параметры эквивалентной схемы имеют тот же вид, что и в схеме с общей базой, кроме Ск* и rк*, равных: Ск* = Ск(β + 1), rк* = rк(β + 1).
Графический метод расчета громоздкий, неточный, исключает возможность аналитического анализа, используется для наглядного представления положения рабочей точки. Аналитический расчет производится только для переменных составляющих напряжений и токов. В этом случае транзистор заменяется эквивалентной схемой, которая представляет собой схему, состоящую из линейных пассивных и активных элементов. Эта схема справедлива только в режиме малого сигнала, т.е. когда связь между приращениями токов и напряжений линейна.
Существует два вида эквивалентных схем: физическая, отражающая процессы, протекающие в транзисторе, и формальная, в которой транзистор представляется в виде четырехполюсника.
Физическая эквивалентная схема составляется для переменных токов и напряжений, но при условии, что эмиттерный переход находится под прямым напряжением, а коллекторный переход - под обратным напряжением, а амплитуды сигналов таковы, что транзистор работает в линейном режиме.
Широко применяется Т – образная эквивалентная схема, показанная на рисунке 2.10.
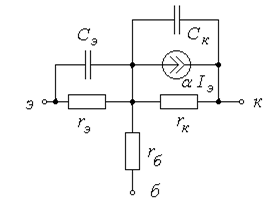
Рисунок 2.10 - Физическая эквивалентная схема биполярного транзистора
В этой схеме обозначено:
·
![]() -
дифференциальное сопротивление
эмиттерного перехода включенного в
прямом направлении. Обычно составляет
несколько десятков Ом.
-
дифференциальное сопротивление
эмиттерного перехода включенного в
прямом направлении. Обычно составляет
несколько десятков Ом.
·
![]() -
дифференциальное сопротивление
коллекторного перехода, включенного в
обратном направлении. Обычно составляет
несколько сотен кОм.
-
дифференциальное сопротивление
коллекторного перехода, включенного в
обратном направлении. Обычно составляет
несколько сотен кОм.
·
![]() -
объемное сопротивление базовой области.
База выполняется с минимальной примесью,
поэтому её сопротивление составляет
порядка нескольких сотен Ом.
-
объемное сопротивление базовой области.
База выполняется с минимальной примесью,
поэтому её сопротивление составляет
порядка нескольких сотен Ом.
·
![]() -
дифференциальный коэффициент передачи
по току при схеме включения с ОБ.
-
дифференциальный коэффициент передачи
по току при схеме включения с ОБ.
·
![]() -
емкость эмиттерного перехода, носит
диффузионный характер, часто влияние
этой емкости не учитывают даже на
сравнительно высоких частотах, т.к. она
шунтирована малым сопротивлением
.
-
емкость эмиттерного перехода, носит
диффузионный характер, часто влияние
этой емкости не учитывают даже на
сравнительно высоких частотах, т.к. она
шунтирована малым сопротивлением
.
·
![]() -
емкость коллекторного перехода является
барьерной емкостью, она оказывает
сильное влияние на частотные свойства
транзисторов.
-
емкость коллекторного перехода является
барьерной емкостью, она оказывает
сильное влияние на частотные свойства
транзисторов.
Формальная эквивалентная схема получила наибольшее распространение т.к. формальные параметры легко измеряются и приводятся в справочниках.
Рассмотрим формальную эквивалентную схему при включении транзистора с общим эмиттером (рисунок 2.11).
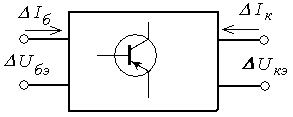
Рисунок 2.11 - Эквивалентная замена транзистора четырехполюсником
Если
за зависимые переменные принять
![]() и
и
![]() ,
то их можно выразить через независимые
переменные в виде уравнений
,
то их можно выразить через независимые
переменные в виде уравнений
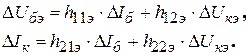 (2.12)
(2.12)
Значение
![]() –
параметров можно определить, проведя
опыт короткого замыкания на выходе и
опыт холостого хода на входе.
–
параметров можно определить, проведя
опыт короткого замыкания на выходе и
опыт холостого хода на входе.
Опыт
короткого замыкания на выходе
![]() ,
тогда из системы уравнений следует
,
тогда из системы уравнений следует
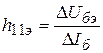 -
входное сопротивление транзистора при
схеме включения ОЭ;
-
входное сопротивление транзистора при
схеме включения ОЭ;
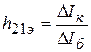 -
коэффициент передачи по току при схеме
включения ОЭ.
-
коэффициент передачи по току при схеме
включения ОЭ.
Опыт
холостого хода на входе
![]() ,
тогда из системы уравнений следует
,
тогда из системы уравнений следует
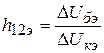 -
коэффициент внутренней обратной связи
при схеме включения с ОЭ;
-
коэффициент внутренней обратной связи
при схеме включения с ОЭ;
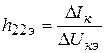 -
выходная проводимость при схеме включения
с ОЭ.
-
выходная проводимость при схеме включения
с ОЭ.
На основе приведенных уравнений можно построить эквивалентную схему транзистора в системе -параметров при включении с ОЭ (рисунок 2.12).
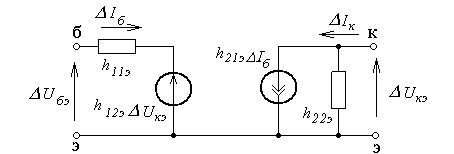
Рисунок 2.12 - Эквивалентная схема транзистора при включении с ОЭ
На практике численные значения параметров, если они не приведены в справочниках, определяют по статическим характеристикам транзистора. Параметры зависят от схемы включения транзистора, что отмечается третьим индексом "э", "б" или "к" соответственно для схем с ОЭ, ОБ или ОК. Покажем, как это делается, на примере схемы с ОЭ.
Параметры
![]() и
и
![]() определяют
по входным характеристикам транзистора
(рисунок 2.13).
определяют
по входным характеристикам транзистора
(рисунок 2.13).
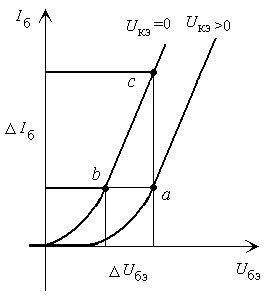
Рисунок 2.13 - Определение - параметров по входной характеристике
В
точке
![]() строят
характеристический треугольник. При
перемещении из точки
строят
характеристический треугольник. При
перемещении из точки
![]() в
точку
в
точку
![]() напряжение
напряжение
![]() ,
т.е.
,
т.е.
![]() ,
а входное сопротивление
,
а входное сопротивление
![]() равно
отношению катетов характеристического
треугольника
равно
отношению катетов характеристического
треугольника
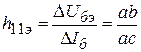 .
(2.13)
.
(2.13)
Коэффициент
внутренней обратной связи
![]() находится
при
находится
при
![]() (
(
![]() ),
что соответствует переходу из точки
в
точку
),
что соответствует переходу из точки
в
точку
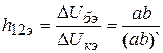 ,
(2.14)
,
(2.14)
где
![]() .
.
Параметры
![]() и
и
![]() определяют
по выходным характеристикам транзистора
(рисунок 2.14).
определяют
по выходным характеристикам транзистора
(рисунок 2.14).
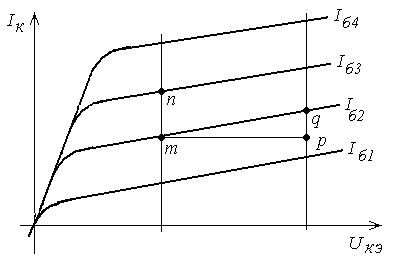
Рисунок 2.14 - Определение - параметров по выходным характеристикам
Для
того, чтобы в точке
![]() определить
параметр
,
строят характеристический треугольник
определить
параметр
,
строят характеристический треугольник
![]() .
Тогда катетами треугольника будут
приращения напряжения
.
Тогда катетами треугольника будут
приращения напряжения
![]() и
тока
и
тока
![]() ,
при выполнении условия
.
Численное значение параметра определяют
по формуле
,
при выполнении условия
.
Численное значение параметра определяют
по формуле
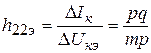 .
(2.15)
.
(2.15)
Для
определения параметра
через
точку
![]() проводят
вертикальную линию, которая пересекает
две соседних выходных характеристики.
Отрезок
проводят
вертикальную линию, которая пересекает
две соседних выходных характеристики.
Отрезок
![]() пропорционален
приращению тока
,
а приращение тока базы равно разности
токов, при которых сняты выходные
характеристики, то есть
пропорционален
приращению тока
,
а приращение тока базы равно разности
токов, при которых сняты выходные
характеристики, то есть
![]() ,
при этом
,
при этом
![]() .
Следовательно,
.
Следовательно,
![]()
 ,
(2.16)
,
(2.16)
где
![]() -
.
-
.
