Расчёты:
Таблица 8. Расчёт статистической вероятности события.
Интервалы времени ∆ti, ч. |
Отказы с момента начала эксплуатации |
|
Количество отказавших систем ni(∆ti) |
Статистическая
вероятность события
|
|
0-5 |
14 |
0,933 |
5-10 |
9 |
0,600 |
10-15 |
8 |
0,533 |
15-20 |
9 |
0,600 |
20-25 |
7 |
0,467 |
25-30 |
5 |
0,333 |
30-35 |
3 |
0,200 |
35-40 |
4 |
0,267 |
40-45 |
2 |
0,133 |
45-50 |
2 |
0,133 |
50-55 |
3 |
0,200 |
55-60 |
2 |
0,133 |
60-65 |
2 |
0,133 |
65-70 |
3 |
0,200 |
70-75 |
2 |
0,133 |
75-80 |
1 |
0,067 |
Для рассматриваемых систем управления справедлив экспоненциальный закон надежности:
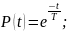
где Т=17,1 ч.
Рассчитаем значения теоретической функции вероятности безотказной работы P(t) по экспоненциальному закону надежности:
Результаты остальных расчётов сведём в таблицу 9.
Рассчитаем статистические значения вероятности отказа 𝑄̅(𝑡) и вероятность безотказной работы:
Результаты остальных расчётов сведём в таблицу 9.
Таблица 9. Результаты расчётов.
t, ч. |
|
|
P(t) |
5 |
0,933 |
0,067 |
0,746 |
10 |
0,600 |
0,400 |
0,556 |
15 |
0,533 |
0,467 |
0,414 |
20 |
0,600 |
0,400 |
0,309 |
25 |
0,467 |
0,533 |
0,230 |
30 |
0,333 |
0,667 |
0,172 |
35 |
0,200 |
0,800 |
0,128 |
40 |
0,267 |
0,733 |
0,095 |
45 |
0,133 |
0,867 |
0,071 |
50 |
0,133 |
0,867 |
0,053 |
55 |
0,200 |
0,800 |
0,040 |
60 |
0,133 |
0,867 |
0,029 |
65 |
0,133 |
0,867 |
0,022 |
70 |
0,200 |
0,800 |
0,016 |
75 |
0,133 |
0,867 |
0,012 |
80 |
0,067 |
0,933 |
0,009 |
По данным таблицы 9 построим графики и P(t).
Рисунок 4. Графики и P(t).
Проверим возможность аппроксимации функцией P(t) по критерию согласия Колмогорова. За меру расхождения между функциями и P(t) выбирается величина:
Выбираем наибольшую меру расхождения и проверяем возможность аппроксимации:
По величине 𝜆 с помощью табл. 10 определим вероятность p(𝜆).
Таблица 10. Вероятность p(𝜆).
Мера расхождения (𝜆) |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
Функция p(𝜆) |
1,0 |
1,0 |
0,99 |
0,86 |
0,54 |
0,27 |
0,11 |
0,04 |
0,012 |
0,003 |
Т.
к. мера расхождения
,
то функция
Поскольку условие
выполнено, то функцию
можно принять как рабочую (аппроксимирующую)
к функции
.