Общие требования к выполнению самостоятельной работы

Приступая к выполнению самостоятельной работы по математической статистике необходимо самостоятельно изучить теоретический материал и разобрать решение нулевого варианта, приведенного в образце выполнения самостоятельной работы. Только после этого рекомендуется приступать к решению самостоятельной работы.

Студент выполняет вариант самостоятельной работы, соответствующий последней цифре номера его зачетной книжки (цифре 0 соответствует номер 10). самостоятельной работа выполняется вручную в тетради, страницы которой имеют поля для замечаний преподавателя. Последовательность решения задач должна соответствовать последовательности заданий самостоятельной работы. Перед решением задачи необходимо переписать ее условие. Титульный лист выполняется на компьютере и оформляется по примеру, приведенному в приложении.

Образец выполнения самостоятельной работы

1. В результате исследования уровня экстраверсии в группе из 20 человек были получены следующие результаты:

Таблица 1

Показатели уровня экстраверсии

10	12	14	11	10	15	12	14	13	15
11	16	10	14	12	11	11	12	19	13

Для данной выборки:

а) построить вариационный ряд;

б) построить полигон частот;

в) вычислить выборочную среднюю, моду, медиану, разброс выборки, дисперсию и стандартное отклонение.

Решение. а) Находим , . Составим вариационный ряд в виде таблицы, где – выборочные значения, – частота данного значения (повторяемость в выборке):

Таблица 2

Расчётная таблица для решения задания 1

Уровень экстраверсии	10	11	12	13	14	15	16	19
Количество случаев	3	4	4	2	3	2	1	1

б) Для построения полигона вариационного ряда необходимо на плоскости отметить точки с координатами , где , – объем выборки и соединить в виде ломаной линии.

Рис. 1. Полигон вариационного ряда

в) Для вычисления выборочной средней используем формулу:

.

Наиболее часто (по 4 раза) встречаются значения 11 и 12, поэтому модой вариационного ряда будет .

Для нахождения медианы упорядочим исходную выборку значений:

Таблица 3

Упорядоченная выборка исходных данных

10	10	10	11	11	11	11	12	12	12
12	13	13	14	14	14	15	15	16	19

Так как четное количество данных, то медиана равна среднему арифметическому показателю между двумя центральными значениями:

.

Разброс выборки находим как разность между максимальной и минимальной величинами. Для данной выборки , , поэтому .

Для вычисления дисперсии удобно использовать следующую формулу:

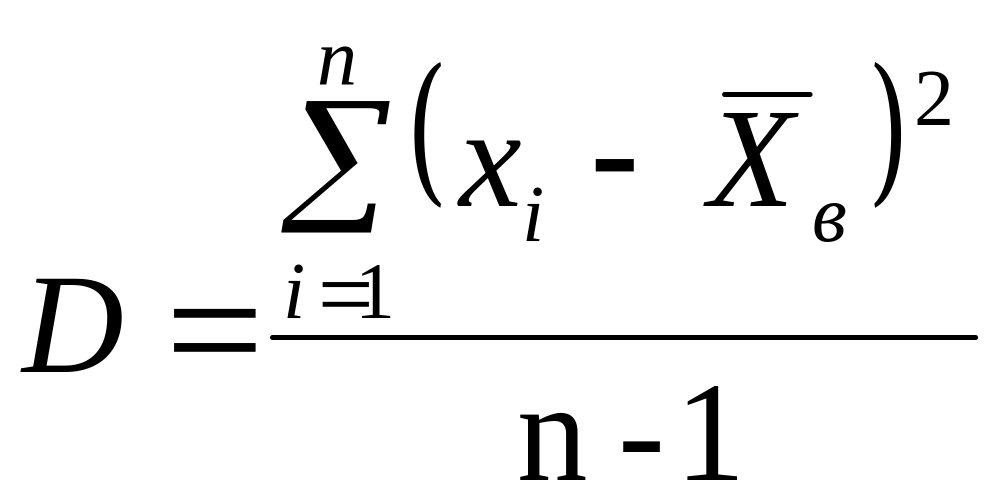
Учитывая, что среди значений есть повторяющиеся, вычисления можно записать в виде:

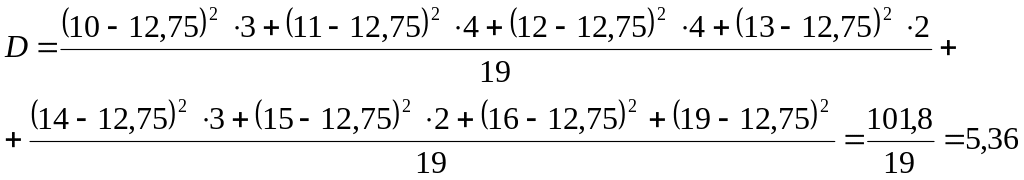
Стандартное отклонение

Ответ: ; ; ; ; ; .

2. У группы студентов был дважды измерен уровень интеллекта: в начале первого и второго учебного года. Данные представлены в таблице 4 ( ­и – результаты измерений в начале первого учебного года и второго соответственно). Можно ли сказать, что за год обучения интеллектуальный уровень студентов значимо изменился? Для решения задачи использовать - критерий Стьюдента.

Таблица 4

Исходные данные для задания 2

	100	102	109	111	105	123	115	125	111	102	109	115	123	120	114
	108	110	100	120	109	120	119	123	120	119	118	117	123	121	117

Решение. Сформулируем статистические гипотезы.

: разница между средними значениями интеллектуального уровня в начале первого и второго учебного года равна нулю.

: разница между средними значениями интеллектуального уровня в начале первого и второго учебного года отлична от нуля.

В таблице 5 приведены соответствующие экспериментальные данные и необходимые расчеты:

Таблица 5

Расчетная таблица для задания 2

№	Начальный срез	Конечный срез
1	100	108	8	64
2	102	110	8	64
3	109	100	-9	81
4	111	120	9	81
5	105	109	4	16
6	123	120	-3	9
7	115	119	4	16
8	125	123	-2	4
9	111	120	9	81
10	102	119	17	289
11	109	118	9	81
12	115	117	2	4
13	123	123	0	0
14	120	121	1	1
15	114	117	3	9
Сумма	1684	1744	60	800

Так как выборки связные и одинакового размера, то используется следующая формула - критерия Стьюдента:

, где

,

– разности между соответствующими значениями переменной и переменной , а – среднее этих разностей,

.

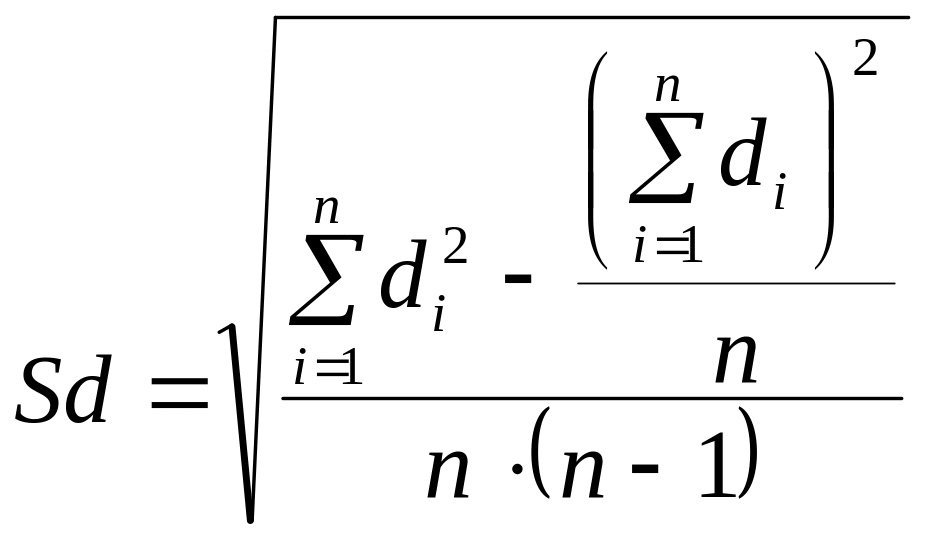Число степеней свободы определяется по формуле .

Вычислим ,

,

.

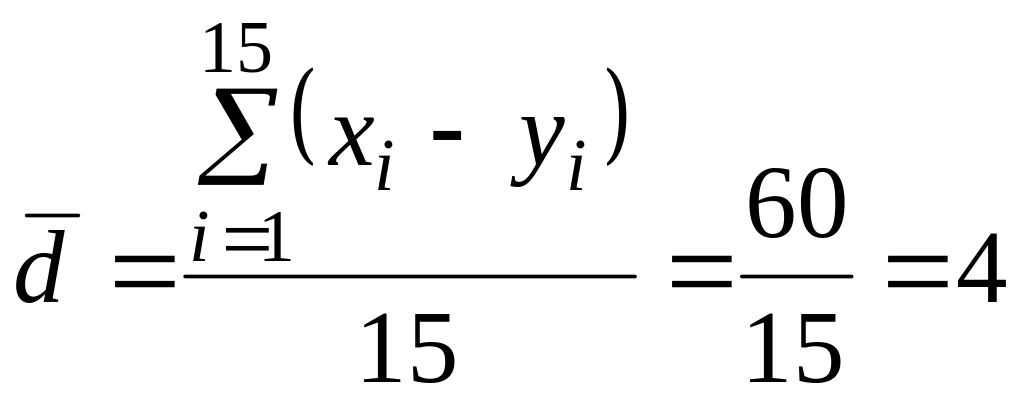Число степеней свободы равно , по таблице 14 Приложения 1 находим :

Отметим значения критерия на оси значимости (рисунок 3):

EMBED Equation.3

Рис. 2. Ось значимости для - критерия Стьюдента

Таким образом, на 5% уровне значимости гипотеза отклоняется и принимается гипотеза , то есть средние значения уровня интеллекта в начале первого и второго учебного года значимо различаются между собой.

3. В двух группах проводилось исследование нейротизма. Полученные значения приведены в таблице 6 ( ­и – результаты тестирования мальчиков и девочек соответственно). С помощью критерия Фишера определить достоверность различия дисперсий между показателями нейротизма у мальчиков и девочек.

Таблица 6

Исходные данные для задания 3

	19	8	12	9	16	15	15	12	22	15	14	12	8	16	20
	7	17	11	8	5	4	10	11	11	10	15	15	21	9	19

Решение. Сформулируем статистические гипотезы.

: дисперсии показателей двух групп статистически значимо не различаются.

: дисперсии показателей двух групп статистически значимо различаются.

Формула для подсчета эмпирического значения - критерия Фишера:

.

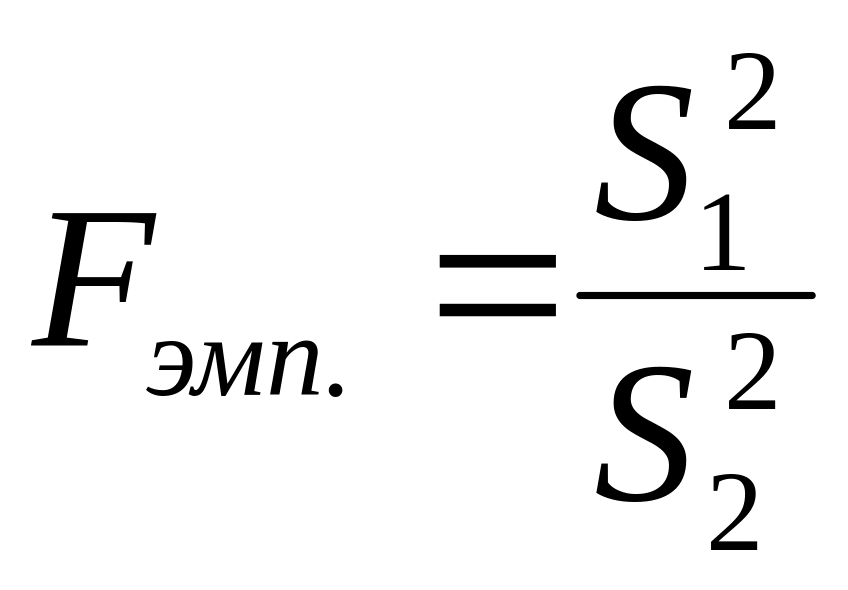В данной формуле – это всегда дисперсия с большим значением, а – с меньшим.

Рассчитаем дисперсии для переменных ­­и по формулам:

и .

,

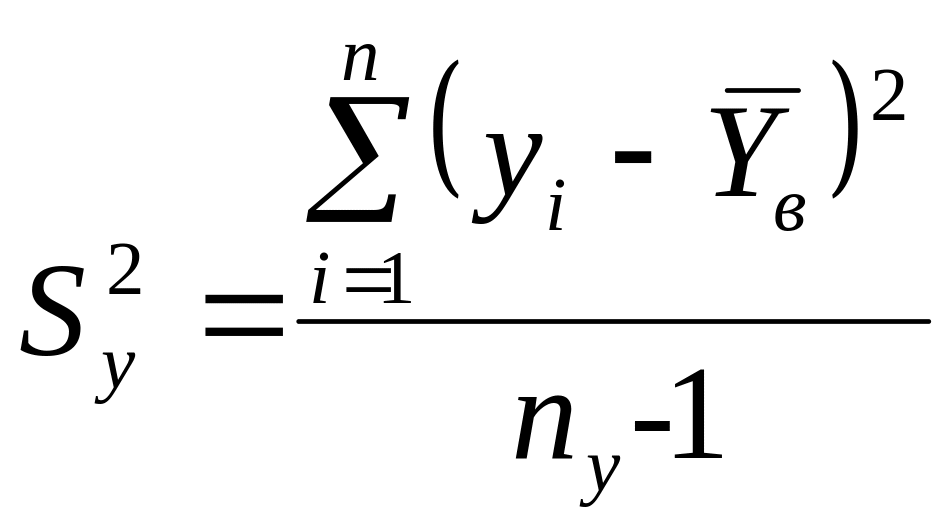значит .

Число степеней свободы в обоих случаях равно .

По таблице 15 Приложения 1 для - критерия находим :

Строим «ось значимости»:

Рис. 3. Ось значимости для - критерия

Наше эмпирическое значение лежит в зоне незначимости, поэтому мы принимаем гипотезу . Достоверность различий показателей дисперсии не обнаружена, т.е. по степени однородности такого показателя, как нейротизм, различий между мальчиками и девочками нет.

4. Оценить связь между показателями роста и веса с помощью коэффициента линейной корреляции Пирсона ( – рост, – вес приведены в таблице 7):

Таблица 7

Исходные данные для задания 4

	160	171	163	164	166	175	170	163	160	158	174	169	158	162	170
	58	68	50	59	68	63	54	51	50	49	70	65	48	52	63

Решение. Коэффициент линейной корреляции Пирсона вычисляется по формуле:

где 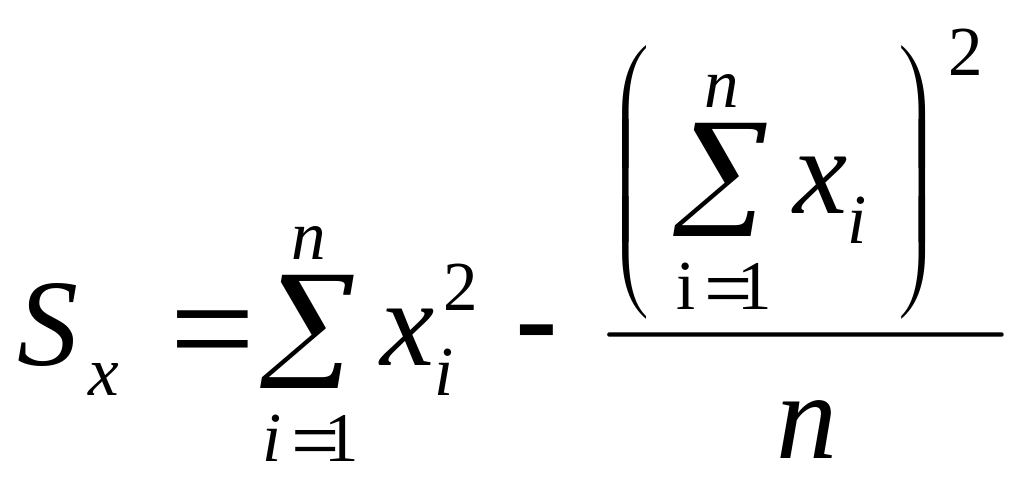и .

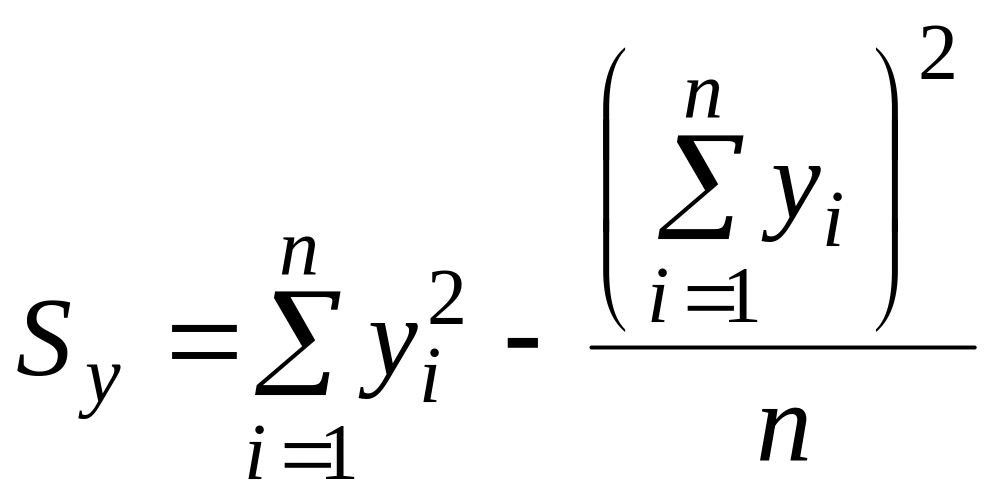Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем –1. Если коэффициент линейной корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными.

Если коэффициент линейной корреляции Пирсона положительный, то имеет место прямо пропорциональная зависимость, и наоборот.

Таблица 8

Расчетная таблица для задания 4

№ п/п	(рост)	(вес)
1	160	58	9280	25600	3364
2	171	68	11628	29241	4624
3	163	50	8150	26569	2500
4	164	59	9676	26896	3481
5	166	68	1088	256	4624
6	175	68	11025	30625	3969
7	170	84	9180	28900	2916
8	163	51	8313	26569	2601
9	160	50	8000	25600	2500
10	158	49	7742	24964	2401
11	174	70	12180	30276	4900
12	169	65	10985	28561	4225
13	158	48	7584	24964	2304
14	162	52	8424	26244	2704
15	170	73	10710	28900	3969
Сумма	2483	913	151840	411465	57237

,

,

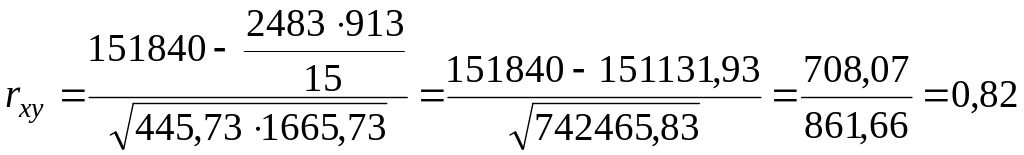
Вывод: связь между показателями роста и веса можно оценить как сильную положительную.

5. На выборке из 15 человек было проведено сравнительное исследование уровня интеллектуальной ригидности и уровня интеллекта ( – показатели интеллектуальной ригидности, – уровень интеллекта). Данные приведены в таблице 9. Необходимо найти уравнение линейной регрессии на .

Таблица 9

Исходные данные для задания 5

№ п/п
1	22	120	2640	484	14400
2	28	110	3080	784	12100
3	39	112	4368	1521	12544
4	33	115	3795	1089	13225
5	31	118	3658	961	13924
6	34	104	3536	1156	10816
7	15	116	1740	225	13456
8	38	110	4180	1444	12100
9	35	118	4130	1225	13924
10	32	118	3776	1024	13924
11	28	110	3080	784	12100
12	30	117	3510	900	13689
13	39	112	4368	1521	12544
14	32	115	3680	1024	13225
15	18	114	2052	324	12996
Сумма	454	1709	51593	14466	194967

Решение. Уравнение линейной регрессии имеет вид:

где ,

Для наших данных имеем:

,

,

,

.

Тогда искомое уравнение линейной регрессии имеет вид: .