Лабораторна робота №1
Тема: Наближені методи розв’язування задачі Коші для ЗДР і систем ЗДР
Методичні вказівки:
Для заданого варіанту завдання та вказаними викладачем методами знайти із заданою наперед точністю розв’язок задачі Коші для рівняння і для системи рівнянь. Стартові значення розв’язку, які необхідні для застосування багатокрокових методів, обчислити однокроковим методом, порядок точності якого узгоджений із порядком точності багатокрокового методу.
Усі інші значення розв’язку знаходити багатокроковим методом Адамса, Хеммінга, Ністрема або Мілна. Використані однокрокові та багатокрокові методи повинні бути узгоджені за порядком точності.
Параметри задачі задавати при вводі.
Вивести таблицю значень точного та наближеного розв’язків на сітці
,
абсолютну похибку наближеного розв’язку,
точність обчислень.Виконати обчислення за допомогою математичного пакета MATHCAD (функція rkfixed).
Описати алгоритм розв’язування задачі та зробити аналіз результатів.
Варіанти завдань
1.
а)
,
на відрізку [1;
1.6].
Точний
розв’язок:
.
б)
на відрізку [0; 0.6].
Точний
розв’язок:
,
.
2.
а)
,
на
відрізку
.
Точний
розв’язок
б)
на відрізку [4; 5].
Точний
розв’язок:
,
.
3.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний
розв’язок:
,
.
4.
а)
,
на відрізку [0; 0.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний розв’язок:
,
.
5.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний розв’язок:
,
,
.
6.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний розв’язок:
,
,
.
7.
а)
,
на відрізку [
].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний
розв’язок:
,
,
.
8.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний розв’язок :
,
,
.
9.
а)
,
на відрізку [0; 0.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний
розв’язок:
,
.
10.
а)
,
на відрізку [0; 0.8].
Точний
розв’язок :
.
б)
на відрізку [4; 4.8].
Точний
розв’язок :
,
.
11.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний
розв’язок:
,
,
.
12.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
Точний
розв’язок :
,
,
.
13.
а)
,
на відрізку [1; 1.8].
Точний
розв’язок:
.
б)
на відрізку
[0;
0,8].
Точний розв’язок:
,
,
.
14.
а)
,
на відрізку [0; 0.8].
Точний
розв’язок:
.
б)
на відрізку [0; 0.8].
б)
на відрізку [1; 4].
Точний
розв’язок:
.
15.
а)
,
Точний
розв’язок:
.
б)
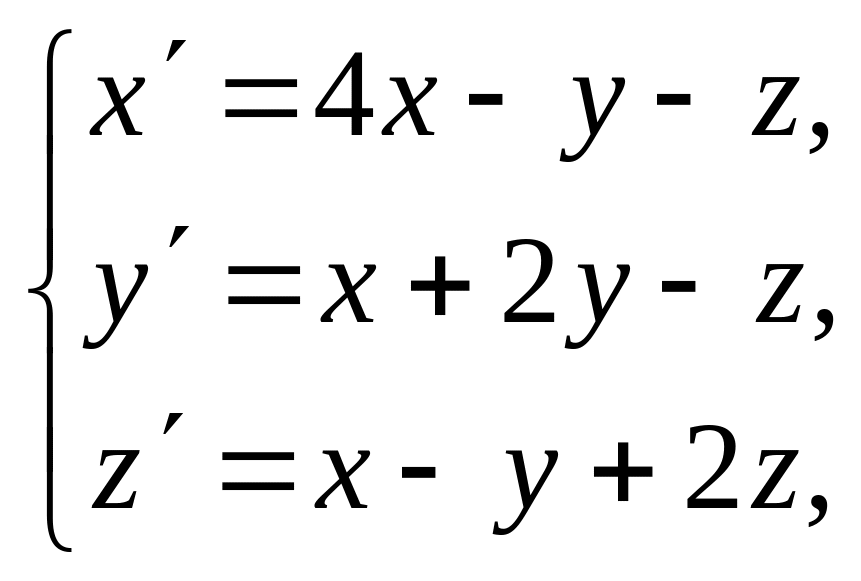
на відрізку [0; 0.8].
Точний
розв’язок:
,
,
.
16.
а)
,
на проміжку [2; 3.5].
Точний
розв’язок:
.
б)
Точний розв‘язок:
17.
а)
,
на відрізку [2; 4].
Точний
розв’язок:
.
б) на відрізку [1; 4].
Точний розв’язок: .
б)
на відрізку [0; 2.5].
Точние
значення розв’язку:
19.
а)
,
на відрізку [1; 4.5].
Точний
розв’язок:
.
б)
на відрізку [0; 1.5].
Точние
значення розв’язку:
20.
а)
,
на проміжку [2; 3.5].
Точний
розв’язок:
.
б)
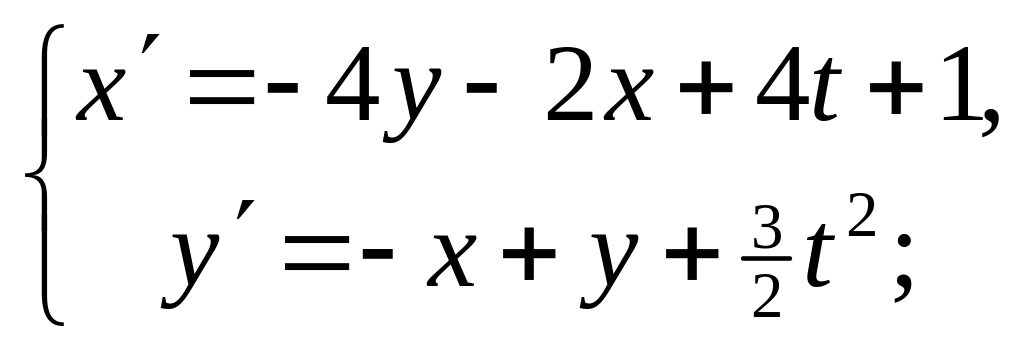
Точний розв‘язок:
21.
а)
,
на проміжку [1; 3].
Точний
розв’язок:
.
б)
на проміжку [0; 2].
Точний
розв’язок:
22.
а)
,
на проміжку [3; 5.5].
Точний
розв’язок:
.
б)
на проміжку
[1; 3.5].
Точний
розв’язок:
23.
а)
,
на проміжку [0; 1.5].
Точний
розв’язок:
.
б)
на
проміжку [0; 1].
Точний
розв’язок:
24.
а)
на проміжку
.
Точний
розв’язок:
.
б)
на
проміжку [0; 1].
Точний
розв’язок:
25.
а)
,
на проміжку
.
Точний
розв’язок:
.
б)
на проміжку [0; 1.5].
Точне
значення розв’язку:
26.
а)
,
.
на проміжку [1;2].
Точний
розв’язок:
.
б)
на проміжку [0;2].
Точний
розв’язок:
27.
а)
,
на відрізку [1; 3.5].
Точний розв’язок: .
б)
на проміжку [0; 1.5].
Точне
значення розв’язку:
28.
а)
,
на відрізку [1; 4].
Точний
розв’язок:
.
б)
на відрізку [0;2].
Точне
значення розв’язку:
29.
а)
,
на відрізку [
;
+1].
Точний
розв’язок:
.
б)
на відрізку [0;2].
Точний
розв’язок:
30. а) , на відрізку [1; 3].
Точний розв’язок: .
б)
на відрізку [0; 2].
Точне
значення розв’язку:
