
- •Лабораторний практикум
- •58012, Чернівці, вул.Коцюбинського, 2 §1. Числові методи розв’язування задачі Коші для звичайних диференціальних рівнянь
- •1.1. Постановка задачі
- •1.2. Метод Ейлера та його модифікації
- •1.3. Системи диференціальних рівнянь
- •1.4. Методи Рунге-Кутти
- •Формули методу Рунге-Кутти другого порядку
- •1.5. Про оцінку похибки наближеного розв’язку задачі Коші
- •1.6. Оcновні формули однокрокових методів
- •Формули методу Ейлера та його модифікацій Порядок
- •1.7. Багатокрокові методи розв’язування задачі Коші звичайних диференціальних рівнянь першого порядку
- •1.7.1. Методи Адамса
- •1.7.2. Метод Мілна
- •1.7.3. Метод Хеммінга
- •1.7.4. Неявні багатокрокові методи
- •1.7.5. Явні багатокрокові методи
- •1.8. Багатокрокові методи розв’язування систем звичайних диференціальних рівнянь
- •1.9. Розв’язування задачі Коші для систем диференціальних рівнянь першого порядку за допомогою функції rkfixed системи MathCad
- •Лабораторна робота №1
- •Варіанти завдань
- •§2. Лінійні крайові задачі
- •2.1. Постановка задачі
- •2.2. Побудова різницевої схеми
- •2.3. Методи прогонки для системи із тридіагональною матрицею
- •2.3.1. Метод правої прогонки
- •2.3.2. Метод лівої прогонки
- •2.3.3. Метод зустрічної прогонки
- •2.4. Розв’язування крайової задачі для диференціального рівняння n-ого порядку за допомогою функції sbval системи MathCad
- •Лабораторна робота №2
- •Задачі для здр 2-го порядку
- •Варіанти завдань
- •Список літератури
- •§1. Числові методи розв’язування задачі Коші для звичайних диференціальних рівнянь
- •§2. Лінійні крайові задачі
- •58012, Чернівці, вул.Коцюбинського, 2
Формули методу Рунге-Кутти другого порядку
Задамо
на відрізку
рівномірну сітку
![]() із кроком
із кроком
![]() Позначимо
через
Позначимо
через
![]() послідовні значення числового розв’язку
послідовні значення числового розв’язку
![]() в точках
в точках
![]() .
.
Для
двостадійного методу (s=2)
порядок точності
![]() і
найчастіше використовуються такі
значення коефіцієнтів:
і
найчастіше використовуються такі
значення коефіцієнтів:
|
|
Таблиця 2а. |
|
|
|
Таблиця 2б. |
||
|
|
|
|
|
|
|
|
|
-

Таблиця 2в.

Їм відповідають наступні формули:
 де
де
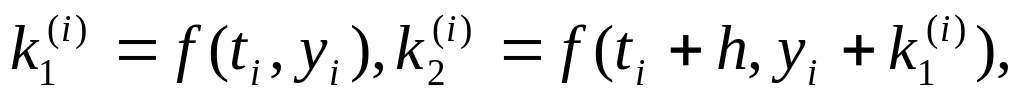 і=0,1,…,n-1
і=0,1,…,n-1 де
де
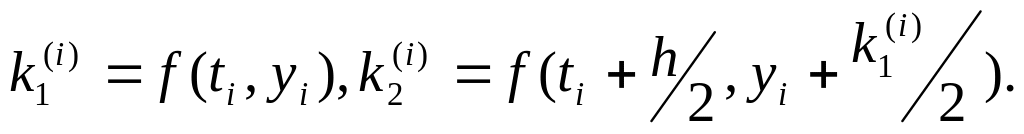
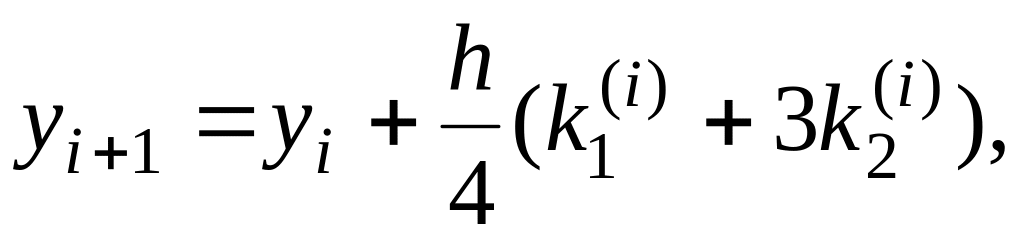 де
де


Формули методу Рунге-Кутти третього порядку точноссті
При s=3 найбільше застосовуються такі коефіцієнти і відповідні їм формули:
-
Таблиця 3а.




-

Таблиця 3б.
-
Таблиця 3в.
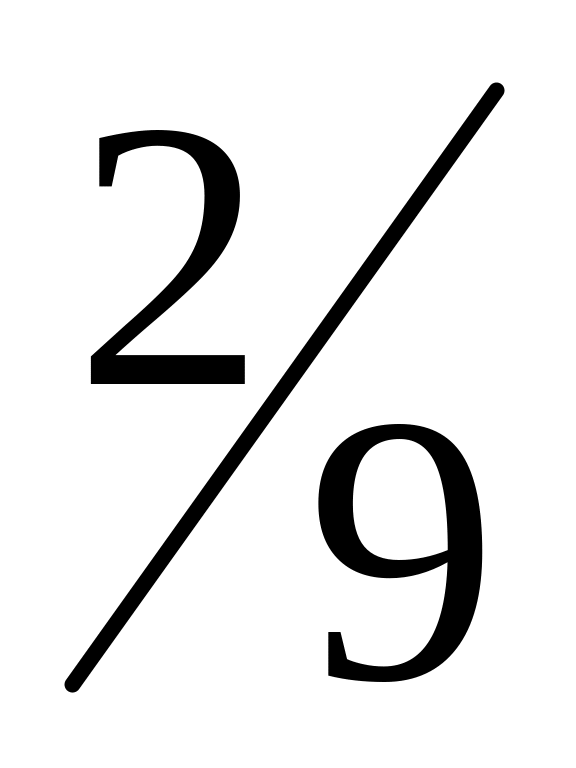
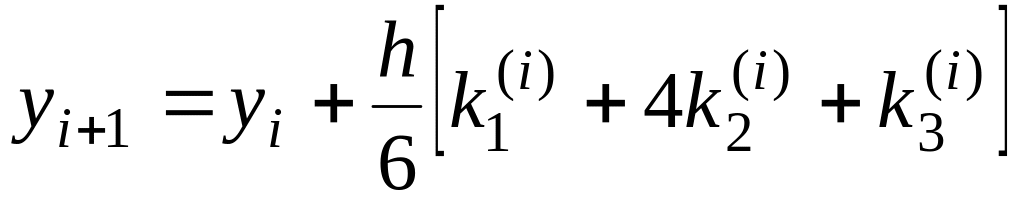 ,
де
,
де

 i=0,1,2,…,n-1.
i=0,1,2,…,n-1. де
де


 ,
де
,
де

Формули методу Рунге-Кутти четвертого порядку точності
В чотирьохстадійному методі найбільш уживані наступні коефіцієнти і формули:
-

Таблиця 6а.
Класичний метод Рунге–Кутти


-
Таблиця 6б. Метод “три восьмих ”





-
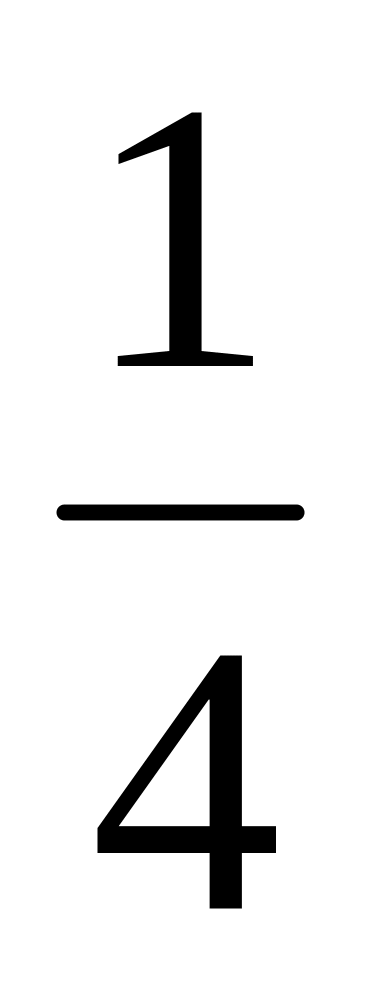
Таблиця 6в.
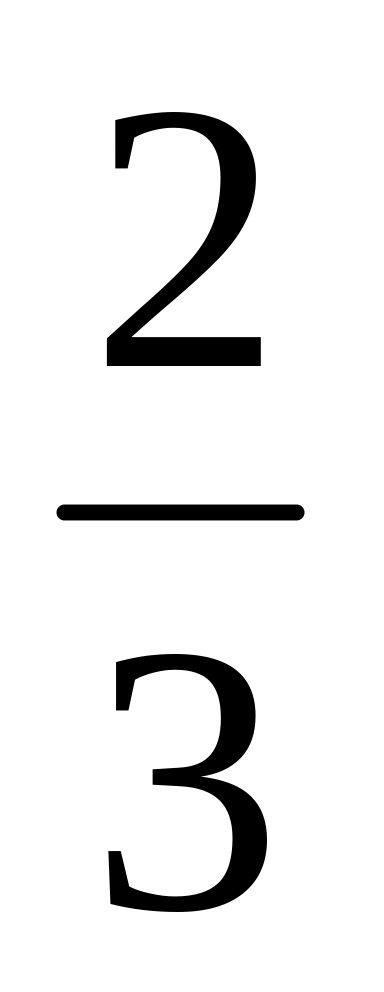
 ,
де
,
де


 i=0,1,2,...,n-1
i=0,1,2,...,n-1 ,
де
,
де

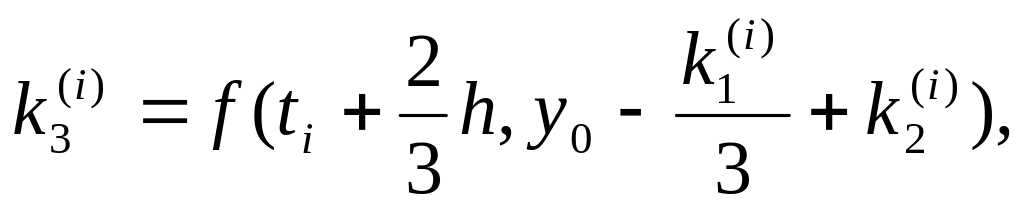
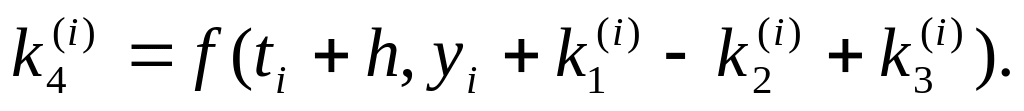
 ,де
,де


