Вопросы к практическому занятию
Сформулируйте правила проверки правильности построения эпюр поперечных сил и изгибающих моментов.
Запишите дифференциальные и интегральные зависимости, используемые при построении эпюр внутренних усилий при изгибе.
Какие сечения являются границами участков нагружения балок?
Почему положительные значения изгибающих моментов откладываются ниже, а отрицательные – выше базовой (нулевой) линии?
Обязательно ли определять опорные реакции для построения эпюр внутренних усилий в консольных балках?
Постройте эпюры внутренних усилий для консольных балок, схемы которых предложены преподавателем.
Практическое занятие 5 Построение эпюр внутренних усилий при изгибе двухопорных балок Теоретическая часть
Правила построения и проверки эпюр внутренних усилий при изгибе изложены в теоретической части к практическому занятию 4.
|
|
Рисунок 5.1 |
Рисунок 5.2 |
При конструировании двухопорных балок, как правило, используют два основных типа опорных закреплений. В шарнирно-подвижной опоре (рисунок 5.1) направление реакции R совпадает с направлением связи. В шарнирно-неподвижной опоре (рисунок 5.2) направление реакции неизвестно, поэтому пользуются двумя составляющими – вертикальной R и горизонтальной H, совпадающих с направлением связей. В частных случаях некоторые опорные реакции могут быть равны нулю; например, если балка нагружена только вертикальными усилиями, то горизонтальная составляющая опорной реакции равна нулю.
Пример 5.1
Построить эпюры внутренних усилий для двухопорной балки, нагруженной по всему пролету равномерно распределенной нагрузкой q (рисунок 5.3).
|
Рисунок 5.3 |
Решение
Определяем опорные реакции:
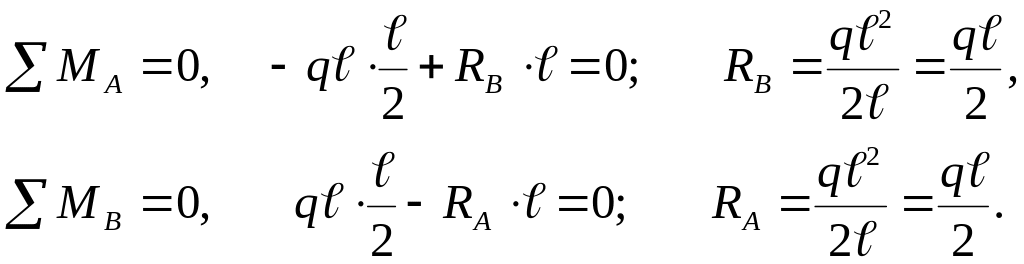
Проверка:
Балка имеет один участок нагружения, для которого определяем внутренние усилия.
|
Рисунок 5.4 |
:
в точке А:
z1=0;
;
в точке В:
z1=ℓ;
.
:
в точке А:
z1=0;
;
в точке В:
z1=ℓ;
.
Поскольку поперечная сила в пределах одного участка нагружения меняет знак с плюса на минус, то на эпюре изгибающих моментов в сечении, где поперечная сила равна нулю, будет экстремум (точка максимума). Определим, при каком значении координаты z1 поперечная сила Q(z1) обращается в ноль. Для этого приравняем к нулю уравнение поперечной силы Q(z1)=0 для рассматриваемого участка:
.
Определим значение изгибающего момента M(z1) при z1=ℓ/2:
.
По полученным данным строим эпюры Q(z1) и M(z1). Эпюру изгибающего момента строим на растянутых волокнах.
Ввиду нелинейности эпюры M(z) выполним интегральную проверку по формуле (4.2):
,
где ΩQAB – площадь эпюры поперечных сил на рассматриваемом участке АВ; поскольку на рассматриваемом участке часть эпюры лежит ниже базовой линии, ее площадь полагаем отрицательной, а площадь части эпюры, расположенной выше базовой линии – положительной;
МВ – значение изгибающего момента в точке В – конечной точке рассматриваемого участка;
МА – значение изгибающего момента в точке А – начальной точке рассматриваемого участка.
Для середины участка нагружения сечения С, где z1=ℓ/2, интегральная проверка выполняется по тем же правилам:
