Порядок выполнения работы

1. Включить осветитель поляриметра (см. рис 3.9) в сеть.

2. Открыть камеру поляриметра и убедиться, что кювета 2 с раствором вынута.

3. Перемещая окуляр 5, установить ясное видение разделяющих линий тройного поля зрения, шкалы и нониуса.

4. Вращая рукоятку 6, добиться равномерного затемнения трех частей поля зрения; при этом шторка на камере прибора должна быть закрыта.

5. Снять отсчеты по левому и правому нониусам n₀′ и n₀″.Опыт повторить три раза и найти средние значения .

6. Поместить кювету с раствором сахара известной концентрации в поляриметр.

7. Вращая рукоятку 6, снова добиться равномерного затемнения трех частей поля зрения. Снять отсчеты по левому и правому нониусу n₁′ и n₁″^'. Измерение повторить три раза. Найти средние значения .

8. Измерения повторить три раза с раствором неизвестной концентрации. Найти средние значения . Все отсчеты привести к одинаковой длине кювет, учитывая прямо пропорциональную зависимость длины кюветы и показаний поляриметра.

9. Определить углы вращения плоскости поляризации по формулам

и , результаты занести в таблицу.

10. Рассчитать[₀] = 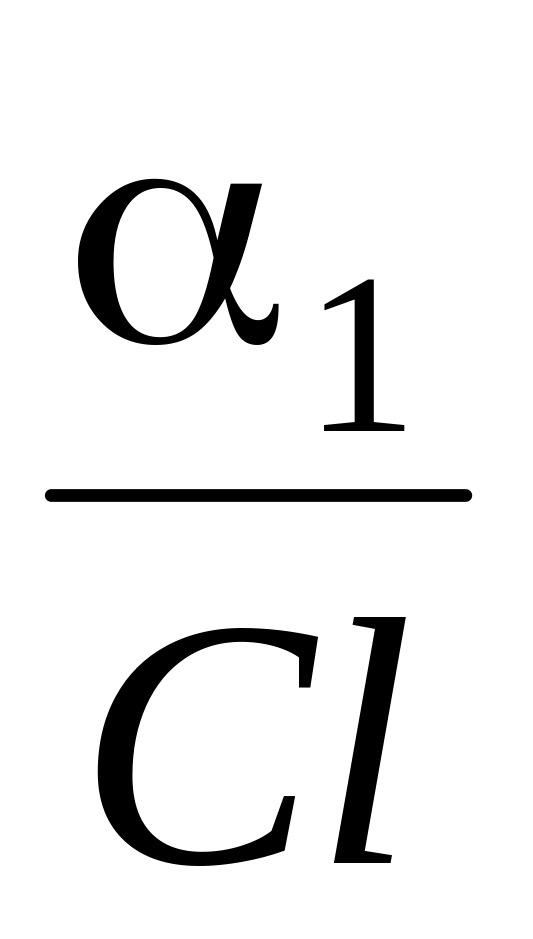, С_x = .

Концентрация раствора С, %	Длина кюветы l, см	Отсчеты по нониусу				Угол поворота  ,…	Удельное вращение [0], радм2кг
		n		n

Контрольные вопросы

1. Какова природа света?

2. В чем заключается явление поляризации света?

3. Что такое естественный и поляризованный свет?

4. Виды поляризации. Какую волну называют плоскополяризованной?

5. Каковы способы получения поляризованного света?

6. В чем заключается явление двойного лучепреломления?

7. Сформулируйте законы Малюса, Брюстера.

8. Какие вещества называются оптически активными?

9. Как определяется угол поворота плоскости поляризации твердыми веществами и растворами?

4. Взаимодействие излучения с веществом

4.1. Дисперсия света Основные понятия

Под дисперсией света подразумеваются явления, обусловленные зависимостью показателя преломления вещества от длины световой волны. Свет разных длин волн (разного цвета) преломляется не одинаково на границе двух прозрачных веществ. Для определенности будем рассматривать преломление на границе вакуум - данное вещество, т. е. говорить о зависимости от длины волны  абсолютного показателя преломления вещества n. В этом случае показатель преломления данного вещества является функцией длины волны

. (4.1)

Дисперсией вещества называется величина, определяющая быстроту изменения показателя преломления n с длиной волны. Если двум длинам волн ₁ и ₂ соответствуют значения показателя преломления n₁ и n₂ , то средняя дисперсия вещества D на участке длин волн от ₁ до ₂ определяется соотношением

.

Переход к бесконечно малому интервалу длин волн позволяет определить дисперсию вещества вблизи данной длины волны через производную, т.е.

. (4.2)

Для всех прозрачных веществ показатель преломления монотонно возрастает с уменьшением длины волны. Это говорит о том, что в прозрачных веществах фиолетовые лучи преломляются сильнее зеленых, а зеленые - сильнее красных.

На рис. 4.1 приведены зависимости n от  для стекла 1 (легкий флинт), кварца 2 и флюорита 3. Из рисунка видно, что показатель преломления особенно сильно возрастает с уменьшением длины волны в области коротких волн. Этот вывод соответствует равенству (4.2), т. е. дисперсия прозрачных веществ возрастает по численному значению с уменьшением длины волны. Такая дисперсия называется нормальной.

Р азличная преломляемость лучей разного цвета позволяет разложить сложный цвет на его монохроматические составляющие. Такой опыт был впервые проведен в 1672 г. Ньютоном. Схема опыта поясняется на рис. 4.2, заимствованном из книги Ньютона «Оптика».

Л уч света от Солнца S проходит через малое отверстие F в ставне окна; преломленный призмой Р луч попадает на лист белой бумаги M. При этом круглое отверстие в ставне F растягивается в окрашенную полоску АВ. Красный конец полоски. В соответствует менее преломившемуся лучу, а фиолетовый край полоски А - более преломившемуся лучу. Цветную полоску АВ Ньютон назвал спектром.

Свет Солнца дает сплошной спектр с непрерывным переходом одних цветов в другие. Раскаленные газы и пары металлов дают линейчатый спектр, состоящий из отдельных цветных полос, разделенных темными промежутками. Аналитический вид функции (4.1), определяющей зависимость показателя преломления n от длины волны  , приближенно можно представить в виде

,

где А и В - постоянные величины.

В этом случае дисперсию вещества можно описать выражением

.

Влияние вещества на распространение света обусловлено взаимодействием света с атомами и молекулами, из которых вещество состоит. Это взаимодействие ведет к изменению скорости света и определяет значение абсолютного показателя преломления вещества

,

где - с - скорость света в вакууме, м/с; v - скорость света в среде, м/с.

Теоретическое обоснование закономерностей дисперсии можно получить на основании макроскопической электромагнитной теории Максвелла и электронной теории Лоренца.

По теории Максвелла следует, что абсолютный показатель преломления среды

,

где  - диэлектрическая проницаемость среды;  - магнитная проницаемость среды.

В оптической области спектра для всех веществ 1, поэтому

. (4.3)

Значения n, получаемые из этого выражения, не согласуются с опытными данными. Трудности объяснения дисперсии света на основе теории Максвелла устраняются теорией Лоренца, по которой дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны (световой). Рассмотрим однородный диэлектрик, предположив, что дисперсия света является следствием зависимости  от частоты  световых волн.