2. Дифракция света

Основные понятия

Дифракция света – это физическое явление огибания световыми волнами преград, соизмеримых с длиной волны, например, при прохождении малых отверстий или вблизи малого непрозрачного экрана. Явление дифракции объясняется на основе принципа Гюйгенса – Френеля, в котором по Гюйгенсу каждая точка фронта волны является центром вторичных волн, а огибающая этих волн повторяет форму фронта волны источника и определяет положение фронта волны в пространстве. Так, фронт плоской волны (источник света далеко и лучи от него параллельны) остается плоскостью, а фронт сферической волны (источник точечный, близко расположен) - сферой. Френель утверждение Гюйгенса наполнил физическим смыслом, дополнив его идеей интерференции вторичных волн: световая волна – это результат наложения когерентных вторичных волн, излучаемых мнимыми источниками фронта волны.

Д ля выяснения результата интерференции вторичных волн Френель применил прием, получивший название метода зон Френеля. Согласно этому методу видимый фронт волны делится на участки (для сферических волн это кольцевые зоны, для плоских – прямоугольные полоски). Размеры этих зон таковы, что расстояния от краев соседних зон до наблюдателя отличаются на /2. Способ построения зон Френеля для сферического фронта схематически показан на рис 2.1.

Чтобы найти амплитуду световой волны в точке М (наблюдатель) от источника S, заменим ее действие мнимыми источниками фронта волны Ф. Разобьем фронт волны на зоны Френеля, для этого проведем с центром в точке М сферы радиусами где r₀ – расстояние от центра фронта волны до точки наблюдения. Тогда расстояния МР₀, МР₁, МР₂, . . . .МР_m будут отличаться на , поэтому световые волны до точки М от соседних зон приходят в противоположных фазах и при наложении ослабляют друг друга. Суммарная амплитуда в точке М

. (2.1)

Можно доказать, что площади зон Френеля не зависят от номера зоны при условии  r₀,  a (a – радиус видимого фронта волны), а амплитуды световых волн связаны неравенством А₁  А₂  А₃ А₄ . . .

Для видимого диапазона световых волн и реальных размеров (а  r₀  10 см) фронта волны можно считать амплитуду света от зоны как среднее арифметическое примыкающих зон, тогда

.

Из этого выражения следует, что интенсивность света в точке М зависит от амплитуды только первой зоны, а так как она мала, то можно считать, что свет распространяется в пространстве только по каналу размерами первой зоны (r_m 10^-4 м), т.е. прямолинейно. При менее точном приближении можно считать амплитуды волн от зон равными и тогда по выражению (2.1) условие максимума дифракции Френеля (точечный источник) соответствует нечетному, а условие минимума – четному числу зон Френеля на видимом фронте волны.

Дифракцию в параллельных лучах, или дифракцию плоской волны рассмотрел И. Фраунгофер. Для наблюдения дифракции Фраунгофера нужно параллельный пучок света после дифракции на препятствии направить на собирающую линзу, в фокальной плоскости которой локализуется дифракционная картина.

Рассмотрим дифракцию Фраунгофера от узкой щели (рис 2.2). Пусть плоская световая волна падает нормально на щель MN, ширина которой a   (MN - фронт падающей волны, MK – фронт волны после дифракции,  - угол дифракции). Если установка находится в воздухе (n = 1), то оптическая разность хода крайних лучей

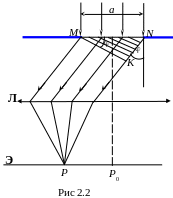 = NK = asin . (2.2)

Р азобьем видимую часть фронта волны на зоны Френеля – полоски, параллельные ребру щели М. Число зон Френеля будет равно числу отрезков по на отрезке NK, т.е. . И если это число будет четным, , то в точке Р на-блюдается минимум, а если нечетным , то максимум. Решая совместно формулу (2.2) и два последних равенства, получим соответственно условие минимума (2.3) и максимума (2.4) дифракции на одной щели:

(k = 1,2,3…), (2.3)

(2.4)

(число k определяет порядок дифракции).

При  = 0 щель действует как одна зона Френеля, и в точке Р₀ будет наблюдаться центральный дифракционный максимум. Согласно формулам (2.3) и (2.4) , угол  зависит от , поэтому при наблюдении дифракции белого света картина на экране кроме центрального максимума будет радужно окрашенной.

При дифракции на одной щели белого света спектр получается расплывчатым и нет четкого разделения различных длин волн.

Четкую картину разложения света можно получить при прохождении света через одномерную дифракционную решетку. Дифракционная решетка – система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Дифракционная картина на решетке определяется как результат взаимной интерференции световых волн, идущих от разных щелей.

Р ассмотрим дифракционную решетку (рис 2.3). На рисунке показаны только две щели MN и KL, их ширина a, b – ширина непрозрачных участков, (a, b  ), d = a + b называется постоянной (периодом) решетки,  - угол дифракции, KB – разность хода от двух щелей (она будет постоянна в пределах дифракционной решетки)

. (2.5)

Очевидно, что в направлениях, в которых ни одна из щелей не распространяет свет (минимум), он не будет распространяться от всех щелей, т.е. главные минимумы дифракционной решетки совпадают с минимумами от одной щели:

. (2.6)

Между главными минимумами располагаются дополнительные минимумы, их число зависит от общего числа щелей решетки N, а их условие определяется формулой

.

При пропускании света действие одной щели будет усиливаться действием другой, поэтому условие главных максимумов выразится как

. (2.7)

Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между главными соседними максимумами, тем интенсивнее и более острыми будут максимумы, тем точнее их можно идентифицировать.

Большой интерес представляет дифракция на пространственных периодических структурах. Такими структурами являются кристаллы, в которых атомы (ионы) расположены в строгом порядке, образующем трехмерную решетку с постоянным расстоянием между узлами a, b, c. Отдельным элементом, препятствующим электромагнитному излучению, является узел решетки. Для того, чтобы обнаружить дифракцию, необходима соразмерность щелей и преград с длиной падающей волны. Поэтому видимый свет, длина волны которого лежит в пределах (4 – 7,6)10^-7 м, не может дифрагировать на решетке кристалла, параметры решетки которого имеют размеры порядка 10^-10 м.

Впервые идею использования для наблюдения дифракции на кристаллических структурах рентгеновского излучения (  10^-12 – 10^-8 м) была высказана М. Лауэ; он же предложил схему опыта (рис. 2.4).

Р ентгеновские лучи попадают на кристалл С, дифрагируют, дифракционные максимумы фиксируются на фотопленке P. Наблюдаемая дифракционная картина может быть использована для двух целей: для определения типа кристаллической решетки и ее параметров, если известна длина волны рентгеновского излучения и для измерения длины волны излучения, если известны тип решетки и ее параметры.

С пособ расчета длины волны был дан Ю. В. Вульфом и У. Г. и У. Л. Брэггами и называется методом Вульфа – Брэггов. Авторы метода предположили, что дифракция рентгеновских лучей является результатом отражения от системы параллельных кристаллических плоскостей кристаллической решетки (рис 2.5). Рассмотрим две такие плоскости, отстоящие друг от друга на расстояние d.

Рентгеновские лучи падают на кристалл под углом скольжения . Крайние лучи параллельного пучка отражаются от узлов А и В соседних плоскостей (АС – фронт падающей волны, АD – фронт отраженной волны). Падающие 1, 2 лучи и отраженные 1 и 2 - когерентны и при интерференции дадут либо максимум, либо минимум.

Из рисунка видно, что разность хода 1 и 2 лучей определяется отрезками СВ и BD, которые равны между собой, а их величина равна d sin (из треугольника АСВ), т.е.  = 2dsin .

Для максимума  = k (k = 1,2,3…), следовательно:

2d sin  = k (k = 1,2,3…). (2.8)

Соотношение (2.8) называется формулой Вульфа – Брэггов, метод определения длины волны рентгеновского излучения по этой формуле лежит в основе рентгеноспектрального анализа.

Лабораторная работа. 2

ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ ИЗЛУЧЕНИЯ

РАЗЛИЧНЫМИ МЕТОДАМИ

Задание 1

Цель работы: при помощи дифракционной решетки определить длину волны спектров первого и второго порядка.

П риборы и принадлежности: источник света, дифракционная решетка, щель, шкала с делениями.

Методика эксперимента

Общий вид установки для эксперимента представлен на рис.2.6. По массивной линейке 1 передвигается экран 2, в котором вырезана щель 3. На экран нанесена шкала 4, нуль которой совмещен с серединой щели. К передней части линейки прикреплена рамка 5, в которую вкладывается дифракционная решетка. Для определения длины волны по формуле (2.7)

(2.9)

н еобходимо знать угол .

Рассмотрим схему образования симметричного изображения щели на экране (рис. 2.7): Д.Р. – дифракционная решетка;

Э – экран с симметрично расположенными спектрами.

По рисунку , т.к. l  x, угол  мал, тогда tg  sin. Формула (2.9) преобразуется . (2.10)

Порядок выполнения работы

1. Включить источник света.

2. Установить экран на такое расстояние, чтобы на нем получилось отчетливое изображение спектров первого и второго порядка.

3. Передвигая экран по линейке, устанавливать экран так, чтобы красные и синие (зеленые и фиолетовые) линии спектров первого и второго порядков совпадали с заданными расстояниями x₁ = 10мм и x₂ = 20 мм, каждый раз измеряя расстояние l. Данные занести в таблицу.

x, мм	k	lкр, мм	lсин, мм	lфиол, мм	кр, нм	син, нм	фиол, нм
10	1
	2
20	1
	2

4. Вычислить длины волн по формуле (2.10).

5. Рассчитать абсолютную и относительную погрешности для одной из найденных длин волн.

Задание 2

Цель работы: определить длины волн видимого спектра при помощи гониометра.

Приборы и принадлежности: источник света, гониометр, дифракционная решетка.

Методика эксперимента

Гониометр является оптическим контрольно-измерительным прибором, позволяющим производить измерения углов.

Основные элементы установки показаны на рис. 2.8.

Свет от источника S через диафрагму Д и собирающую линзу Л попадает на щель Щ коллиматора К, затем на дифракционную решетку ДР. За решеткой свет дифрагирует и картина дифракции, состоящая из центральной белой полосы и окрашенных (максимумы) линий, наблюдается через зрительную трубу ЗТ. В поле окуляра О видны одиночные линии дифракционного спектра. Углы дифракции  измеряются измерительным устройством гониометра – отсчетным микроскопом.

Порядок выполнения работы

1. Включить в сеть кабель гониометра и источник света.

2. Вращением зрительной трубы добиться совмещения перекрестия сетки окуляра с фиолетовой линией видимого спектра слева от центрального дифракционного максимума. Взять отсчет N₁ по отсчетному микроскопу.

3. Повернуть зрительную трубу до совмещения фиолетовой линии справа от центрального максимума; перекрестием сетки окуляра взять отсчет N₂.

4. Повторить эксперимент для других линий видимого спектра.

5. Данные занести в таблицу.

Цвет линий	Отсчет слева N1	Отсчет справа N2	N2 – N1		sin	d, мм	, нм
фиолетовый							4,35810-8м

6. Определить углы дифракции для каждой линии .

7. Используя формулу (2.9), по данным для фиолетовой линии рассчитать постоянную дифракционной решетки.

8. Рассчитать длины волн для других линий спектра (по той же формуле), считая d известным.

9. Рассчитать для одной длины волны абсолютную и относительную погрешности измерений. Записать для этой длины волны результат измерений.

Задание 3

Цель работы: определить длину волны рентгеновского излучения.

Приборы и принадлежности: компаратор, рентгенограмма, рентгеновская камера.

Методика эксперимента

Одним из методов определения длины волны рентгеновского излучения является метод порошка. Сущность метода состоит в следующем. Пучок монохроматических рентгеновских лучей направляется на образец с известной структурой, а следовательно, с известным межплоскостным расстоянием. Образец в виде порошка наносится на стеклянную нить или спрессован в цилиндрик диаметром 0,2 – 0,8 мм и помещен в специальную рентгеновскую камеру. Чаще всего рентгеносъемку проводят в цилиндрических камерах (схема съемки на рис. 2.9).

О бразец К укрепляется в центре камеры. По цилиндрической поверхности камеры располагается фотопленка. Первичный пучок рентгеновских лучей направляется на исследуемый образец через узкую щель ав и после дифракции оставляет на пленке следы в виде кривых линий (рис.2.10). Независимо от задачи исследования в любом случае необходимо точно определить положение линий на рентгенограмме (фотографии картины дифракции), т.е. точно определить их интенсивность и углы отражения. Важную роль в получении четких рентгенограмм играет подбор излучения, так как характеристическое излучение рентгеновских трубок неоднородно, поэтому излучение подбирают так, чтобы на рентгенограмме было как можно меньше слабых линий, или используют специальные фильтры, поглощающие мешающие длины волн.

Углы определяют по расстоянию между симметричными линиями 2l на рентгенограмме и, зная межплоскостное расстояние кристаллической решетки образца и используя формулу Вульфа – Брэггов (2.8), рассчитывают длину волны рентгеновского излучения:

(k =1,2,3…). (2.11)

Порядок выполнения работы

1. Познакомиться с устройством рентгеновской камеры и способом закладки в нее рентгеновской пленки.

2. Поместить пленку на компаратор, включить осветитель компаратора.

3. Промерить расстояние между указанными линиями рентгенограммы, записать в таблицу.

4. Рассчитать углы отражения в градусах по формуле (где R – радиус рентгеновской камеры), записать в таблицу.

Номер линии	d, мм	k		sin	, м	,м

5. По углам найти sin.

6. Рассчитать по формуле (2.11) длину волны, найти ее среднее значение.

7. Рассчитать абсолютную и относительную погрешности измерений.

Контрольные вопросы

1. Что такое дифракция света? В чем заключается принцип Гюйгенса – Френеля?

2. Что такое зоны Френеля? Как строятся зоны Френеля?

3. При каких условиях наблюдается дифракция Френеля, дифракция Фраунгофера?

4. Постройте ход лучей при дифракции от одной щели. Каковы условия усиления и ослабления света в этом случае?

5. Постройте ход лучей при дифракции на дифракционной решетке. Каковы условия усиления и ослабления света в этом случае?

6. Как определить наибольший порядок спектра дифракционной решетки?

7. Как изменится дифракционная картина при удалении экрана от решетки?

8. Почему при использовании белого света только центральный максимум белый, а боковые максимумы радужно окрашены?

9. Почему нельзя наблюдать дифракцию видимого света на кристаллах?

10. Какие практические применения имеет формула Вульфа – Брэггов?