914

Рисунок 25 . Вес тела в ускоренно движущемся лифте. Вектор ускорения направлен вертикально вверх. Вес тела приблизительно в два раза превышает по модулю силу тяжести (двукратная перегрузка).

МЕХАНИКА. (для 3-х семестров).

Лекция № 1.

Обработка результатов эксперимента.

1. Измерения и погрешности измерений

Выполнение лабораторных работ связано с измерением физических величин. Измерением называют определение значения физической величины опытным путем с помощью специальных технических средств (приборов, установок, мер). Численные значения физических величин, полученные при измерениях, являются результатами измерений. Однократное определение физической величины называется наблюдением.

Измерения делят на прямые и косвенные. Прямыми называются измерения, при которых искомое значение величины определяется путем отсчета по шкале измерительного прибора или сравнения с мерой. Например, время измеряется секундомером, длина - с помощью линейных мер, сила тока - амперметром и т.д.

При косвенных измерениях значение физической величины вычисляют по результатам прямых измерений других величин, связанных с искомой величиной функциональной зависимостью (расчетной формулой). Например, мощность электрического тока P можно вычислить по результатам прямых измерений силы тока I и напряжения U, пользуясь формулой .

При всяком измерении неизбежны погрешности. Погрешность - это отклонение результата измерения от истинного значения измеряемой величины. Истинным является такое значение физической величины, которое идеальным образом отражает свойства изучаемого объекта.

Погрешность может быть представлена в абсолютной и относительной формах. Абсолютной погрешностью измерения а физической величины а называют разность между результатами измерения а и истинным значением измеряемой величины а₀:

.

Относительная погрешность  показывает, какую часть (или какой процент) абсолютная погрешность а составляет от истинного значения а₀.

или .

Погрешность любого измерения складывается из двух составляющих - систематической и случайной.

Систематическая погрешность - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематическая погрешность вызвана техническим несовершенством средств измерений и отсчета по их шкалам, использованием для вычислений приближенных формул, неточных данных и т.д.

Случайная погрешность - составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях данной величины. Эта составляющая обусловлена, например, случайными процессами, происходящими в окружающей среде, в измерительном приборе, а также субъективными причинами. К случайным примыкают грубые погрешности измерения (промахи), которые существенно превышают ожидаемые при данных условиях.

Поскольку истинное значение измеряемой величины нам неизвестно, то на практике определяют интервал, в пределах которого заключено истинное значение измеряемой величины.

2. Расчет погрешности прямых измерений

2.1. Элементы математической статистики

Пусть проведено измерение (многократное наблюдение) некоторой физической величины а и в результате получен ряд ее значений:

.

Эти значения в большинстве своем отличаются друг от друга. Будем считать, что это отличие вызвано присутствием только случайных погрешностей, т.е. мы имеем результаты наблюдений случайной величины.

Случайной называется величина, которая может принять то или иное значение, причем заранее неизвестно, какое именно. Случайная величина оценивается вероятностью. Согласно определению, вероятностью Р какой-либо случайной величины а называется предел отношения числа случаев появления данной случайной величины n_i к общему числу всех проведенных опытов n при :

Вероятность принято выражать в долях единицы или в процентах. Из данного определения следует, что вероятность Р удовлетворяет неравенству .

Смысл понятия вероятности заключается в том, что на основании опыта более вероятными считают те события, которые происходят чаще, менее вероятными - те, что происходят реже.

В теории вероятности доказывается, что из всего ряда значений величины а наилучшим, т.е. наиболее близким к истинному является среднее арифметическое значение результатов наблюдений:

.

Тогда погрешности отдельных наблюдений определятся как

,

,

.......................

.

Как величины случайные, погрешности могут принимать разные значения с разной вероятностью. Описание совокупности значений случайной величины с указанием вероятности каждого значения называется законом распределения этой величины.

В практике измерений наибольшее распространение имеет нормальный закон распределения (закон Гаусса). В основе распределения Гаусса лежат два предположения:

1. при большом числе наблюдений погрешности равной величины, но разного знака встречаются одинаково часто, т.е. равновероятны;

2. вероятность появления погрешностей уменьшается с ростом величины погрешности, т.е. большие по абсолютной величине погрешности встречаются реже, чем малые. Наиболее вероятным является среднее арифметическое значение.

Кривая нормального распределения симметрична относительно среднего значения и описывается функцией Гаусса, аналитическое выражение которой имеет вид:

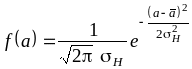
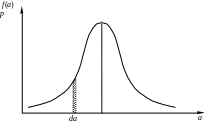
Рис. 1.

Функция распределения f(a) имеет смысл плотности вероятности: , где представляет вероятность появления отдельного случайного значения величины а в интервале значений от а до . Геометрически эта вероятность представляет собой площадь под кривой f(a), ограниченную отрезком da. Вся площадь под кривой (полная вероятность) равна

.

Параметр _Н характеризует степень рассеяния результатов наблюдений относительно среднего значения , т.е. определяет форму кривой распределения. С увеличением _Н максимальная ордината кривой Гаусса уменьшается. Поскольку площадь под кривой всегда одинакова и равна единице, то с увеличением _Н кривая растягивается вдоль оси абсцисс. Разброс значений относительно увеличивается, качество измерений ухудшается.

К ривая 2 нормального распределения, представленного на рисунке, соответствует большему, а кривая 1 - меньшему значению _Н, т.е. . Это означает, что в первом случае измерения проведены более качественно, чем во втором.

Значения соответствуют точкам перегиба функции f(a). Вероятность того, что случайная величина принимает значение, принадлежащее интервалу

Рис.2.

от до , равна 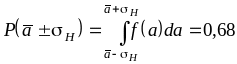или 68% (геометрически - это заштрихованная часть площади на графике). Вероятность того, что случайная величина принимает значение, принадлежащее интервалу от до , равна (95%), а для интервала от до вычисленная вероятность составляет или 99,7%.

Вероятность, с которой величина а заключена в интервале значений , называется доверительной вероятностью Р , а интервал носит название доверительного. Абсолютная случайная погрешность равна половине доверительного интервала.

Среднее арифметическое всегда отличается от истинного и лишь при совпадает с ним. Оно само является случайной величиной, подчиняется распределению Гаусса и характеризуется средним квадратичным отклонением результата измерения S, связанным с _Н выражением:

.

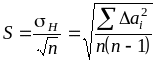При ограниченном числе наблюдений (2<n<30) коэффициент t зависит не только от доверительной вероятности P, но и от числа наблюдений n. Этот коэффициент, называется коэффициентом Стьюдента t_Pn, его значения приведены в таблице 1. Абсолютная случайная погрешность в этом случае рассчитывается по формуле

.

Таблица 1

P N	0,5	0,6	0,7	0,8	0,9	0,95	0,99
2	1,00	1,38	2,0	3,1	6,3	12,7	637
3	0,82	1,06	1,5	1,9	2,9	4,3	35
4	0,77	0,98	1,3	1,6	2,4	3,2	12,9
5	0,74	0,94	1,2	1,5	2,1	2,8	8,6
6	0,73	0,92	1,2	1,5	2,0	2,6	6,9
7	0,72	0,91	1,1	1,4	1,9	2,4	6,0
8	0,71	0,90	1,1	1,4	1,9	2,4	5,4
9	0,71	0,89	1,1	1,4	1,9	2,3	5,0
10	0,70	0,88	1,1	1,4	1,8	2,3	4,8