Критерий согласия Пирсона
Рассмотрим один из вопросов, связанных с проверкой правдоподобия гипотез, а именно – вопрос согласованности теоретического и статистического распределения.
Допустим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой (рис. 5.3). Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Естественно возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченный числом наблюдений, или они являются существенными и связаны с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат так называемые «критерии согласия».
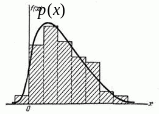
Рис. 5.3
Идея
применения критериев согласия заключается
в следующем. На основании данного
статистического материала нам предстоит
проверить гипотезу 
,
состоящую в том, что случайная величина 
подчиняется
некоторому определенному закону
распределения. Этот закон может быть
задан в той или иной форме: например, в
виде функции распределения 
или
в виде плотности распределения
или
же в виде совокупности вероятностей 
,
где
- вероятность того,
что величина
попадет
в пределы 
-го
разряда.
Для того чтобы
принять или опровергнуть гипотезу
,
рассмотрим некоторую величину 
,
характеризующую степень расхождения
теоретического и статистического
распределений. Величина
может
быть выбрана различными способами;
например, в качестве
можно
взять сумму квадратов отклонений
теоретических вероятностей
от
соответствующих частот 
или
же сумму тех же квадратов с некоторыми
коэффициентами («весами»), или же
максимальное отклонение статистической функции
распределения 
от
теоретической
и
т. д. Допустим, что величина
выбрана
тем или иным способом. Очевидно, это
есть некоторая случайная величина.
Закон распределений этой случайной
величины зависит от закона распределения
случайной величины
,
над которой производились
опыты, и от числа опытов 
.
Если гипотеза
верна,
то закон распределения величины
определяется
законом распределения величины
и числом
.
Рассмотрим один
из наиболее часто применяемых критериев
согласия - так называемый «критерий 
»
Пирсона.
Предположим, что
произведено
независимых
опытов, в каждом из
которых случайная величина
приняла
определенное значение. Результаты
опытов сведены в 
разрядов
и оформлены в виде статистического ряда:
|
|
|
………… |
|
|
|
|
…………. |
|
Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина имеет данный закон распределения (заданной функцией распределения или плотностью ). Назовем этот закон распределения «теоретическим».
Зная закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов:
.
Проверяя
согласованность теоретического и
статистического распределений, мы будем
исходить из расхождений между
теоретическими вероятностями
и
наблюденными частотами 
.
Схема применения критерия к оценке согласованности теоретического и статистического распределений сводится к следующему:
1) Определяется мера расхождения по формуле:
,
(5.5)
где 
-
число значений в
-м
разряде.
2)
Определяется число степеней свободы 
как
число разрядов
минус
число наложенных связей 
:
.
Примерами таких связей может быть:
1.
,
если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);
2.
,
если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое математическое ожидание и статистическое среднее значение;
3.
,
если мы требуем, кроме того, совпадения теоретической и статистической дисперсий и т.д.
3)
По
и
с
помощью табл. 1 определяется вероятность того,
что величина, имеющая распределение
с
степенями
свободы, превзойдет данное значение
.
4) Если эта вероятность меньше уровня значимости, гипотеза отбрасывается как неправдоподобная. Если эта вероятность больше или равна уровню значимости, гипотезу можно признать не противоречащей опытным данным.
Таблица 1.
Число степеней свободы
|
Вероятность P(χ2 > χα2) |
|||||||||
0.95 |
0.9 |
0.8 |
0.7 |
0.5 |
0.3 |
0.2 |
0.1 |
0.05 |
|
|
1 |
0.004 |
0.016 |
0.064 |
0.148 |
0.455 |
1.074 |
1.642 |
2.71 |
3.84 |
|
2 |
0.103 |
0.211 |
0.446 |
0.713 |
1.386 |
2.41 |
3.22 |
4.6 |
5.99 |
|
3 |
0.352 |
0.584 |
1.005 |
1.424 |
2.37 |
3.66 |
4.64 |
6.25 |
7.82 |
|
4 |
0.711 |
1.064 |
1.649 |
2.2 |
3.36 |
4.88 |
5.99 |
7.78 |
9.49 |
|
5 |
1.145 |
1.610 |
2.34 |
3 |
4.35 |
6.06 |
7.29 |
9.24 |
11.07 |
|
6 |
1.635 |
2.2 |
3.07 |
3.83 |
5.35 |
7.23 |
8.56 |
10.64 |
12.59 |
|
7 |
2.17 |
2.83 |
3.82 |
4.64 |
6.35 |
8.38 |
9.8 |
12.02 |
14.07 |
|
8 |
2.73 |
3.49 |
4.59 |
5.53 |
7.34 |
9.52 |
11.03 |
13.36 |
15.51 |
|
9 |
3.32 |
4.17 |
5.38 |
6.39 |
8.34 |
10.66 |
12.24 |
14.68 |
16.92 |
|
10 |
3.94 |
4.86 |
6.18 |
7.27 |
9.34 |
11.78 |
13.44 |
15.99 |
18.31 |
|
11 |
4.58 |
5.58 |
6.99 |
8.15 |
10.34 |
12.9 |
14.63 |
17.28 |
19.68 |
|
12 |
5.23 |
6.3 |
7.81 |
9.03 |
11.34 |
14.01 |
15.81 |
18.55 |
21 |
|
13 |
5.89 |
7.04 |
8.63 |
9.93 |
12.34 |
15.12 |
16.98 |
19.81 |
22.4 |
|
14 |
6.57 |
7.79 |
9.47 |
10.82 |
13.34 |
16.22 |
18.15 |
21.1 |
23.7 |
|
15 |
7.26 |
8.55 |
10.31 |
11.72 |
14.34 |
17.32 |
19.31 |
22.3 |
25 |
|
16 |
7.96 |
9.31 |
11.15 |
12.62 |
15.34 |
18.42 |
20.5 |
23.5 |
26.3 |
|
17 |
8.67 |
10.08 |
12.00 |
13.53 |
16.34 |
19.51 |
21.6 |
24.8 |
27.6 |
|
18 |
9.39 |
10.86 |
12.86 |
14.44 |
17.34 |
20.6 |
22.8 |
26 |
28.9 |
|
19 |
10.11 |
11.65 |
13.72 |
15.35 |
18.34 |
21.7 |
23.9 |
27.2 |
30.1 |
|
20 |
10.85 |
12.44 |
14.58 |
16.27 |
19.34 |
22.8 |
25 |
28.4 |
31.4 |
|
Л.5.4 Методические указания к выполнению работы
Необходимо получить вариант задания у преподавателя.
Таблица Л.5.1 – Варианты задания для выполнения лабораторной работы
Параметры сети |
Номер варианта |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Номер иссл-го кластера, nn |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
Количество РЭС каждого кластера сети, mn
|
[51 31 41]
|
[21 31 21] |
[21 31 41]
|
[32 22 42]
|
[21 41 31]
|
[21 21 22]
|
[25 21 21]
|
[21 36 25]
|
[21 31 36]
|
[34 31 31]
|
Закон распределения РЭС в пространстве, i3 |
нормальное |
нормальное |
нормальное |
равномерное |
равномерное |
равномерное |
нормальное |
нормальное |
нормальное |
равномерное |
Уровень значимости, lam |
0.05 0.1 |
0.1 0.2 |
0.2 0.3 |
0.3 0.05
|
0.05 0.1 |
0.1 0.2 |
0.2 0.3 |
0.3 0.05
|
0.05 0.1 |
0.1 0.2 |
Координаты вновь введенного РЭС, p |
[8;6;0.6]
|
[10;3;0.4] |
[10;14;8] |
[1;8;6]
|
[7;1;0.6] |
[14;14;7] |
[2;10;7]
|
[6;4;0.7] |
[10;10;10] |
[3;10;4] |
Задание.
2.1. Открыть программу Lb_5_2.m. Для ее работы необходимо наличие подпрограмм korran1.m razm.m, и razm1.m. Ввести данные согласно полученному варианту.
2.2. Показать размещение РЭС всех кластеров в пространстве.
2.3. Показать размещение РЭС всех кластеров на плоскости.
2.4. Определить математические ожидания и дисперсии координат РЭС, исследуемой сети по оси х, оси y и оси z
2.5. Построить гистограмму плотности распределения координат размещения РЭС по оси х. Построить гистограмму плотности распределения координат размещения РЭС по оси y. Построить гистограмму плотности распределения координат размещения РЭС по оси z. На этих же графиках построить теоретическую плотность распределения вероятностей. Выдвинуть гипотезу о нормальном распределении. Рассчитать χ2 и определить вероятность P(χ2 > χα2). Для заданного уровня значимости получить подтверждение или отвергнуть гипотезу с помощью критерия согласия Пирсона.
2.6. Рассчитать расстояния между РЭС, исследуемого кластера. В отчете отобразить расстояния между РЭС от 1 до 6.
2.7. С помощью нейронной сети Кохонена определить центры кластеров и показать их уже сформированных кластерах в пространстве и на плоскости. Здесь же показать вновь введеное РЭС.
2.8. С помощью нейронной сети Кохонена определить к какому из кластеров относится вновь введенное РЭС.
2.9. Изменить уровень значимости. Построить гистограмму плотности распределения координат размещения РЭС по оси х. Построить гистограмму плотности распределения координат размещения РЭС по оси y. Построить гистограмму плотности распределения координат размещения РЭС по оси z. На этих же графиках построить теоретическую плотность распределения вероятностей. Выдвинуть гипотезу о нормальном распределении. Рассчитать χ2 и определить вероятность P(χ2 > χα2). Для заданного уровня значимости получить подтверждение или отвергнуть гипотезу с помощью критерия согласия Пирсона.
Сделать выводы по работе.
Л.5.5 Контрольные вопросы
1. Что такое сенсорная сеть?
2. Области применения сенсорных сетей.
3. Что такое кластерный анализ?
4. Что из себя представляет нейронная сеть Кохонена?
5. Что такое критерий согласия Пирсона? Его назначение.
Литература к лабораторной работе №5
1. Терентьев М. Н. Модель беспроводной сенсорной сети с режимом сбережения энергии и синхронизацией шкал времени [Текст] / Вестник Московского авиационного института.– Москва: МАИ, 2009. – Т. 16. – № 4. C. 79–84
2. Иванова, И. А. Определение периметра зоны покрытия беспроводных сенсорных сетей [Текст] / И. А. Иванова // Промышленные АСУ и контроллеры. – 2010. – № 10. – С. 25–30.
3. G.D. Abowd, J.P.G. Sterbenz, Final report on the interagency workshop on research issues for smart environments, IEEE Personal Communications (October 2000) 36–40.
4. Круг П.Г. Нейронные сети и нейрокомпьютеры: Учебное пособие по курсу
«Микропроцессоры». – М.: Издательство МЭИ, 2002. – 176 с. ISBN 5-7046-0832-9