Последовательное соединение r, l, c в цепи переменного тока. Закон Ома
При последовательном соединении токи, протекающие по всем элементам цепи, одинаковы, а мгновенные значения напряжений складываются, то есть
.
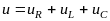Таким образом, в результате сложения трех колебаний получается четвертое.
Для сложения колебаний применим метод векторных диаграмм. Вы разим амплитудные значения напряжений на участках цепи через амплитудные значения силы тока:
,
, 
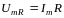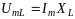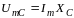. (1)
Выделим
направление и обозначим его как ось
токов.
Поскольку сдвиг фаз между током и
напряжением на активном сопротивлении
равен нулю, вектор напряжения длиной,
равной амплитуде
,
направим по оси токов. Учитывая, что на
индуктивном сопротивлении напряжение
опережает ток на
,
вектор
направим перпендикулярно оси токов
вверх (будем считать положительными
углы поворота против часовой стрелки).
Тогда вектор, изображающий напряжение
на емкости
,
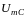которое отстает от тока на
,
будет ориентирован противоположно
вектору
.
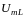Результатом сложения этих трех векторов
будет вектор длиной
.
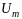В
начале
сложим противоположно направленные
векторы
и
.
Затем применим теорему Пифагора, согласно
которой
.
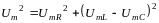Подставим в эту формулу выражения (1)
,
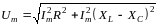откуда выразим амплитуду силы тока
.
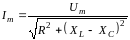Эту формулу можно записать в виде
,
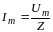она представляет закон Ома для участка цепи, содержащего последовательно соединенные активное, емкостное и индуктивное сопротивления. Величину
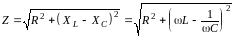
называют полным сопротивлением цепи переменного тока или импедансом.
С помощью векторной диаграммы найдем сдвиг фаз между током и напряжением:
.
В
практике широко применяют так называемый
коэффициент
мощности,
равный
.
Из векторной диаграммы видно, что
.
Применяя закон Ома, получаем, что
,
или
.
В
рассматриваемой цепи ток
будет максимальным,
если
,
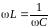то есть напряжения на индуктивном и
емкостном сопротивлениях совпадают по
величине:
.
Это явление называется резонансом
напряжений.
При резонансе полное сопротивление цепи минимально и равно активному сопротивлению: Z = R, сдвиг фаз между током и напряжением равен нулю.
Параллельное соединение r, l, c в цепи переменного тока
П
ри
параллельном соединении напряжения на
всех элементах цепи, одинаковы и равны
внешнему напряжению, а мгновенные
значения токов складываются, то есть
.
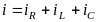Таким образом, в результате сложения трех колебаний получается четвертое.
Также, как и раньше, для сложения колебаний применим метод векторных диаграмм. По закону Ома для участков цепи имеем
,
, 
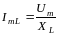. (1)
Выделим
направление и обозначим его как ось
напряжений.
Поскольку сдвиг фаз между током и
напряжением на активном сопротивлении
равен нулю, вектор тока длиной, равной
амплитуде
,
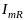направим по оси напряжений. Учитывая,
что на индуктивном сопротивлении
напряжение опережает ток на
,
вектор
направим перпендикулярно оси токов
вниз. Тогда вектор, изображающий ток на
электроемкости
,
который опережает напряжение на
,
будет ориентирован противоположно
вектору
.
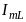Результатом сложения этих трех векторов
будет вектор длиной
.
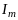В
начале
сложим противоположно направленные
векторы
и
.
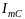Затем применим теорему Пифагора, согласно
которой
.
Подставим в эту формулу выражения (1)
,
откуда выразим амплитуду напряжения
.
Эту формулу можно записать в виде
,
она представляет закон Ома для участка цепи, содержащего параллельно соединенные активное, емкостное и индуктивное сопротивления. Величину
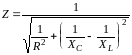
называют полным сопротивлением цепи переменного тока или импедансом.
Из
векторной диаграммы видно, что при
выполнении условия
,
или, что то же самое,
полное сопротивление цепи минимально
и равно активному сопротивлению: Z
= R.
Токи на индуктивном и емкостном
сопротивлениях совпадают по величине:
,
сдвиг фаз между током и напряжением
равен нулю. Это явление называется
резонансом
токов