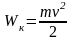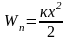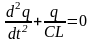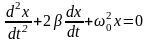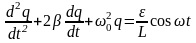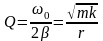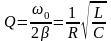- •Колебания и волны
- •Переменный ток
- •Контур с активным сопротивлением
- •Контур с электроемкостью
- •Контур с индуктивностью
- •Последовательное соединение r, l, c в цепи переменного тока. Закон Ома
- •Параллельное соединение r, l, c в цепи переменного тока
- •Комбинированное соединение r, l, c в цепи переменного тока
- •Мощность, выделяемая в цепи переменного тока
- •Примеры решения задач.
Колебания и волны
Колебательным движением или колебанием называются движения или процессы, которые характеризуются повторяемостью во времени тех или иных значений физических величин.
Колебательные процессы широко распространены в природе и технике и представляют собой сложные процессы. Физическая природа может быть разной, поэтому различаются: механические, электромагнитные и т.д., но различные колебательные процессы описываются одинаковыми характеристиками и однотипными уравнениями.
МЕХАНИЧЕСКИЕ |
ЭЛЕКТРОМАГНИТНЫЕ |
|
Масса m |
Индуктивность L |
|
Жесткость k |
Величина, обратная электроемкости 1/C |
|
Смещение (координата) x |
Заряд конденсатора q(t) |
|
Скорость v = dx/dt |
Ток в цепи I = dq/dt |
|
Ускорение a = d2x/dt2 |
Скорость изменения тока d2q/dt2 |
|
Импульс Р = m v |
Магнитный поток Ф = LI |
|
Сила (упругая F = kx) F |
Напряжение U = q/C |
|
Частота свободных колебаний
|
|
|
Период
|
|
|
Кинетическая энергия
|
Магнитная
энергия катушки
|
|
Потенциальная
энергия деформации (пружина)
|
Энергия электрического поля (конденсатора)
|
|
Дифференциальные уравнения гармонических колебаний |
||
|
|
|
|
|
|
решением этих уравнений являются выражения: |
||
х
= А sin
(ω0t
+ φ0) |
q = q0 sin (ω0t + φ0) |
|
Уравнения затухающих колебаний: |
||
|
|
|
решением этих уравнений являются выражения: |
||
x(t) = x0e-βt cos (ωt + φ0) |
q(t) = q0 e-βt cos (ωt + φ0) |
|
Коэффициент затухания β = r/2m |
β = R/2L |
|
Коэффициент сопротивления r |
R |
|
Уравнения вынужденных колебаний: |
||
|
|
|
х = А sin (ωt - φ0) |
q = q0 сos (ωt - φ0) |
|
Добротность пружинного маятника
|
Добротность колебательного контура
|
|
Для возбуждения и поддерживания электромагнитных колебаний используется колебательный контур – это цепь, состоящая из последовательно соединенных: катушки, конденсатора и сопротивления.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
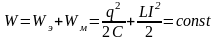
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис.1).
|
Рисунок 1. Затухающие колебания в контуре.
Таким образом, затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Затухание механических колебаний вызывается трением; в электрических колебательных системах – тепловыми потерями на активном сопротивлении R, а также потерями в диэлектриках и ферромагнетиках, вследствие гистерезиса.
Отношение амплитуд двух последующих затуханий называется декрементом затухания, а логарифм – логарифмическим декрементом затухания:

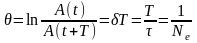
Ne – число колебаний, совершаемых за время уменьшения амплитуды в е раз.
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – rυ. Коэффициент r в этой формуле аналогичен сопротивлению R в электрическом контуре. сопротивления R контура. Интервал времени, в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
Колебания, возникающие под действием внешней периодически изменяющейся силы или э.д.с., называются вынужденными колебаниями.
Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающих колебаний 0 к частоте, равной или близкой к собственной частоте колебательной системы, называется резонансом. Резонансная частота равна

Где = R/2L. При 2 02 значение рез практически совпадает с собственной частотой колебательной системы.
Добротность характеризует резонансные свойства колебательной системы, чем больше Q, тем больше Арез. (Чем меньше затухание, тем больше добротность Q).
Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
|
|
|
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.



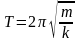
 -
формула
Томпсона
-
формула
Томпсона