Техника безопастности

1. К проведению работ допускаются лица, прошедшие инструктаж по технике безопасности.

2. При выполнении работы необходимо соблюдать меры предосторожности при работе с физическим маятником и математическим маятниками.

4. Порядок выполнения работы

Используя математический и физический маятники, необходимо определить ускорение свободного падения для данной местности.

ЗАДАНИЕ 1. Измерить ускорение свободного падения при помощи математического маятника.

Описание установки

Из формулы (16) получим:

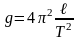. (21)

Из определения периода колебаний:

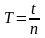, (22)

где t – время, за которое совершается n колебаний.

1). Задавшись определенным значением точности расчета g -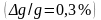 , вычислить количество колебаний n, которое необходимо провести для получения результата с заданной точностью.

Измерение g является косвенным измерением. Для получения формулы для расчета ошибки косвенного измерения надо проделать следующие преобразования формулы (19):

1) прологарифмировать формулу по основанию натурального логарифма:

;

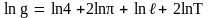2) полученную формулу продифференцировать:

;

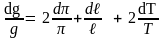3) перейти к конечным изменениям величин, входящих в формулу:

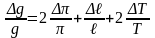. (23)

Обычно погрешность 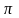в лабораторных измерениях берется 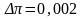. Ошибка измерения длины математического маятника 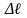равна точности измерения применяемого для этого прибора.

Из формулы (23) следует, что точность измерения ускорения свободного падения зависит от точности измерения периода колебаний математического маятника .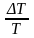

Тогда из формулы (23)следует

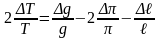. (24)

Из определения периода колебаний (22) и предположения, что Т также является косвенным измерением, получим:

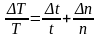. (25)

Пренебрегая 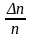и с учетом (24) и (25), получим:

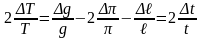, (26)

где 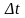– ошибка секундомера, равная цене деления секундомера. Из формулы (26) можно рассчитать время t, необходимое для получения заданной точности измерения ускорения свободного падения g. Однако, при проведении экспе

римента, лучше измерять не время колебаний t, а число колебаний n, происходящих за это время. Для нахождения n используют формулу (22), в которую вместо Т подставляют предварительно найденный период колебаний маятника Т_пр и рассчитанное из формулы (26) время t.

Необходимо, однако, привести некоторые соображения по поводу оценки погрешности и точности определения величины ускорения свободного падения с помощью данного маятника.

Считая, что период колебаний маятника определяется формулой (22), мы пренебрегаем зависимостью периода от амплитуды и неизбежным нарушением требований, вытекающих из определения математического маятника. Это влечет за собой следующие неточности:

I. Строго говоря, период колебаний зависит от амплитуды колебаний:

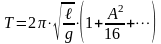. (27)

Такое выражение для периода колебаний следует из решения уравнения (16).

В нашей работе мы пренебрегаем членами, содержащими амплитуду колебаний, следствием чего является погрешность 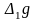в определении g. Из формулы (23) найдем ускорение свободного падения:

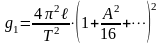. (28)

Погрешность найдем как разность между более точным значением, которое дается формулой (26) и приближенным, которое дается формулой (19):

;

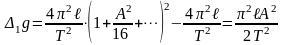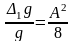, (29)

где А выражено в радианах.

II. Конечность размеров шарика, наличие в нем отверстия, весомость нити и наличие узелка на ее конце приводят к тому, что данный маятник не является строго математическим, поэтому для расчета ускорения свободного падения нужно пользоваться формулой (18), а не формулой (15). Использование формулы (19) для расчета g без учета отличия параметров нашего маятника от идеального математического маятника приводит к появлению погрешности 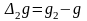. Значение 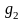рассчитывается из формулы (20), а 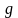– из формулы (16):

.

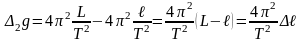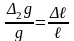. (30)

III. В результате растяжимости нити допускается погрешность

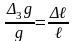, (31)

где – удлинение нити, вызванное действием максимальной центробежной силы в момент прохождения положения равновесия.

Однако в нашей установке погрешности (29), (30), (31) невелики. Например, 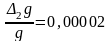для = 100 см, то есть на порядок меньше погрешностей величин, входящих в формулу (22). При малых колебаниях 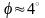величин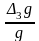а еще меньше. Поэтому погрешностям (29), (30), (31) можно пренебречь, если амплитуда

колебаний будет порядка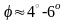 .