МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Электротехнический факультет

Кафедра физики

З.Г. Морозова

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО

ПАДЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО

И ФИЗИЧЕСКОГО МАЯТНИКОВ

Учебно-методическое пособие

к лабораторной работе по дисциплине «Физика»

Киров 2015

УДК 513(07)

О 62

Рекомендовано к изданию методическим советом электротехнического факультета ФГБОУ ВПО «ВятГУ»

Рецензент:

кандидат педагогических наук, доцент, кафедры «Прикладной математики и информатики» ФГБОУ ВПО «ВятГУ» Хохлова М. В.

Морозова З.Г.

Определение ускорения свободного падения с помощью математического и физического маятников: учебно-методическое пособие к лабораторной работе по дисциплине «Физика» для студентов всех технических профилей подготовки, всех форм обучения / З.Г. Морозова. – Киров: Изд–во ВятГУ, 2015. –19с.

© Морозова З.Г., 2015

© ФГБОУ ВПО «ВятГУ», 2015

Цель работы: изучение свойств гармонических колебаний на примере движения математического и физического маятников.

1. Гармонические колебания и их характеристики

Периодически повторяющиеся процессы или движения называются колебаниями. Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии и отсутствия внешних воздействий на колебательную систему в дальнейшем.

Простейшим типом свободных колебаний являются гармонические колебания. При гармонических колебаниях, независимо от природы возбуждения, изменение характерной величины S, происходит по закону косинуса или синуса:

S = A sin ,

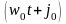S = A cos , (1)

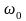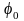где А – амплитуда колебаний – максимальное значение величины S; – круговая (циклическая) частота; – фаза колебаний; – начальная фаза колебаний.

Амплитуда колебаний А является энергетической характеристикой процесса. Полная энергия колебательной системы пропорциональна квадрату амплитуды. Амплитуда гармонических колебаний не меняется со временем, т. е. и полная энергия колебательной системы в процессе гармонических колебаний меняться не будет.

Циклическая частота 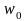зависит от периода колебаний Т – 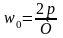. Период Т определяется конструктивными особенностями устройства колебательной системы.

Фаза колебаний –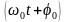 определяет смещение колеблющейся вели-

чины S(t) относительно положения равновесия в любой произвольный момент времени t.

Начальная фаза колебаний 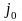– величина, определяющая смещение колеблющейся величины относительно положения равновесия в начальный момент времени S = S(t₀=0)= S₀ = A sin .

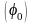Колебательные системы, совершающие механическое движение, называются маятниками. Для них величина S определяет X координату смещения маятника относительно положения равновесия.

Т.е уравнения (1) перепишутся:

X= X _m cos или

X= X _m sin , (2)

где X _m – максимальное смещение от положения равновесия – амплитуда колебания.

Зависимость координаты от времени X(t) – формулы (2) можно рассматривать как уравнения движения маятника.

Если уравнение движения маятника X= X _m cos ; тогда по определению мгновенная скорость и мгновенное ускорение маятника запишутся:

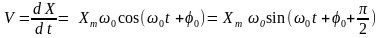(3)

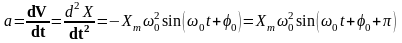(4)

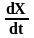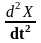Из сравнения уравнений (3) и (4) с уравнением X(t) (2) следует, что и скоростьV(t) и ускорение a(t), подобно координате X(t), со временем изменяются по гармоническому закону, но имеют смещения по фазе относительно X. Скорость опережает X по фазе на p/2(в те моменты времени, когда X (t) = 0, скорость V(t)=V_m -приобретает максимальное значение). Ускорение опережает X по фазе на p (в те моменты времени, когда

X (t) = X_m – принимает максимальное положительное значение , ускорение

a (t)= - a _m приобретает максимальное отрицательное значение ).

Из уравнения (3) амплитудное (максимальное) значение скорости равно 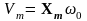, из уравнения (4) – амплитудное значение ускорения .

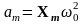Из сравнения уравнений для координаты – (2) и для ускорения – (4) следует:

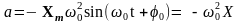(5)

Сила, действующая на колебательную систему, определяется по второму

закону Ньютона с учетом (5) выражением:

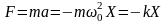, (6)

где m- масса колебательной системы, k= m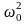 -постоянный для этой системы коэффициент.

Данная сила F подобна силе упругости, пропорциональна смещению X и направлена в противоположную сторону смещению. В общем случае эта сила F называется квазиупругой силой, а коэффициент k- коэффициентом квазиупругой силы.

Из уравнения (6) после определенных математических преобразований следует:

,

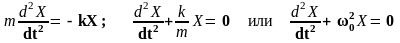где =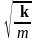 собственная частота колебаний маятника).

Полученное дифференциальное уравнение (8) называется дифференциальным уравнением механических гармонических колебаний:

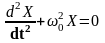(8)

Решением этого дифференциального уравнения являются функции вида (2).

В общем виде при X=S уравнение (8) принимает вид 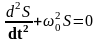(9)

(9)

Решением уравнения (9), является функции вида (1), а будет собственной частотой соответствующей колебательной системы.

Для гармонических механических колебаний характерно постоянство величины полной механической энергии системы (отсутствие затухания) и переход энергии в процессе движения из одного вида в другой и обратно без потерь

Для случая механического движения кинетическая энергия K определяется выражением:

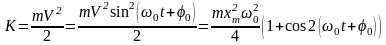. (10)

Потенциальная энергия П по определению с учетом (7) запишется:

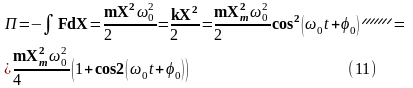
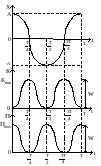
Рис.1

Полная энергия механическая энергия W равна сумме кинетической и потенциальной энергии и с учетом уравнений (10) и (11) определяется выражением и не меняется в процессе колебаний:

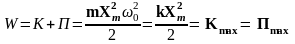. (12)

На рис. 1 представлены зависимости координаты X(t), кинетической энергии К(t), потенциально энергии П(t) и полной энергии W(t) от времени. гии П(t) и полной энергии W(t) от времени.

Из формул (10) и (11) и рис.1 следует, что и кинетическая и потенциальная энергия маятника изменяются с частотой, в два раза превышающей частоту соответствующего гармонического колебания X(t).

Кинетическая и потенциальная энергия имеют сдвиг по фазе на p, т.е. в момент, когда кинетическая энергия достигает максимума потенциальная энергия имеет минимум.