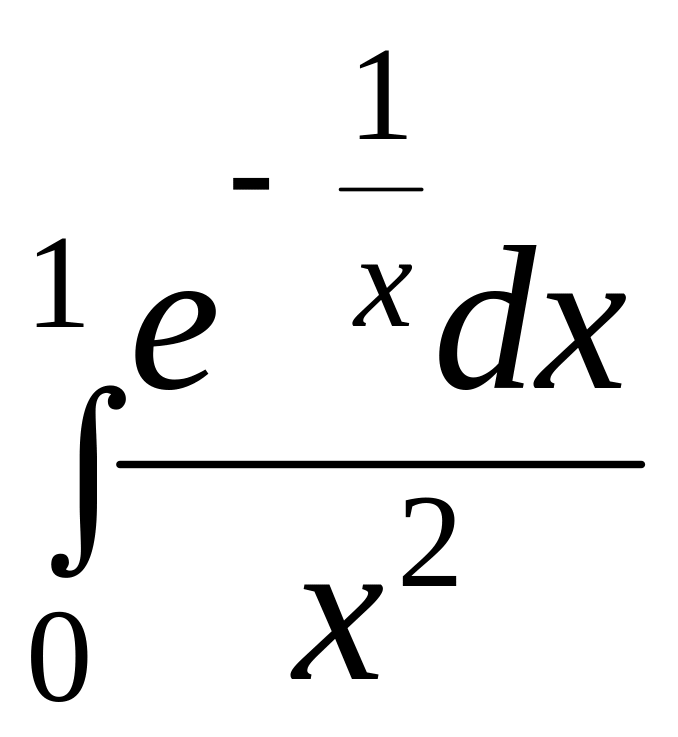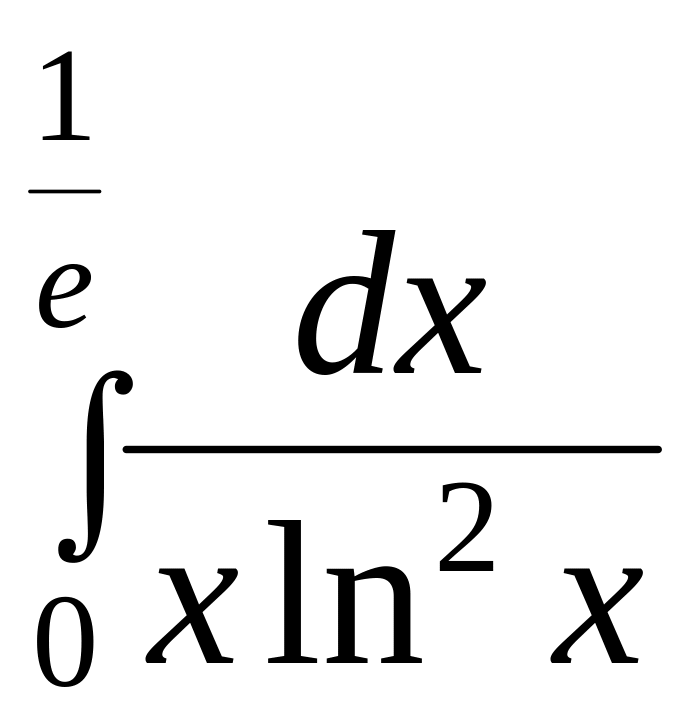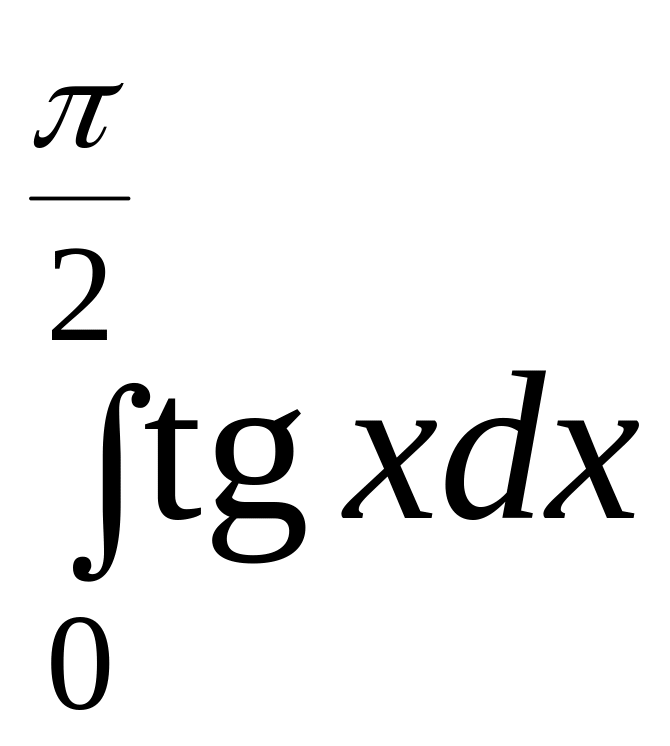- •Исходные данные для решения задачи
- •Задание № 2.
- •Исходные данные для решения задачи
- •Задание № 3.
- •Исходные данные для решения задачи
- •Задание № 4.
- •Исходные данные для решения задачи
- •Задание № 5.
- •Исходные данные для решения задачи
- •Задание № 6.
- •Исходные данные для решения задачи
- •Защита ргр № 2 «Определенный интеграл и его применение»
Задание № 6.
Вычислить несобственные интегралы или установить их расходимость.
Исходные данные для решения задачи
Номер варианта |
Интеграл |
Интеграл |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Критерии оценки:
Количество заданий: 6.
1 задание: 2 балла.
Максимальное количество баллов за письменную часть: 12 баллов.
Защита ргр № 2 «Определенный интеграл и его применение»
Теоретические вопросы:
Определение определенного интеграла
Свойства определенного интеграла;
Вывод формулы Ньютона-Лейбница;
Геометрический смысл определенного интеграла;
Формула интегрирования по частям в определенном интеграле;
Вычисление площади плоской фигуры с помощью определенного интеграла;
Вычисление длины дуги кривой с помощью определенного интеграла;
Вычисление объема тела вращения с помощью определенного интеграла;
Несобственные интегралы.
Задачи:
№ 1. Вычислить определенные интегралы:
1)
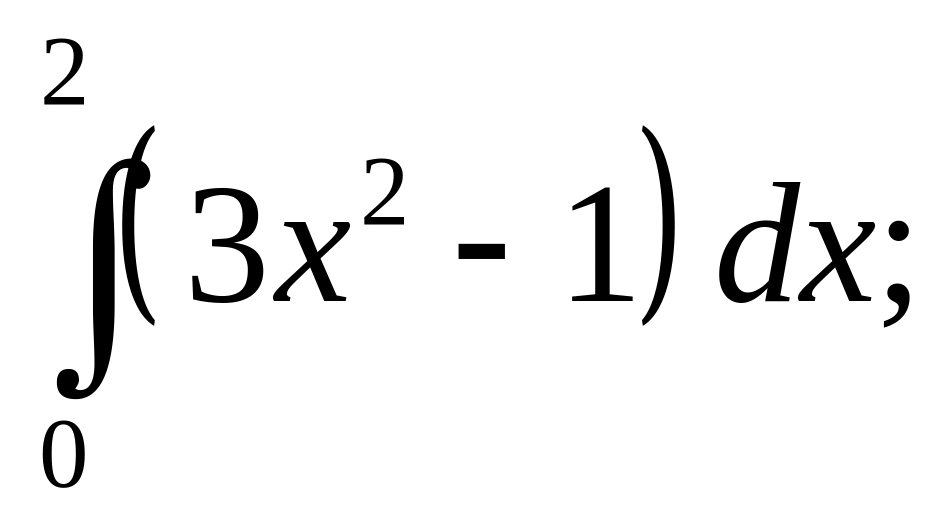
2)
![]()
3)
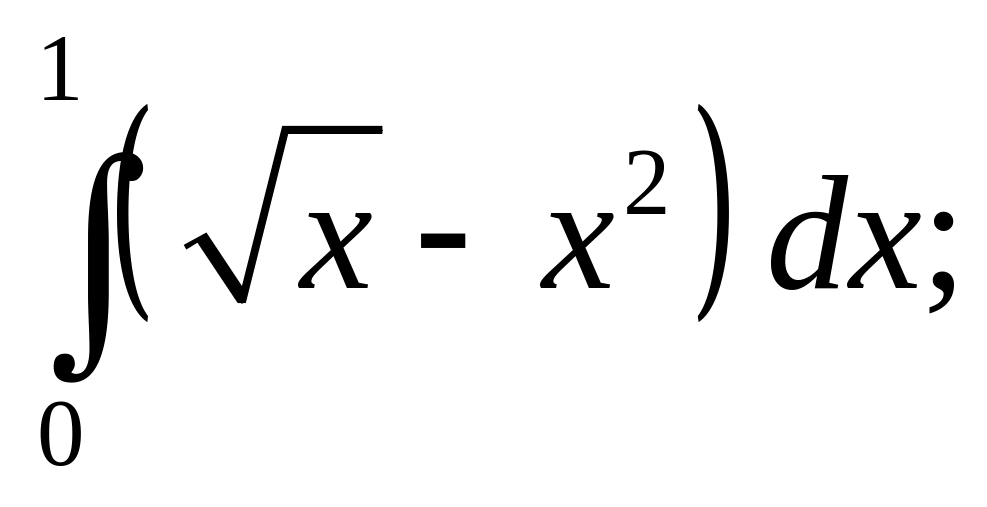
4)

5)
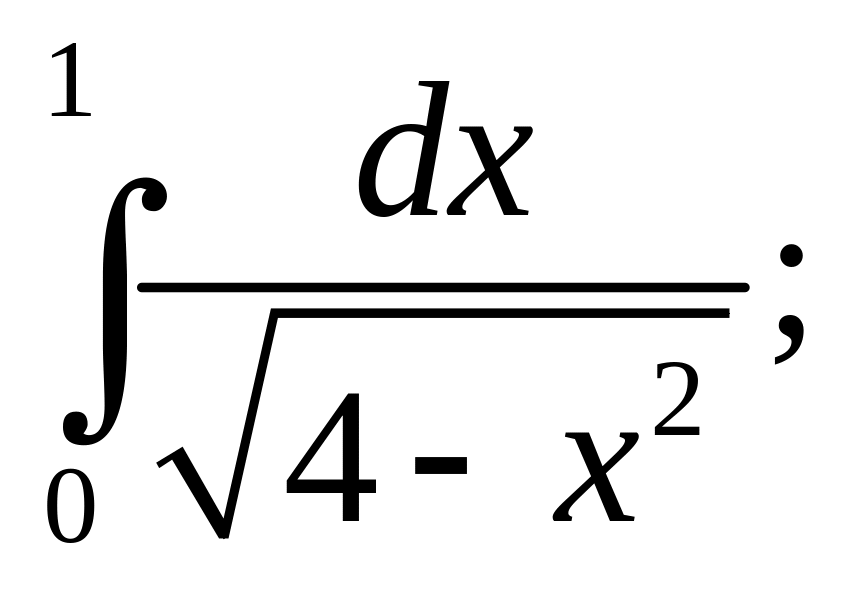
6)

7)
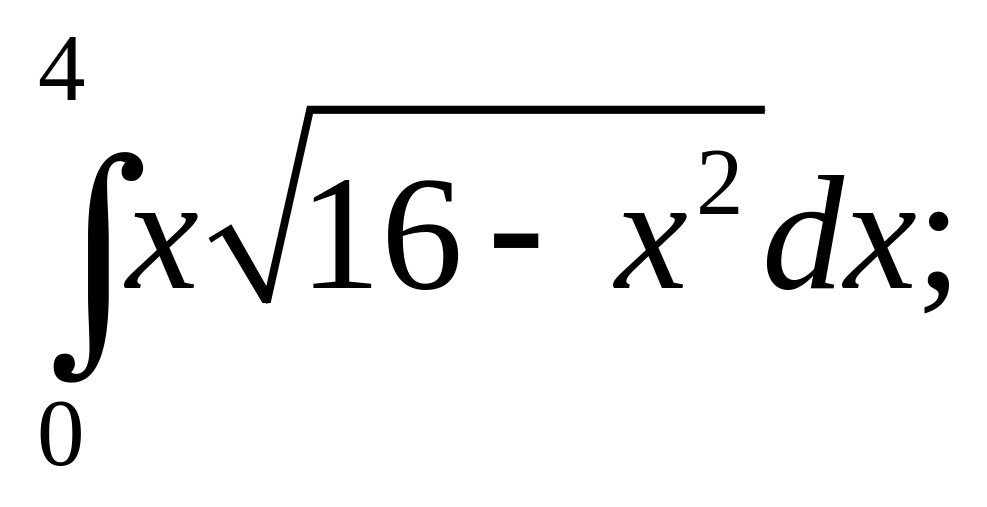
8)
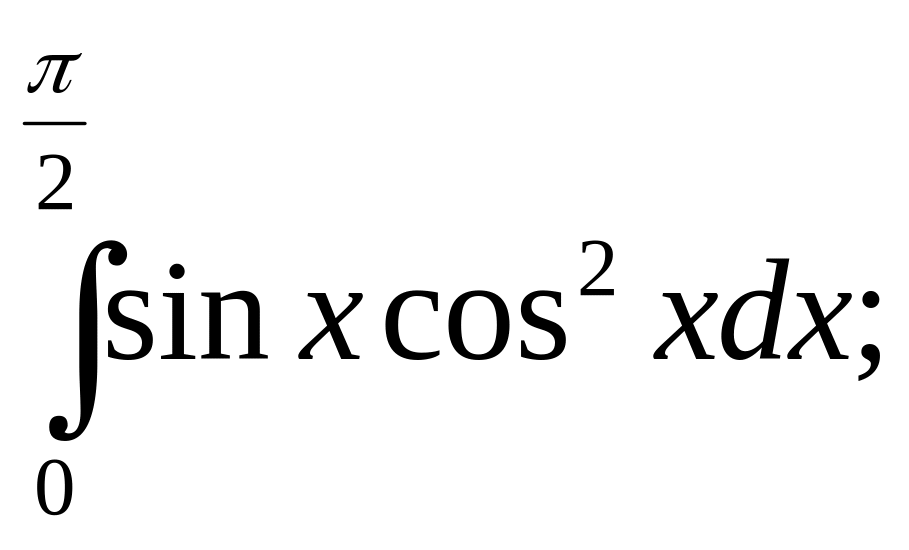
9)
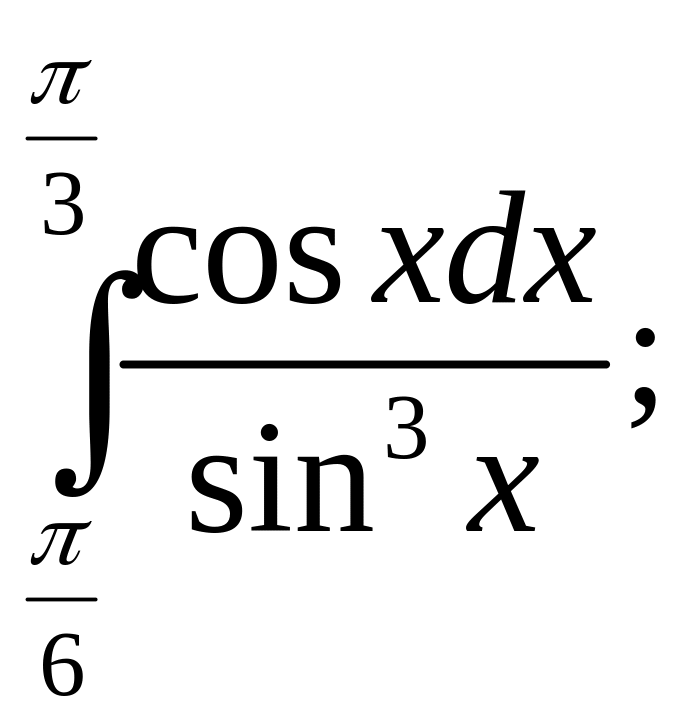
10)
![]()
11)
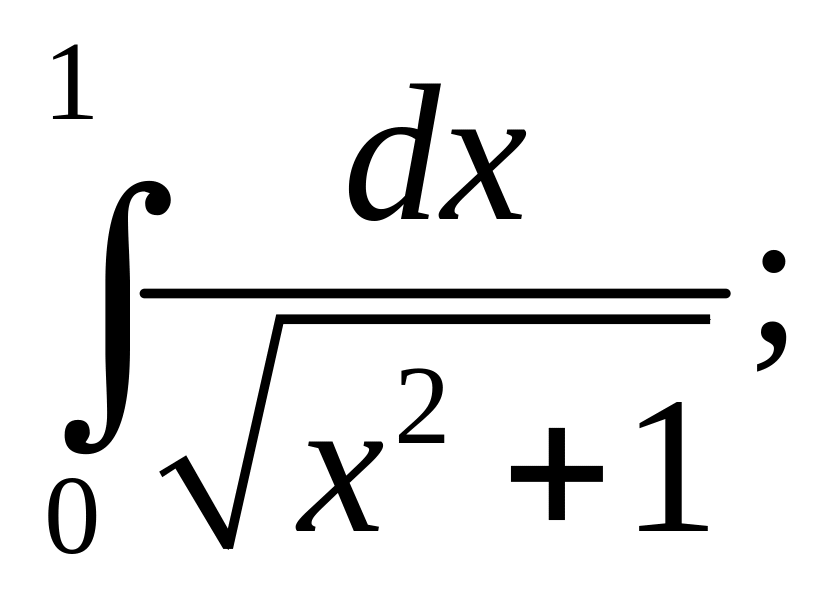
12)
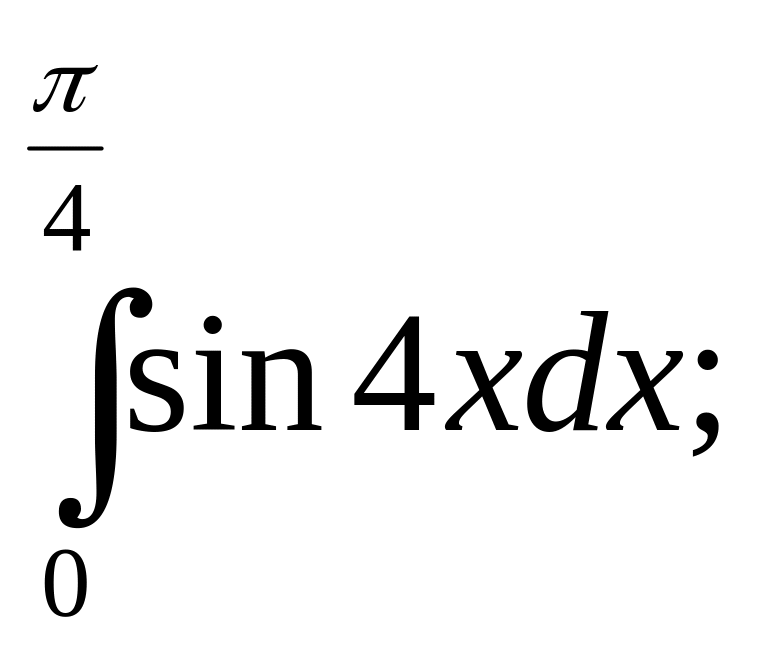
13)
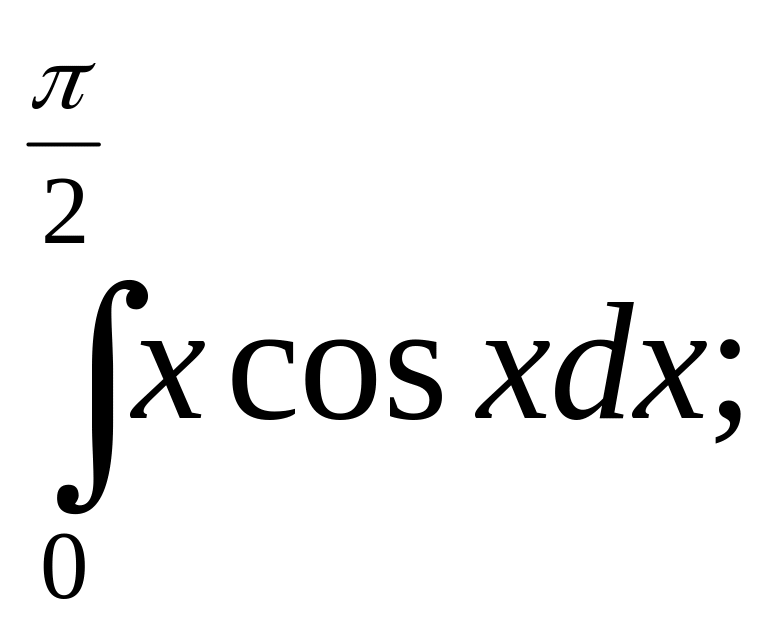
14)
![]() .
.
№ 2. Вычислить площадь фигуры, ограниченной линиями:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]() ;
;
7)
![]() и
и
![]() ;
;
8)
![]() и
и
![]() .
.
Изобразить фигуру.
№ 3. Вычислить площадь фигуры, ограниченной линией, заданной в полярной системе координат:
1)
![]() ;
;
2)
![]() ,
,
![]()
Изобразить фигуру.
№ 4. Вычислить длину дуги кривой:
1)
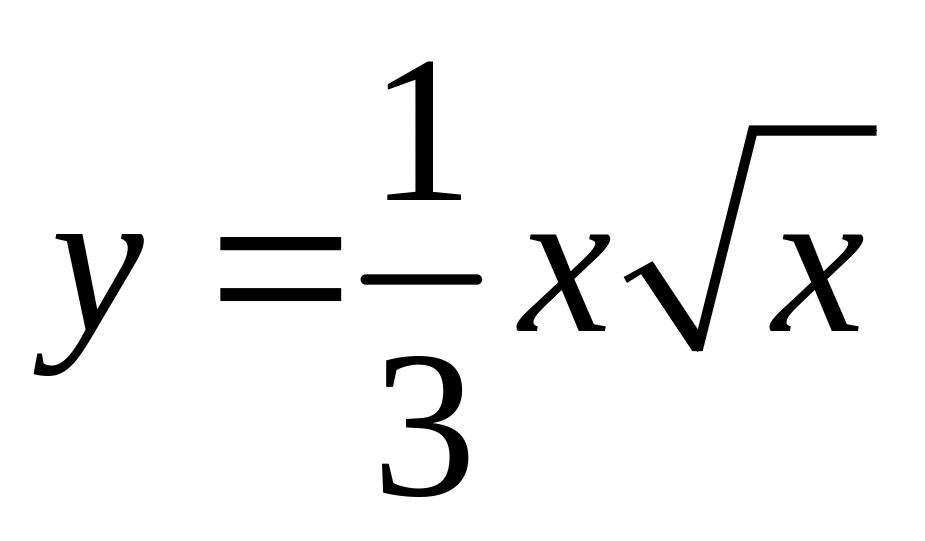 от
от
![]() до
до
![]() ;
;
2)
![]() от
от
![]() до
до
![]() .
.
№ 5. Вычислить длину дуги кривой, заданной параметрически:
1)
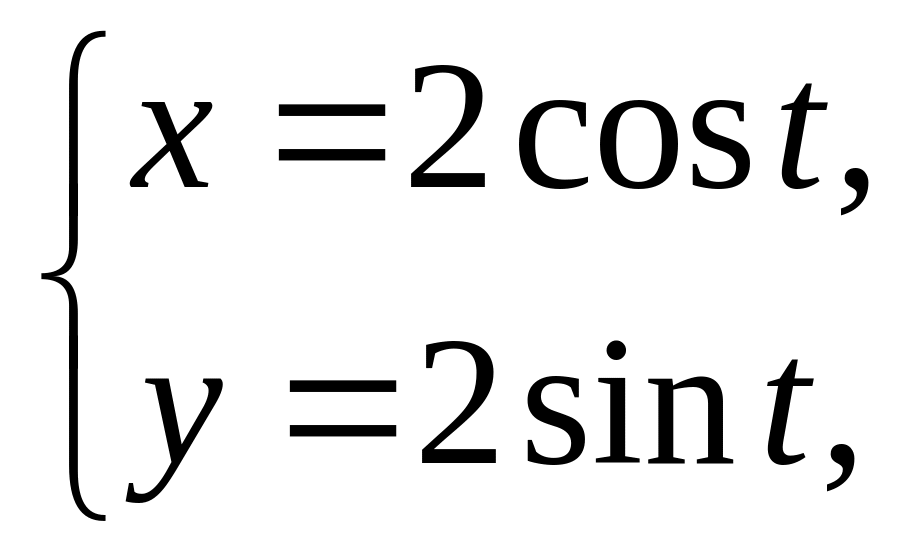 где
где
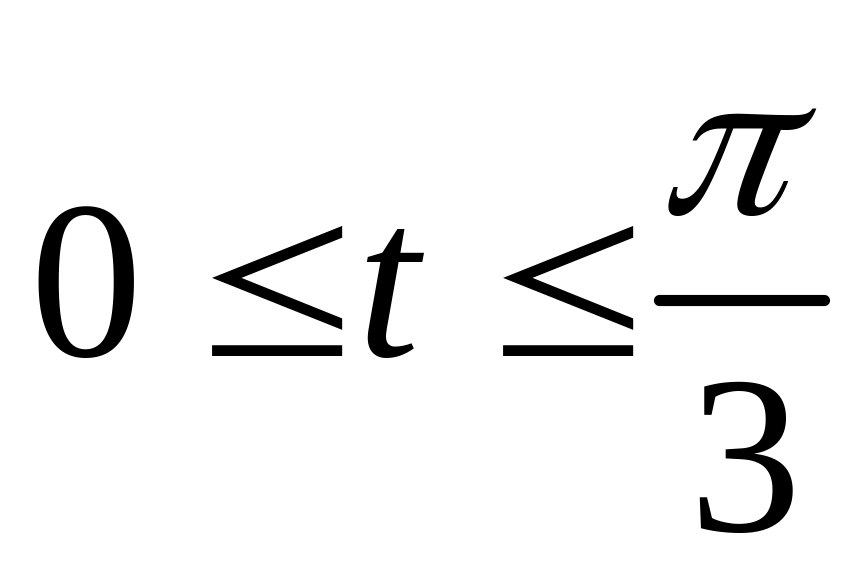 ;
;
2)
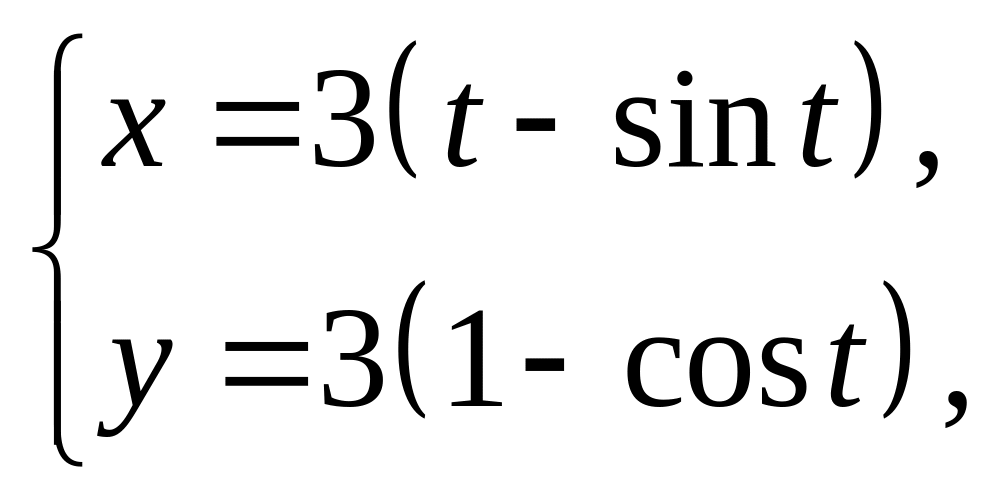 где
где
![]() .
.
№ 6. Вычислить длину дуги кривой, заданной в полярной системе координат:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() .
.
№ 7.
Вычислить объем тела, полученного
вращением вокруг оси
![]() фигуры,
расположенной в I четверти и ограниченной
параболой
фигуры,
расположенной в I четверти и ограниченной
параболой
![]() ,
прямой
,
прямой
![]() и осью
.
Сделать рисунок.
и осью
.
Сделать рисунок.
№ 8.
Вычислить объем тела, полученного
вращением вокруг оси
![]() фигуры,
ограниченной гиперболой
фигуры,
ограниченной гиперболой
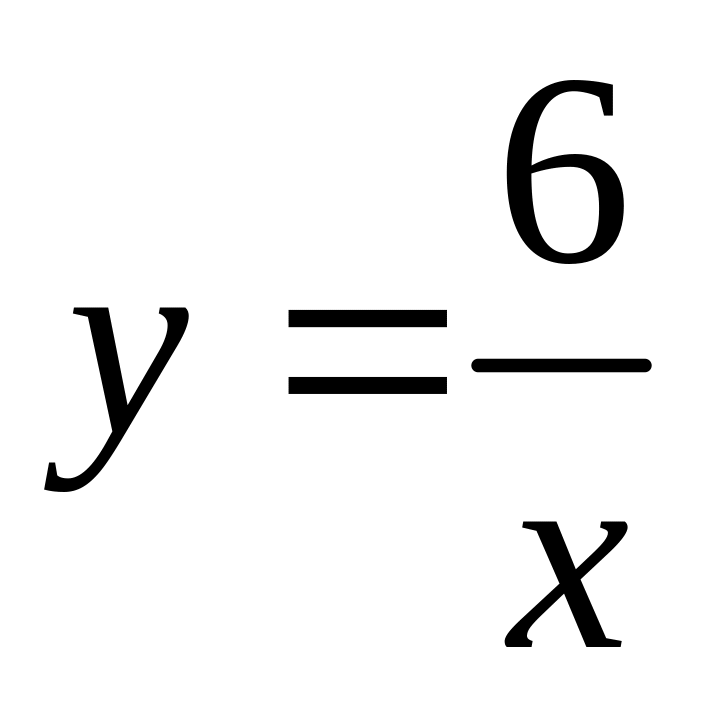 ,
прямыми
,
прямыми
![]()
![]() и осью
.
Сделать рисунок.
и осью
.
Сделать рисунок.
№ 9.
Вычислить объем тела, полученного
вращением вокруг оси
фигуры,
ограниченной линиями
![]() .
Сделать рисунок.
.
Сделать рисунок.
№ 10.
Вычислить объем тела, полученного
вращением вокруг оси
фигуры,
ограниченной линиями
![]() .
.
№ 11. Вычислить несобственные интегралы или установить их расходимость:
1)
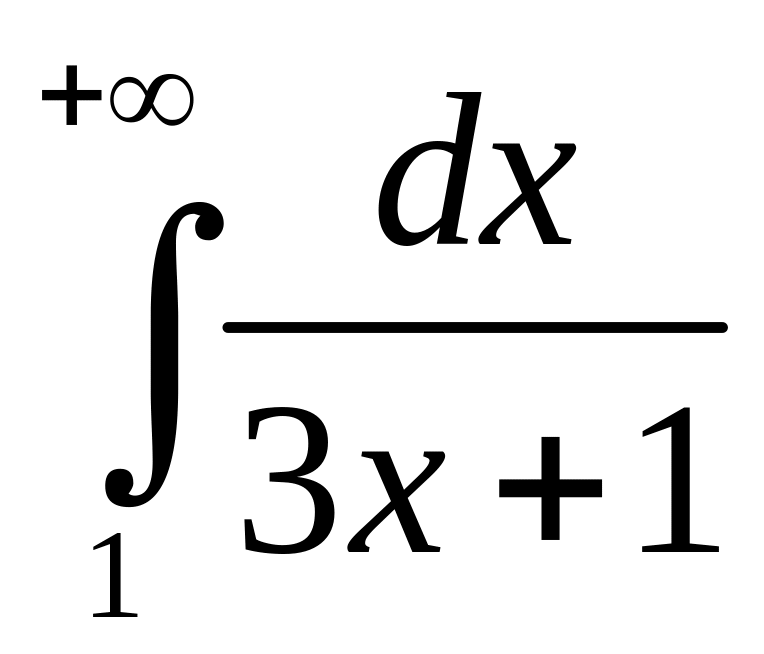 ;
;
2)
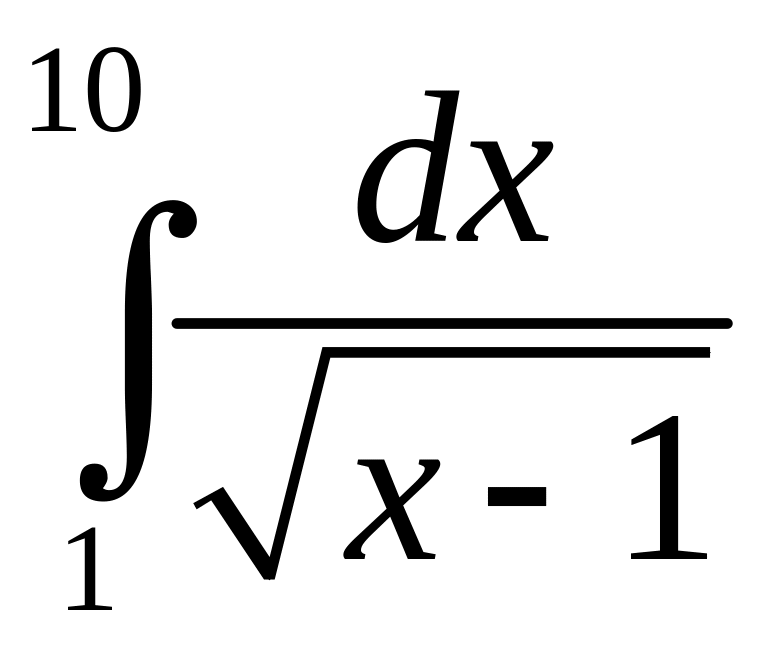 .
.
Защита РГР проводится письменно.
Максимальное количество баллов за защиту РГР: 7.
Общее максимальное количество баллов за РГР: 19.