Учебники / Введение в демографию

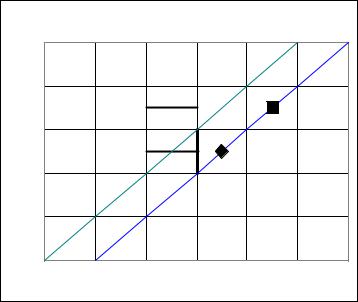
жизни людей, которые родились в t–3 году. Таким образом, прогнозируемая численность населения состоит из людей, которые 1 января года t находились в возрасте х полных лет и объединялись отрезком AB. Эта численность населения (обозначим ее, соответственно, Pm,x,t) и послужит нам базой для прогноза.

Рис. 20.2 Метод передвижки на сетке Лексиса

Очевидно, прогнозируемая численность населения Pm,x+1,t+1 отличается от базовой численности населения Pm,x,t, поскольку некоторая ее часть не доживет до 1 января t+1 года. Строго говоря, прогнозируемая и базовая численности населения связаны следующим уравнением:

где qm,x+1/2,t — вероятность того, живой мужчина, достигший точного возраста х+1/2 лет в середине года t, не доживет до середины года t+1 (на сетке Лексиса линия жизни такого мужчины прервется на отрезке, ограниченном точками Y и Z).

Выражение (1−qm,x+1/ 2,t ) используется в уравнении (20.8), так как

средний возраст в совокупности людей, которым в предыдущий день рождения исполнилось х полных лет (то есть в базовой численности населения), составляет х+1/2 года.

473

Поскольку точка Z принадлежит t +1 году, данными за который мы не располагаем на момент построения прогноза, постольку выражение

мы заменяем на приблизительно равное:

где Lm,x+1,t, Lm,x,t — соответственно, числа живущих в возрастах х+1 и х лет, рассчитанные для мужского населения в году t (на сетке Лексиса этим чис-

лам соответствуют отрезки GH и EF).

Соотношение (Lm,x+1,t / Lm,x,t ) получило название коэффициента пе-

редвижки, а процедура, применяющая данное соотношение, — метода передвижки возрастов.

Для прогноза численности мужского населения в возрасте 0 лет в году t +1 ( Pm ,0, t+1 ) используется следующая формула:

где Nm,t — число мальчиков, родившихся в период от середины года t

средний возраст людей, которым в середине года t +1 было меньше 1 года, составляет 1/2 года. Аналогично уравнению (20.9), мы можем заменить правую часть уравнения (20.10) на приблизительно равную:

где Lm,0,t — число живущих в возрасте 0 лет, рассчитанное для мужского населения в году t; lm,0,t – корень таблицы смертности, рассчитанной для мужского населения в году t.

Чтобы рассчитать величину Nm,t, необходимы данные об общих числах родившихся в годы t и t+1:

где Nt–1/2 и Nt+1/2 — числа родившихся в календарные годы t и t+1 (символы t–1/2 и t+1/2 обозначают, что учитываемые рождения произошли, соответ-

ственно, до середины года t и после середины года t+1); δm — доля маль-

чиков в общем числе родившихся; fx,t–1/2 и fx,t+1/2 — возрастные коэффици-

енты рождаемости в календарные годы t и t+1; Pf,x,t и Pf,x,t+1 — численности женского населения в возрасте х в годы t и t+1, соответственно.

474

Исходя из того, что возрастные коэффициенты рождаемости за один календарный год изменяются мало, уравнение (20.12) можно записать следующим образом:

где MIGRm,x+1,t+1, MIGRm,0,t+1 — сальдо миграции мужского населения, пе-

по формулам (20.14) и (20.15) могут быть итеративно повторены необходимое число раз. На практике, однако, значительно чаще используется другой способ — с применением более широких возрастных групп. При этом все возрастные группы (кроме наиболее старшей) должны быть одинаковой «ширины», а срок прогнозирования за одну итерацию должен быть равен «ширине» возрастных групп:

где n — ширина используемых возрастных групп и срок прогнозирования

до х+n лет в середине года t; nMIGRm,x+n,t+n — сальдо миграции мужского населения, пережившего середину года t+n в возрасте от х до х+n лет,

за период с середины года t до середины года t+n; nNt — число родившихся за период с середины года t до середины года t+n; n fx,t — возрастной коэффициент рождаемости в группе от х до x+n лет за период с середины года t до середины года t+n.

Смысл уравнений (20.16)–(20.18) состоит в том, что при отсутствии внешней миграции разность между численностью населения в возрасте х

475

лет и старше в году t и численностью населения в возрасте х+n лет и старше в году t+n равна числу смертей, произошедших за период с года t до года t+n среди лиц, которым в году t исполнилось х и более лет. Чтобы определить общее число смертей за указанный период, необходимо дополнительно учесть смертность детей, родившихся за период с t до t+n года.

Прогноз на срок, продолжительность которого отличается от величины кратной «ширине» используемых возрастных групп (например, на срок 12 лет при 5-летних возрастных группах), может быть получен интерполяцией прогнозов на стандартные сроки (в указанном случае — на сроки 10 и 15 лет). Такая интерполяция может быть произведена с помощью какойлибо из математических моделей (линейного, геометрического или экспоненциального роста). Другой способ (при наличии численности населения и коэффициентов дожития по одногодичным возрастным интервалам) состоит в нескольких итерациях прогноза сроком в 1 год.

Основное преимущество метода компонент (когортно-компонентного метода) заключается в возможности прогнозирования возрастно-половой структуры населения (для прогноза численности женского населения применяются уравнения, аналогичные уравнениям (20.8) – (20.18), используемым для прогноза численности мужского населения). Перспективные оценки возрастно-половой структуры населения служат основой для функциональных прогнозов населения.

Вставка 20.4. При прогнозе возрастно-половой структуры населения с учетом изменения его образовательного уровня применяется расширенный когортнокомпонентный метод. Для реализации данного метода необходимы исходные данные о возрастно-половой и образовательной структурах населения, а также предположения о будущих уровнях рождаемости, смертности и миграции населения. Расширенный когортно-компонентный метод предполагает отсутствие дифференциации смертности по уровню образования (United Nations, 1985). Построенный таким методом прогноз состоит из двух частей:

•население в возрасте 30 лет и старше по 5-летним возрастным группам, полу и уровню образования;

•население в возрасте до 30 лет по однолетним возрастным группам и полу

На методе компонент основывается и такой метод прогнозирования числа и структуры домохозяйств как «метод коэффициентов глав домохозяйств» (United Nations, 1989). В соответствии с этим методом, число домохозяйств, возглавляемых лицом, которое принадлежит к возрастной группе a и полу s, в году t+n (n, как правило, кратно 5 годам) составляет H s,a,t+n :

476

где Ps,a,t+n — прогнозируемая методом компонент численность населения,

принадлежащего к полу s и возрастной группе a в году t+n; HRs,a,t+n — коэффициент глав домохозяйств, равный отношению числа глав домохо-

зяйств, принадлежащих к полу s и возрастной группе a, к общей численности населения данного пола и возраста.

Предположения относительно будущих изменений коэффициентов глав домохозяйств строятся методом экстраполяции, исходя из анализа имеющихся данных, или ad hoc, учитывая тенденции изменения типов брачного поведения (в первую очередь — среднего возраста вступления в первый брак), величины семейных доходов, темпов жилищного строительства и т.д.

Полученные данные о числе домохозяйств H s,a,t+n могут суммиро-

ваться по полу главы домохозяйства и его возрасту, в том числе для прогноза среднего размера семьи AHSt+n :

a s

Результаты прогноза численности, структуры и среднего размера домохозяйств также имеют важное значение для разработки функциональных прогнозов.

20.5.КАУЗАЛЬНЫЙМЕТОД

Всовременной демографии используется еще один метод построения прогнозной модели, непосредственно примыкающий к математическому методу и получивший название каузального метода. Он предназначен для прогноза отдельных показателей воспроизводства населения (рождаемости, смертности и др.) как результата изменения их социально-экономических детерминант. Прогнозные модели, основанные на данном методе, описываются эконометрическими уравнениями и применяются в качестве составных частей сложных динамических моделей, а также для уточнения моделей, основанных на методе компонент. Целесообразность такого уточнения вызвана тем, что метод компонент предполагает неизменность параметров модели (чисел доживающих и возрастных коэффициентов рождаемости) или их изменение вне модели, а средне- и долгосрочные прогнозы предполагают существенное изменение условий жизни.

Ввиду различного назначения прогнозов, специфики применяемых концептуальных подходов и ограничений, накладываемых наличием статистических данных, в прогнозных моделях, основанных на каузальном ме-

477

тоде, используются различные комбинации социально-экономических детерминант.

Рассмотрим наиболее известные прогнозные модели, основанные на каузальном методе.

В модели «Мир-3» (Meadows et al., 1972), предназначенной для отражения взаимосвязанных изменений численности населения, объема производства, состояния окружающей среды и запаса природных ресурсов, выделен демографический блок, в котором население разделено на 4 возрастные группы: 0–14 лет (P1); 15–44 лет (P2); 45–64 лет (P3); 65 лет и старше (P4). Динамика численности этих групп описывается дифференциальными уравнениями, построенными на основе метода компонент и переменной (N), изменение которой прогнозируется с помощью каузального метода:

где N — общее число рождений; Qe,i — вероятность умереть в i-том возрастном интервале.

В свою очередь число рождений (B) зависит от численности женщин в репродуктивном возрасте (половина численности населения в возрасте 15–44 лет — P2) и величины суммарного коэффициента рождаемости:

где TFR — суммарный коэффициент рождаемости; MTF — физиологический максимум суммарной рождаемости; FCE — эффективность контроля над рождаемостью; DTF — желаемый уровень суммарной рождаемости.

Таким образом, если DTF превышает MTF, то TFR равен MTF. Если DTF ниже MTF, то TFR равен их среднему взвешенному, где весами служит FCE. При этом, если FCE=1, то суммарный коэффициент рождаемости равен DTF, а если FCE=0, то — MTF.

478

Вставка 20.5. Три перечисленных фактора суммарного коэффициента рождаемости также имеют свои детерминанты:

где η — константа физиологического максимума суммарной рождаемости, равная 12; Ne — компонент физиологического максимума суммарной рождаемости, нелинейная зависимость которого от ожидаемой продолжительности жизни e0 описывается выпуклой вверх возрастающей кривой (при e0=20 лет — Ne=0,4; при e0=40 лет — Ne=0,8; при e0=60 лет — Ne=1,0 при e0=80 лет — Ne=1,1 (см. Егоров и др. 1980, с. 49)); δ — константа «нормального» желаемого уровня суммарной рождаемости, равная 4; NI — «социальная норма размера семьи», нелинейная зависимость которой от среднедушевого уровня промышленного производства 20-тилетней давности I описывается выпуклой вниз убывающей кривой (при I=200 долл. США в ценах 1968 г. — NI=1,0; при I=400 долл. — NI=0,9; при I=600 долл. — NI=0,8 (см. Егоров и др., 1980, С. 49)); NW — «реакция средней семьи на социальную норму размера семьи», нелинейная зависимость которой от темпов изменения обеспеченности промышленной продукцией W за предшествующие 3 года описывается возрастающей ломаной линией (при W=(-2%) — NW=0,5; при W=0% — NW=0,7; при W=2% — NW=1,0 (см. Егоров и др. 1980, С. 50)); Me — «коэффициент, учитывающий младенческую смертность», нелинейная зависимость которого от ожидае-

мой продолжительности жизни 20-тилетней давности e0,20 описывается выпуклой вниз убывающей кривой (при e0,20=20 — Me=1,625; при e0,20=40 — Me=1,3;

при e0,20=60 — Me=1,1; при e0,20=80 — Me=1,0 (см. Егоров и др., 1980, С. 48)); MΩ —

показатель эффективности услуг планирования семьи, нелинейная зависимость которого от произведенных 20 лет назад инвестиций в производство средств контрацепции в расчете на душу населения Ω20 описывается выпуклой вверх возрастающей кривой (при Ω20=0,5 долл. — MΩ=0,85; при Ω20=1,0 долл. — MΩ=0,9;

при Ω20=2,0 долл. — MΩ=0,98; при Ω20=3,0 долл. — MΩ=1,0 (см. Егоров и др., 1980, С. 51)).

Вероятности умереть в i-том возрастном интервале (Qe,i) находятся в нелинейной зависимости от ожидаемой продолжительности жизни при рождении (e0). Так, Qe,1 приблизительно составляет 0,058 при e0=20; 0,037 — при e0=30;

при e0=20; 0,037 — при e0=30; 0,026 — при e0=40; 0,013 — при e0=50; 0,004 —

при e0=70; 0,001 — при e0=80. Qe,4 приблизительно составляет 0,123 — при e0=20; 0,069 — при e0=50; 0,04 — при e0=80 (см. Егоров и др., 1980, С. 49).

В свою очередь, ожидаемая продолжительность жизни при рождении рассчитывается по формуле:

где e0,b — базовая величина ожидаемой продолжительности жизни, равная 28 годам; LMF — коэффициент влияния уровня питания; LMHS — коэффициент «эффективного» (с 20-летним лагом) влияния медицинского обслуживания; LMC — коэффициент влияния городского образа жизни; LMP — коэффициент влияния загрязнения окружающей среды.

Вставка 20.6. LMF нелинейно зависит от уровня питания F, определяемого как отношение среднедушевого производства продовольствия к величине прожиточного минимума в зерновом эквиваленте, равной 230 кг /чел·год (при F=1 —

LMF≈0,635; при F=2 — LMF≈1,205; при F=3 — LMF ≈1,295; при F=4 — LMF≈1,365; при F=5 — LMF ≈1,409 (см. Егоров и др., 1980, С. 51)). LMHS нелиней-

но зависит от HS — уровня расходов на здравоохранение в расчете на душу населе-

ния (при HS=20 долл. — LMHS≈1,38; при HS=60 долл. — LMHS≈1,82; при HS=80 долл. — LMHS≈1,93; при HS=100 долл. — LMHS≈2 (см. Егоров и др., 1980,

С. 51)); LMC=1–U I , где U — коэффициент влияния урбанизации, нелинейно зависящий от численности населения P (при P=4 млрд. чел. — U=0,4; при P=6 млрд. чел. — U=0,525; при P=8 млрд. чел. — U=0,6; при P=12 млрд. чел. — U=0,725 (см. Егоров и др., 1980, С. 51)), а I — коэффициент влияния индустриализации, нелинейно зависящий от промышленного производства на душу населения Y (при

Y=0 — I≈0,5; при Y=200 долл. — I≈0,025; при Y=400 долл. — I≈–0,1; приY=600 — I≈– 0,063; при Y=800 — I≈–0,013; при Y=1200 — I≈0,1; при Y=1600 — I≈0,2 (см. Егоров и др., 1980, С. 51)); LMP нелинейно зависит от Z — отношения фактического уровня загрязнения к уровню загрязнения 1970 г. (при Z=0 — LMP=1; при Z=20 — LMP≈0,96;

при Z=30 — LMP≈0,94; при Z=50 — LMP≈0,85; при Z=80 — LMP≈0,55; при Z=90 — LMP≈0,4; приZ=100 — LMP≈0,2 (см. Егоров и др., 1980, С. 50)).

Очевидно, что вычисления, основанные на модели «Мир-3», отличаются значительной трудоемкостью. Эта модель не может быть использована на уровне отдельной страны и, тем более, ее региона. Наконец, тот факт, что между социально-экономическими и демографическими показателями существуют как прямые, так и обратные нелинейные (к тому же, зачастую, с временным лагом) связи, существенно усложняет интерпретацию результатов вычислений.

Более простые прогнозные модели, основанные на каузальном методе, использованы в моделях семейства Bachue, разработанных по инициативе Международной Организации Труда в рамках основанной ею Всемирной Программы Занятости в конце 1970-х — начале 1980-х гг.

В модели Bachue-Phulippines (Rodgers et al., 1978), брутто-

коэффициент воспроизводства населения (GRR) рассчитывается на основе регрессионного уравнения, параметры которого получены на основе анализа данных по 47 развивающимся странам:

GRRt = bi – 0,0064Rt-1 + 0,0106It-1 – 0,0446e0,t-1 + 0,0059Lt-1 , (20.26)

480

где bi — константа, характеризующая городское или сельское население; Rt-1 — доля занятых среди женщин в возрасте 15–44 лет в предшествующий период; It-1 — доля неграмотных среди взрослого населения в предшествующий период; e0,t-1 — ожидаемая продолжительность жизни при рождении в предшествующий период; Lt-1 — доля занятых в аграрном секторе в предшествующий период.

Ожидаемая продолжительность жизни при рождении в модели Bachue-Phulippines вычисляется по формуле:

где Y — ВВП на душу населения в долларах США; G — коэффициент Джини.

В модели Bachue–International (Moreland, 1984), построенной на основе данных по 25 странам и представляющей собой генерализацию моделей данного семейства, то есть сохраняющей базовые параметры взаимосвязей, описанных в частных моделях, специальный коэффициент рождаемости (FR) и ожидаемая продолжительность жизни (e0) вычисляются по формулам:

LOW40 — доля доходов, приходящаяся на 40 наименее богатых процентов населения; DRS — численность врачей на душу населения.

Каузальная модель Д. Уилера, построенная на основе эконометриче-

для прогноза, причем прогноза изменений величины показателей воспроизводства населения. Так, изменение специального коэффициента рождаемости (∆FR) в 1960–1977 гг. оценивается по формуле, рассчитанной на основе данных по 62 странам:

где ∆w — изменение доли женщин в возрасте 25–34 лет в численности женщин в возрастной группе 15–49 лет; ∆cdr — изменение общего коэффициента смертности; ∆y — процентное изменение величины ВВП на душу населения; plan — специальный индекс планирования семьи Молди-

на-Берельсона (см. Mauldin and Berelson, 1978).

481

Изменение общего коэффициента смертности в 1960–1977 гг. определяется уравнением, полученным на основе анализа данных по 64 странам:

цент населения в возрасте 0–14 лет; p50+ — процент населения в возрасте 50 лет и старше; t-1 — исходный момент времени.

К сожалению, модель Д. Уилера включает ряд редко используемых (индекс Молдина-Берельсона) и недостаточно надежных (общий коэффициент смертности) показателей, что существенно снижается ее практическую значимость, во всяком случае — применительно к экономически развитым странам и странам, возрастная структура которых подвержена периодическим колебаниям.

Существенный интерес представляют каузальные модели семейства ESCAP (разработанные в рамках деятельности Экономической и Социальной Комиссии ООН для Азии и Тихого океана) для Индонезии, Южной Кореи, Малайзии, Филиппин и Таиланда. Среди них наибольшего внимания заслуживают модели рождаемости, построенные на основе данных по Таиланду и Филиппинам, тогда как остальные модели рождаемости, а также смертности страдают определенными статистическими погрешно-

стями (см. Bilsborrow, 1989).

Модель рождаемости для Таиланда базируется на сопоставлении данных по его 72 провинциям за 1980 г. и оценивает приближение к некоему пороговому значению, округленно соответствующему уровню простого

где TFR — суммарный коэффициент рождаемости; SED — доля населения со средним и выше образованием; Y — ВВП на душу населения.

Модель рождаемости для Филиппин базируется на анализе связанных изменений социально-демографических переменных за 1957–1977 гг.:

где GMFR — коэффициент брачной рождаемости; Yp — среднедушевой личный доход; IMR — коэффициент младенческой смертности; RPF — относительная цена продуктов питания.

В целом каузальные модели представляют собой попытки количественного описания процесса демографического перехода. Несмотря на использование различных комбинаций экзогенных переменных, они относятся к четырем основным группам:

482