Учебники / Введение в демографию

РАЗДЕЛ VII. ДЕМОГРАФИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ

ГЛАВА 20 ПРОГНОЗЫ НАСЕЛЕНИЯ

20.1. ПОНЯТИЕ, НАЗНАЧЕНИЕИТИПЫПРОГНОЗОВНАСЕЛЕНИЯ

Прогнозы населения — научно обоснованная информация о будущих тенденциях изменения численности, параметров воспроизводства и структур населения на местном (региональном), национальном и глобальном уровнях. Прогнозы населения — важнейшая прикладная составляющая демографии, имеющая ключевое значение для экономики, государственного управления и научных исследований, наиболее очевидное обоснование необходимости исследований в области воспроизводства населения.

Первые приблизительно верные оценки перспективной численности населения появились задолго до становления демографии как науки о закономерностях воспроизводства населения. В настоящее время прогнозы населения наиболее часто используются в следующих, нередко взаимосвязанных случаях:

•при определении потребностей в продовольствии, энергии, жилье, соци- ально-бытовых, медицинских, образовательных, транспортных и других услугах (прогноз численности населения и отдельных возрастно-половых групп);

•при разработке программ социального, пенсионного и медицинского страхования (прогноз возрастно-половой и семейной структур населения, включая соотношение численности населения в трудоспособном и нетрудоспособном возрастах);

•при разработке национальных и региональных программ развития, отраслевых планов и планов размещения отдельных экономических объектов (прогноз численности населения, отдельных социально-демографических групп и показателей воспроизводства населения);

•при разработке политики народонаселения и/или программ человеческого развития (прогноз численности населения, отдельных социальнодемографических групп и показателей воспроизводства населения);

•при определении темпов экономического роста (прогноз численности населения (занятых), его образовательной, возрастно-половой и семейной структуры);

463

•при определении емкости рынка определенных товаров и услуг (прогноз численности отдельных социально-демографических групп, прогноз уровня рождаемости, смертности и брачности населения);

•при разработке моделей развития (в том числе футурологических), проведении научных исследований (прогноз численности населения, отдельных со- циально-демографических групп и показателей воспроизводства населения);

•при оценке состояния окружающей среды (прогноз численности населения и отдельных социально-демографических групп);

•при формировании избирательных округов и проведении выборных кампаний (прогноз численности населения и отдельных социальнодемографических групп).

Перечисленные случаи не исчерпывают всех возможностей примене-

ния прогнозов населения. При этом обращает на себя внимание то, что в современных условиях прогноз населения — это прежде всего предположение о перспективах изменения структуры населения. Отсюда не следует, что прогнозы численности населения утратили свою актуальность. Дело в том, что усложнение современного общества, рост многообразия человеческой деятельности требуют оценок изменения все более разнообразных социально-демографических структур. Кроме того, замедление темпов роста численности населения (а в ряде стран — переход к стадии стабилизации) приводит к тому, что изменения структур населения (главным образом, вследствие старения населения, приобретающего глобальный характер, а также миграции населения) становятся ведущим фактором демографической динамики.

Разнообразие задач, решаемых с помощью прогнозов населения, обусловливает существование многих видов таких прогнозов. Наибольшее значение имеют классификации прогнозов населения по их назначению, по длине периода прогнозирования, по количеству объектов прогнозирования, по типу представления прогнозируемой величины и по методу построения (см. Араб-Оглы, 1978; Бахметова, 1982).

По своему назначению прогнозы делятся на реалистические (прогнозируемые величины близки к действительности), аналитические (прогнозируемые величины отражают результаты каких-либо действий — например, преодоления смертности от какой-либо причины) и прогнозы-предостережения (прогнозируемые величины характеризуют перспективы, которых следует избегать).

По длине периода прогнозирования выделяются краткосрочные (до

5 лет), среднесрочные (на 5–20 лет) и долгосрочные (на 20–50 лет) прогнозы.

По количеству объектов прогнозирования различаются единичные (изменения одной переменной) и множественные (изменения двух или более переменных) прогнозы.

464

В зависимости от типа представления прогнозируемой величины прогнозы могут быть точечными (величина представлена одним числом) или интервальными (величина представляется в интервале показателей или в виде различных вариантов).

Выделяются прогнозы, построенные математическим методом (прогнозируемая величина описывается единой функцией от своего базового значения и переменной времени), методом компонент (прогнозируемая величина является результатом изменений ее составляющих, описываемых различными функциями) и казуальным методом (прогнозируемая величина является зависимой переменной в эконометрическом уравнении, связывающем эту величину с ее социально-экономическими детерминантами).

20.2. ОБЩИЕПРИНЦИПЫПОСТРОЕНИЯПРОГНОЗОВНАСЕЛЕНИЯ

Любой прогноз населения строится по определенной процедуре, включающей следующие этапы (см. Hinde, 1998):

1)выбор прогнозной модели, описывающей будущее изменение населения (сценарий изменения показателей воспроизводства населения);

2)определение параметров выбранной прогнозной модели;

3)применение выбранной прогнозной модели к исходным фактическим показателям.

Воснове выбора прогнозной модели лежит гипотеза будущего изменения демографических процессов, формулирующаяся с учетом избранного срока прогнозирования. Как правило, такая гипотеза в отношении возрастных показателей рождаемости, смертности и миграции разрабатывается не на каждый год прогнозного периода, а на моменты, называемые опорными годами прогноза (показатели на промежуточные годы определяются интерполяцией).

Один из способов разработки гипотезы — прогноз на основе исторических аналогий — основывается на сопоставлении тенденций воспроизводства населения в стране, для которой строится прогноз, и стране, опережающей первую в демографическом развитии (например, в долгосрочной перспективе развивающимся странам предстоят изменения демографических процессов, аналогичные происходящим в настоящее время в экономически развитых странах). Успех такого способа зависит от того, насколько точно выбрана «опережающая» страна и как соотнесены скорости изменения демографических процессов.

Второй способ разработки гипотезы — трендовый прогноз. В основе этого способа лежит экстраполяция выявленных тенденций. При этом следует иметь в виду две существенные проблемы. Во-первых, прогнозист, как правило, не допускает неопределенно долгое сохранение в будущем тех

465

тенденций, которые в исходный период имеют негативный характер (например, рост смертности от какой-либо причины). В этом случае может быть определен период допустимости трендового прогноза. Во-вторых, простая экстраполяция существующих тенденций (например, снижения показателей смертности) технически может привести к тому, что вероятность смерти окажется отрицательной, что противоречит здравому смыслу. Для решения этой проблемы необходимо ввести дополнительные ограничения или прогнозировать не вероятность смерти, а ее логитпреобразование (см. Валентей, 1991, С. 234–235).

Третий способ — прогноз на основе суммарных характеристик. На-

пример, на основе показателя ожидаемой продолжительности жизни и типовых таблиц смертности (см. Меликьян, 1994, С. 526–529) прогнозируются возрастные коэффициенты смертности. Для прогноза суммарных оценок могут использоваться специальные методики. Так, гипотеза изменений уровня смертности может разрабатываться на основе концепции эндогенной и экзогенной смертности, модели Брасса (см. Меликьян, 1994, С. 30). Гипотеза изменений уровня рождаемости — на основе когортного анализа плодовитости, модели Бонгаартса (см. Меликьян, 1994, С. 26–27).

Четвертый способ — нормативный прогноз — предполагает изменение показателей воспроизводства населения в результате каких-либо усилий общества. Например, уровень смертности в каком-либо возрасте может снижаться вследствие полной или частичной элиминации смертности от отдельной причины (см. Кваша, Ионцев, 1995, С. 154–169).

Пятый способ — прогноз на основе экспертных оценок — учитывает мнение специалистов (причем в самых широких областях науки) о наиболее вероятных тенденциях изменения демографических процессов в будущем. Данный метод предполагает тщательный отбор экспертов, разработку специальных анкет для их опроса и методики обработки полученных данных.

Выбор прогнозной модели в значительной степени связан с методом построения прогноза, зависящим от его назначения, необходимой детализации (общая численность населения, численность населения по укрупненным возрастным группам или численность населения по пяти- / однолетним возрастным группам) и наличия исходных статистических данных. Чем более определенно, специфично назначение прогноза, чем более он детализирован, чем полнее и подробнее исходные данные, тем более целесообразен выбор прогнозной модели, основанной на более трудоемком и точном методе компонент.

Существенное значение имеет и срок прогнозирования. На коротких временных отрезках, как правило, не происходит существенных изменений уже сложившихся демографических тенденций, поэтому, например,

466

для краткосрочного прогноза общей численности населения приемлемую точность может обеспечить и экстраполяция. При долгосрочном прогнозировании, напротив, целесообразно предусмотреть возможность, при определенных условиях, существенного изменения тенденций воспроизводства населения.

При построении прогнозов используются два вида данных: исходные демографические показатели (фактические данные, служащие базой для построения прогноза) и параметры модели (описывающие предстоящие изменения населения). Определение параметров модели — наиболее сложная проблема в рамках построения прогноза, так как нет возможности наверняка утверждать, какие изменения ожидают население в будущем. После того, как выбрана прогнозная модель, точность прогноза будет зависеть от величины параметров модели. Для их уточнения традиционно применяются следующие приемы:

•приближение закономерностей, описываемых параметрами, к реальным закономерностям (например, выявленным на ограниченном временном промежутке);

•оценка чувствительности прогнозируемых значений к изменению параметров (от уточнения параметра можно отказаться в случае, когда прогнозируемая величина мало зависит от изменения параметра);

•разработка многовариантного прогноза, в котором различные варианты строятся на различных значениях параметров (среди этих вариантов вы-

деляется основной, считающийся наиболее правдоподобным, и аналитические, отражающие вариацию величин параметров).

Таким образом, прогнозы населения всегда характеризуются условностью, определяемой методом построения прогноза и выбранными значениями параметров. Рассмотрим подробнее методы построения прогнозов.

20.3.МАТЕМАТИЧЕСКИЙМЕТОД

Воснове математического метода (также называемого формульным) лежит использование единой формулы, характеризующей изменение населения в целом (или какой-либо демографической группы) без учета изменений его составляющих. На математическом методе построены, в частности,

модели экспоненциального роста и модели логистического роста.

По существу, прогнозирование с помощью математического метода сводится к экстраполяции данных на базе функции, параметры которой определены по изменениям населения в прошедший период.

Общее уравнение модели экспоненциального роста выглядит следующим образом:

467

в год t (на который строится прогноз); e — основание натуральных логарифмов; r — среднегодовой темп роста численности населения (постоянный на весь период прогнозирования).

Дифференцируя уравнение (20.1) по переменной t , получим уравнения для величины среднегодового темпа роста численности населения:

Вставка 20.1. На экспоненциальной модели роста основано и так называемое «правило 70», позволяющее предсказать период, за который при постоянном темпе роста произойдет удвоение исходной численности населения:

T ≈ 70/ R ,

где T — период удвоения; R — среднегодовой темп роста численности населения в процентах ( R =100r ).

«Правило 70» имеет несложное обоснование:

P0 er T = 2 P0 , ln 2 = ln(e r T ) ,

T = lnr2 = 0,693r ≈ 70r .

Аналогичным образом может быть выведено и «правило», позволяющее определить время утроения исходной численности населения:

P0 erΨ = 3 P0 , ln3 = ln(e r Ψ) ,

Ψ = lnr3 = 1,099r ≈ 110r ,

где Ψ — период утроения; R — среднегодовой темп роста численности населения в процентах.

Отличительная особенность экспоненциальной модели роста состоит в том, что она характеризует изменение численности населения как непрерывный процесс, отражая реальность рождений и смертей на всем протяжении года. В этом и состоит принципиальное отличие экспоненциальной

468

модели от модели роста в геометрической прогрессии (использованной, например, Т.Р. Мальтусом), при которой изменение численности населения рассматривается как одномоментное (по итогам года) событие:

Уравнения (20.1) и (20.4) связаны следующим образом. Рассмотрим численность населения в год ( t =1 ):

P1 = P0 (1+ r) .

Допустим, что изменение численности населения в течение года представляет собой сумму j изменений. Тогда:

P1 = P0 (1+ r / j) j .

Если j очень велико ( j → +∞), то lim(1+ r / j) j = er . Отсюда,

P1 = P0 er ,

P2=P1 er = (P0 er ) er = P0 e2r , Pt = P0 er t .

Для практического применения экспоненциальной модели необходимо определить один параметр — среднегодовой темп роста ( r ) — на основе фактических данных о численности населения ( Pt ). В этих целях

может быть использована линейная регрессия, уравнение которой получено логарифмированием уравнения (20.1):

ln Pt = ln P0 + rt .

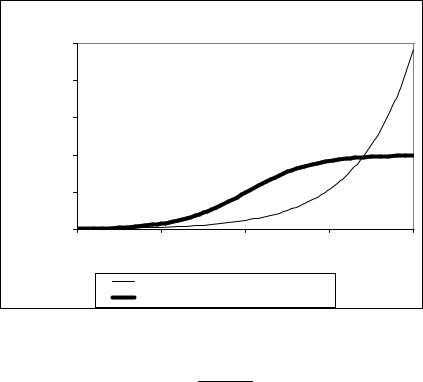
Основной недостаток экспоненциальной модели роста состоит в том, что при неизменном темпе роста численность населения увеличивается безгранично (если r > 0 ) или достигает нуля (если r < 0 ). Однако такая динамика численности нереалистична, по крайней мере, в течение длительного времени (см. рис. 20.1), что существенно ограничивает возможности применения экспоненциальной модели.

Чтобы повысить реалистичность прогнозируемой динамики населения, в XIX в. была разработана модель логистического роста, в которой темп роста численности населения определенным образом (через параметр k ) зависит от численности населения. Внесем необходимые изменения в уравнение (20.3):

469

Отсюда,

где C — константа, определенным образом связанная с изменением численности населения за прошедший период; k — параметр уравнения, рассчитываемый так, что отношение ( r / k ) выражает величину, к которой стремится численность населения в модели логистического роста (верхнюю асимптоту логистической кривой).

Уравнение (20.6) может быть представлено и в другой форме:

где K = r / k , α = ln(C K) , β = −r .

Для практического применения логистической модели необходимо определить три параметра: K, α, β . Параметр K (первоначально верхняя

асимптота логистической кривой определялась как «предельная численность

470

населения», которая может быть обеспечена продуктами питания при наилучшем использовании земель) вычисляется по следующей формуле:

где Pi , Pi+n , Pi+2n — фактическая численность населения за три года, раз-

деленных двумя равными и достаточно продолжительными (например, 50 лет) промежутками времени.

Отсюда могут быть определены отношения κ ( κ = Pt / K ) во все годы, для которых известна численность населения:

e−α−βt

κ = (1+ eα+βt )−1 = (1+ e−α−βt ) .

Логарифмируя, получаем уравнение линейной регрессии для определения параметров α и β:

ln (κ/(1-κ)) = –α – βt

Для повышения точности прогнозов по экспоненциальным и логистическим моделям роста необходимо определение параметров моделей на основе данных о численности населения за как можно большее число точек наблюдения. Минимальное число точек наблюдения должно быть на одну больше числа параметров модели.

В конце XX в. логистическая модель продолжает использоваться при разработке пронозных гипотез изменения рождаемости и смертности, однако в прогнозах общей численности населения применяется все реже и реже ввиду того, что социальная обусловленность процессов воспроизводства населения требует построения демографического прогноза на основе метода компонент.

Вставка 20.2. К математическому методу относятся и другие модели:

•модель линейного роста (при постоянной величине абсолютного прироста δ, например, в результате миграции): Pt = P0 (1+δt);

•параболическая модель (при изменении абсолютного прироста на постоянную величину): Pt = P0 + bt + ct2;

•модели вероятности дожития px (зависящей от причин, несвязанных с возрастом

(параметр A0), и ослабления жизнеспособности организма (параметр B0)), основанные на показательной функции: lg px = A0 + B0 cx.

471

20.4. МЕТОДКОМПОНЕНТ

Метод компонент (когортно-компонентный) рассматривает динамику численности населения как результат изменения ее составляющих — чисел рождений, смертей, чистого числа мигрантов, — каждая из которых прогнозируется по отдельности. В принципе, для оценки числа рождений и смертей могут быть использованы общие коэффициенты рождаемости и смертности. На практике, однако, это происходит сравнительно редко, так как перечисленные коэффициенты напрямую зависят от возрастно-половой структуры населения, а в качестве параметров прогнозной модели применяются возрастные и специальные коэффициенты.

Вставка 20.3. Метод компонент может быть применен и для прогноза численности какой-либо социально-демографической группы. При этом, чем детальнее определена такая группа, тем большее число процессов должно быть учтено при построении прогноза. Так, простейший метод прогнозирования численности семей, разработанный канадским ученым У. Иллингом, учитывает:

•число семей в исходный момент времени (H0), определяемое по результатам переписи населения;

•число браков, заключаемых в течение периода прогнозирования (UT), определяемое, исходя из гипотезы изменения уровня брачности;

•число разводов, совершаемых в течение периода прогнозирования (ET), определяемое, исходя из гипотезы изменения уровня разводимости;

•число умерших в течение периода прогнозирования среди состоящих в браке (WT), определяемое, исходя из гипотезы изменения уровня смертности;

•сальдо миграции семей в течение периода прогнозирования (МT), определяемое, исходя из гипотезы изменения миграции.

Отсюда, прогнозируемое число семей (Ht) равно: Ht = H0 + UT – ET – WT + МT.

Допустим, нам предстоит построить методом компонент прогноз численности мужского населения в возрастной группе х+1 лет на 1 января

t+1 года (Pm,x+1,t+1) в стране, где отсутствует внешняя миграция. При прогнозировании мы можем использовать данные о численности мужского

населения по возрастам и показатели таблицы смертности мужского населения за предыдущий год.

Обратимся к сетке Лексиса (см. рис. 20.2), чтобы выяснить, где на ней находится население, численность которой нам предстоит прогнозировать. Речь идет о совокупности населения, находящейся на пересечении вертикальной линии, соответствующей 1 января t+1 года, и горизонтальной полосы, соответствующей возрасту х+1 исполнившихся лет, — то есть о вертикальном отрезке CD.

В то же время отрезок CD лежит на пересечении горизонтальной полосы х+1 исполнившихся лет и диагональной полосе включающей линии

472