Учебники / Введение в демографию

Для расчетов функции возрастной структуры c(x) стабильного населения следует использовать дискретное приближение формулы (18.3):

Вставка 18.1. Пусть население разбито на τ-летние возрастные группы. Доля каждой возрастной группы в общей численности населения будет равна сумме всех

0

После ряда преобразований подынтегральной функции получается расчетная формула (18.5).

При r = 0 из формулы (18.4) получается возрастная структура стационарного населения:

τ

c(x, x + τ) = n ∫l(x +t)dt .

0

Из формулы (18.3) следует, что возрастная структура зависит от двух переменных: порядка вымирания l(x) и одного из двух взаимосвязанных

коэффициентов — общего коэффициента рождаемости и коэффициента естественного прироста. При этом, чем выше, при прочих равных условиях, коэффициент естественного прироста или общий коэффициент рождаемости, тем ниже доля лиц старших возрастов в общей численности насе-

ления. Эта зависимость отражена на рис. 18.2. Режим смертности трех популяций, расположенных в верхней части рисунка, определяется функцией дожития типовой таблицы смертности ООН с ожидаемой продолжительностью жизни при рождении для двух полов, равной 40 лет. Популяции различаются по коэффициентам прироста населения. Видно, что самая молодая возрастная структура наблюдается у населения с наибольшим коэффициентом естественного прироста, равным r = 2% , самая старая — у стационарного населения ( r = 0 ). Аналогичная закономерность наблюдается у трех нижних популяций с низким уровнем смертности. Режим

433

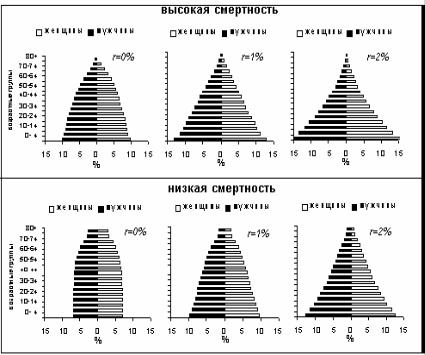
смертности в данном случае задается типовой таблицей смертности ООН с ожидаемой продолжительностью жизни при рождении для двух полов, равной 70 годам. Из рисунка 18.2 видно, что при одном и том же уровне естественного прироста те популяции, где продолжительность жизни выше, имеют более низкую долю детских и более высокую долю старших возрастов в общей численности населения.

Рис. 18.2. Возрастные пирамиды стабильных популяций с высокой ( e0жен. = 40 ) и низкой ( e0жен. = 70 ) смертностью и истинным

коэффициентом прироста r = 0%,1%, 2% .

18.5.РЕАЛЬНОЕИУСЛОВНОЕПОКОЛЕНИЯ

ВСТАБИЛЬНОМНАСЕЛЕНИИ

Из свойства изменения числа родившихся в стабильном населении по экспоненциальному закону следует, что численность реального поколения в модели стабильного населения больше предыдущего и меньше по-

434

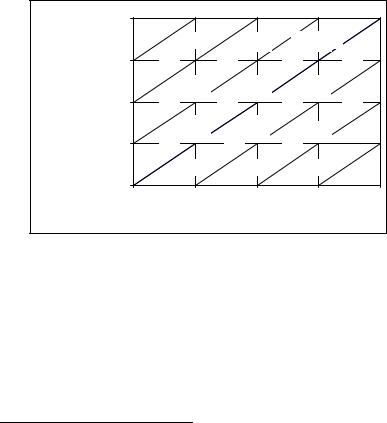
следующего в er раз1. Эта же величина определяет соотношение между численностями соседних возрастных групп в условных поколениях. Последнее утверждение вытекает из формулы (18.3). Соотношения значений родившихся, умерших и численности всего населения для условных и реальных поколений стабильного населения можно отобразить на сетке Лексиса (см. рис. 18.3). При этом из определения стабильного населения следует, что в нем интенсивности рождаемости и смертности реального и условного поколений для одних и тех же возрастов совпадают.

18.6.ИСТИННЫЕКОЭФФИЦИЕНТЫИРЕЖИМВОСПРОИЗВОДСТВА

Умодели стабильного населения имеется одно фундаментальное свойство, которое объясняет ее мощные аналитические возможности. Оно заключается в том, что каждой комбинации возрастных распределений смертности l(x) и рождаемости f (x) соответствует единственное стабильное населе-

ние с определенной возрастной структурой, общими коэффициентами рождаемости и смертности, а также коэффициентом естественного прироста.

1 Если рассматривается дискретная модель, т.е. изменение численности населения и числа родившихся происходит по закону геометрической прогрессии, то отношения между двумя соседними поколениями и двумя соседними возрастными группами составят (1+ r) раз.

435

Как уже отмечалось, одним из самых распространенных приемов демографического анализа является проекция на будущее современных параметров воспроизводства населения. Зафиксировав имеющиеся реальные интенсивности рождаемости и смертности, можно оценить различные параметры этого населения после стабилизации: общие коэффициенты рождаемости и смертности, коэффициент естественного прироста, нетто-коэффициент воспроизводства, характеристики возрастной структуры и некоторые другие. Совокупность количественных характеристик стабильного населения (истинные коэффициенты рождаемости, смертности, естественного прироста, нетто-коэффициент воспроизводства, характеристики возрастной структуры и некоторые другие), генерированных функциями рождаемости и смертности некоторого реального населения, определяет режим воспроизводства этого населения. При этом заданные функции рождаемости и смертности называют экзогенными параметрами режима воспроизводства, а все остальные расчетные величины относятся к эндогенным параметрам.

Полученные показатели модели затем сравниваются с показателями реального населения. При этом они могут заметно отличаться друг от друга. Однако показатели стабильного населения в отличие от реального обладают важным преимуществом. Общие коэффициенты рождаемости и смертности, коэффициент естественного прироста стабильного населения свободны от влияния возрастной структуры. Поэтому с их помощью, освободившись от влияния значимого структурного фактора, можно лучше понять демографическую специфику данного периода. По этой причине коэффициенты стабильного населения назвали истинными коэффициентами соответственно рождаемости, смертности и естественного прироста.

18.7. ИНТЕГРАЛЬНОЕУРАВНЕНИЕВОСПРОИЗВОДСТВАНАСЕЛЕНИЯ

(ИУВ)

Одним из возможных математических выражений процесса смены поколений в стабильном населении (для одного пола) является интегральное уравнение воспроизводства (или уравнение Лотки), которое описывает тра-

дений N(t) зависит от численности женщин в репродуктивных возрастах,

т.е. от числа девочек, рожденных 15–50 лет тому назад. Дети, родившиеся x лет назад и численность которых равна N(t − x) , с вероятностью l(x)

доживут до момента t . Вероятность рождения ребенка в возрастном интервале от x x до x + dx у тех, кто дожил до момента t , определяется

436

функцией f (x)dx . Таким образом, для всех возрастов от α =15 до β = 50 можно записать:

α

С помощью интегрального уравнения были выведены многие свойства стабильного населения и получены оценки его основных параметров. Так,

заменяя в уравнении (18.6) N (t) равной величиной N(0) er x , а N(t − x)

на величину N(0) er (t−x) , а затем сокращая на N(0) er t , можно получить

характеристическое уравнение стабильного населения с неизвестным коэффициентом естественного прироста r :

∞

∫e−r x f (x)l(x)dx =1.

0

Это уравнение имеет бесконечно много комплексных корней и единственный действительный корень r , который является истинным коэффи-

циентом естественного прироста стабильного населения или коэффици-

ентом Лотки. Поэтому каждой комбинации возрастных распределений функции дожития l(x) и функции рождаемости f (x) соответствует един-

ственное стабильное население с присущими ему одному возрастной структурой, общими коэффициентами рождаемости и смертности, а также коэффициентом естественного прироста r .

Уравнение (18.6) называют однородным интегральным уравнением воспроизводства. Однако, если изучается реальное население, в котором процесс стабилизации начался в некоторый момент времени, то при исчислении N (t) следует ввести поправку G(t) , отражающую вклад исходного

женского населения в процесс рождаемости. Тогда получаем уравнение Лотки в неоднородной форме:

α

При t ≥ β функция G(t) равняется 0 , поскольку все женщины, жив-

шие в момент t = 0 , выходят из репродуктивного возраста. Отказываясь от предположения о неизменности функций рождаемости и смертности в уравнениях (18.6) и (18.7), можно получить однородное и неоднородное интегральные уравнения, описывающие процесс воспроизводства любого населения.

437

18.8.ВЫЧИСЛЕНИЕИСТИННЫХКОЭФФИЦИЕНТОВ

ВСТАБИЛЬНОМНАСЕЛЕНИИ

Лотка вычислил истинный коэффициент естественного прироста, решая характеристическое уравнение (18.8):

где l(x) — вероятность для женщин дожить от рождения до возраста x ;

r — истинный коэффициент естественного прироста в расчете одного человека; f (x) — функция рождаемости, т.е. вероятность рождения девочек

и женщины (или мальчиков у мужчин поскольку, напомним, речь идет

ют, что α =15, а β = 50 годам), то мы можем подставить значения α и β

в качестве пределов определенного интеграла. При r = 0 стабильное население превращается в стационарное.

На практике достаточно хорошее приближение к действительному

Функции R0 , R1 и R2 называют, соответственно, нулевым, первым и

вторым моментами. В терминах возрастных коэффициентов рождаемости и смертности по τ-летним возрастным группам формулы для R0 , R1 и R2

имеют вид:

Решая квадратное уравнение (18.9) относительно r и подставляя значения (18.10), получим выражение для действительного корня:

R0 в формуле (18.11) представляет собой нетто-коэффициент воспро-

изводства (NRR), который показывает, в какой пропорции материнское поколение замещается дочерним. Условно принимая численность дочернего поколения равной 1, основываясь на формуле роста численности стабильного населения (1) можно записать:

где T — период смены поколений или длина поколений. Отсюда можно получить следующие приближенные формулы для r :

Под средней длиной поколения T в демографии понимают средний интервал времени, разделяющий поколения родителей и их детей (матерей и дочерей, отцов и сыновей). В стабильном населении средняя длина поко-

ления T определяется как интервал времени, в течение которого численность поколения изменятся в R0 раз. Этот интервал, как следует из форму-

2

возрастного интервала.

439

Значения этого показателя, как правило, находятся в интервале от 25 до 30 лет.

Существует другой способ оценки длины поколения в стабильном насе-

В таблице 18.1 приведены этапы вычисления истинного коэффициента естественного прироста по формуле (18.12) с использованием данных Госкомстата для женского населения России за 1989 г. Отметим, что оценка коэффициента Лотки по формуле (18.15) равна — 0,198% и незначительно отличается от полученного в таблице 18.1 результата.

Табл. 18.1. Вычисление истинного коэффициента естественного прироста для женского населения России по данным Госкомстата 1989 г.

r = −0,00196 или −0,196% в год.

440

18.9. ИСТИННЫЕ КОЭФФИЦИЕНТЫ РОЖДАЕМОСТИ И СМЕРТНОСТИ

Истинные коэффициенты рождаемости и смертности представляют собой коэффициенты, которые будут достигнуты в населении в конце периода стабилизации, т.е. это коэффициенты рождаемости и смертности стабильного населения.

Истинный коэффициент рождаемости можно выразить следующей формулой:

Хорошей аппроксимацией для формулы (18.16) служит выражение:

Очевидно, что истинный коэффициент смертности равен разности истинного коэффициента рождаемости и истинного коэффициента естественного прироста:

в табл. 18.1, возрастные показатели таблиц смертности для России 1989 г. и формулу (18.5)1, можно рассчитать возрастную структуру стабильного женского населения. Соотношение полов при рождении, равное 1,05 мальчика на 1 девочку, позволяет при том же коэффициенте естественного прироста и показателях таблиц смертности для мужчин найти также и возрастную структуру стабильного мужского населения. В табл. 18.2 приведены

1 Формула (18.5) используется в модифицированном виде, поскольку оцениваются численности отдельных возрастных групп P(x, x + τ) , а не их доли в общей чис-

ленности населения, т.е. P(x, x + τ) = N L(x, x + τ) e−r (x+2,5) .

441

вычисления, иллюстрирующие данную процедуру. В целях корректности сопоставления возрастных структур различных стабильных населений, их численность приводят к величине, кратной 10, например, 10000 или100000. Последний столбец табл. 18.2 дает распределение населения, исходя из общей численности в 100000 человек. Он получен с помощью умножения значений в столбцах (6) и (7) на поправочный коэффициент равный 100000/(7218695 + 6877705) .

Найдем истинные коэффициенты рождаемости и смертности. Сумма всех элементов колонки (7), представленное в строке «всего», равно 6877705. При этом число рождений девочек принимается равным 100000 (радикс женской таблицы смертности). Таким образом, коэффициент рождаемости на 1 женщину равен 100000/ 6877705 = 0,01454 или 14,54 на 1000

женщин. Аналогично для мужского населения: разделив число рождений мальчиков 105000 на 7218695 (строка «всего» столбца 6) получим 0,01455 или 14,55 на 1000 мужчин. Общий коэффициент рождаемости стабильного

Общий коэффициент смертности стабильного населения составляет

14,54 −(−1,96) =16,5 на 1000 населения.

18.11. ПРИЛОЖЕНИЯМОДЕЛИСТАБИЛЬНОГОНАСЕЛЕНИЯ

Модель стабильного населения широко используется в аналитических целях. В ее терминах определяются многие демографические индикаторы, в первую очередь система показателей режима воспроизводства. На практике для оценки сложившейся демографической ситуации широко используется метод сравнения параметров реального и стабильного населения. С помощью модели стабильного населения исследуются разнообразные теоретические проблемы, изучение которых на основе наблюдений за реальными данными затруднено. В первую очередь это относится к изучению взаимосвязей между возрастной структурой и процессами смертности и рождаемости. Включение в модель миграции позволяет узнать, каким образом миграционные процессы влияют на процесс воспроизводства населения.

На основе модели стабильного населения разработаны методы получения, восстановления или коррекции информации в условиях неполных или недостоверных данных. Возможности исследователей здесь были существенно расширены благодаря разработке французским демографом Буржуа-Пиша (1958) модели квазистабильного населения.

442