
Учебники / Введение в демографию
.pdfВо втором случае из экспоненциального закона демографического роста вытекает 2 P(0) = P(0) er T . Логарифмируя левую и правую части, легко получить, что период удвоения для непрерывного случая равен:
T = |
ln2 |
. |
(16.12) |
|
|||
|
r |
|
|
Вычисление периода удвоения в демографических, финансовых и экономических расчетах известно также как «правило 70». Натуральный логарифм 2 равен 0,6931… или округленно 0,7. Тогда в непрерывном слу-
чае период удвоения будет равен T = 0,7/ r |
или T = 70/(100 r) , если выра- |
|
зить прирост населения в процентах (т.е. |
100 r ). |
В дискретном случае |
для получения «правила 70» надо заменить |
величину ln(1+θпр) |
|
ее приближенным значением θпр . |
|
|
16.11. МЕНЯЮЩАЯСЯСКОРОСТЬДЕМОГРАФИЧЕСКОГОРОСТА
Пусть коэффициенты прироста населения меняются на протяжении периода (0,τ) таким образом, что на каждом временном интервале ∆t ( ∑∆t = τ)
наблюдаются различные, постоянные на этих интервалах, темпы прироста населения r0,r1,r2,… . Тогда численность населения в конце периода может
быть представлена следующим экспоненциальным выражением:
P(τ) = P(0) er0 ∆t er1 ∆t er2 ∆t …= P(0) er0 ∆t +r1 ∆t +r2 ∆t +….
Если ∆t — бесконечно малая величина, то сумма показателей степени является интегралом функции r(t) и численность населения в момент τ
равняется:
τ |
|
|
∫r(t)dt |
|
(16.13) |
P(τ) = P(0) e0 |
. |
16.12. ЛОГИСТИЧЕСКАЯМОДЕЛЬДЕМОГРАФИЧЕСКОГОРОСТА
Увеличение населения по экспоненциальному закону может продолжаться до бесконечности. Очевидно, подобная динамика возможна тогда, когда никакие факторы природного или социального порядка не ограничивают этот рост. В реальности экспоненциальный рост наблюдается на ограниченном временном интервале. Поэтому уже в XIX веке проводились поиски «закона», который бы отражал факт сдерживания экспоненциального
413
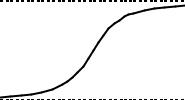
роста населения по мере увеличения его численности. Так, известный бельгийский физик А. Кетле, опираясь на примеры из физики, предполагал, что «сопротивление росту населения должно возрастать пропорционально квадрату скорости этого роста». В дальнейшем бельгийский математик П. Ферхюльст (1838) реализовал эту гипотезу в математической форме в виде кривой, которую он назвал «логистической». Затем его открытие было практически предано забвению до 1920 г., когда американские ученые Р. Пирл и Л. Рид вновь ввели логистическую кривую в научный оборот для описания роста численности популяций в биологии и демографии человека.
Математически логистическая функция выражается формулой
P(t) = |
K |
, |
1+eα−r t |
где P(t) — численность населения в момент t ; e — основание натуральных логарифмов; K, α, r — параметры уравнения логистической кривой.
Графически логис- |
|
|
|
|||
|
|
|
||||
тическая фунция пред- |
|
|
|
|||
ставляется |
|
в |
виде |
|
|
|
S-образной, или сигмо- |
|
|
|
|||
идной, |
|
|
кривой |
|
|
|
(см. рис. 16.2). |
|
Пара- |
|
|
|
|
метр K |
определяет |
|
|
|
||
положение линии (аси- |
|
|
|
|||
мптоты), |
задающей |
|
|
|
||
максимально |
|
воз- |
|
|
|
|
|
|
|
|
|||
можную |
или |
|
педель- |
Рис. 16.2 Криваялогистического ростанаселения |
||
ную численность насе- |
||||||
ления при данных условиях. Его можно трактовать как меру «емкости среды» для особей данного вида. Величина этого параметра, как показали демографические исследования, например, для США, увеличивается со временем. Подобное увеличение пределов роста ученые связывали с растущей емкостью среды обитания человека благодаря научно-техническому прогрессу.
414
Вставка 16.4. Гиперболическая модель роста населения Земного шара
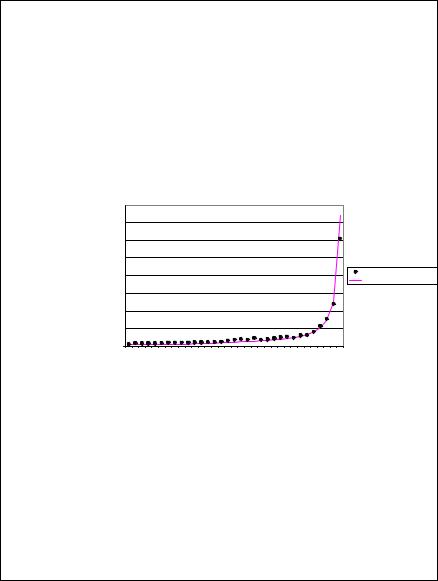
Попытки найти модель, описывающую динамику численности населения всей Земли за длительный период времени, привели некоторых ученых, среди которых можно назвать известного физика академика С. Капицу, к заключению, что демографические данные за много поколений хорошо укладываются только на гиперболическую кривую. На основе анализа демографических данных была получена простая формула, соответствие которой реальным данным показано на рисунке 16.3:
|
|
|
|
|
|
|
P = C /(T1 −T ) =186 /(2025 −T ) , |
|
|
||||||||||||
где P — число людей на земле в момент времени T |
(млрд. чел.); T1 — крити- |
||||||||||||||||||||
ческая дата; C — постоянная C с размерностью (человеко-годы). |
|||||||||||||||||||||
Однако |
ги- |
8000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
перболическая |
7000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
модель вызывает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
целый |
|
ряд |
во- |
6000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
просов |
|
среди |
5000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
которых |
|
выде- |
4000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оценки Бюро Цензов (США) |
|||
ляются два. |
Во- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболическая модель |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
первых, |
|
|
чис- |
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ленность |
насе- |
2000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ления |
по |
|
мере |
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
приближения к |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
критической |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
00 |
-300 -100 |
00 |
0 |
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
||||||
|
|
|
|
|
400 600 80 |
1000 |
120 |
30 |
1400 |
50 |
0 |
1700 |
80 |
0 |
2000 |
||||||
дате |
обращает- |
-5 |
2 |
16 |
|
19 |
|
||||||||||||||
|
|
|
|
1 |
1 |
|
1 |
|
|||||||||||||
Рис. 16.3 Гиперболическаямодельростанаселениямира |
|||||||||||||||||||||
ся в |
бесконеч- |
||||||||||||||||||||
ность. |
Получа- |
|
|
|
|
|
|
(млн. чел.) |
|
|
|
|
|||||||||
ется, что 2025 год является подобием конца света. Во-вторых, согласно этой модели можно прийти к другому абсурдному результату, что люди жили в далеком прошлом, например, 10 или 20 млрд. лет тому назад.
В целях преодоления этих трудностей С. Капица установил границы роста числа людей по гиперболе, как в прошлом, так и в настоящем. Минимальная граница определяется условием, что скорость роста не может быть менее одного человека за поколение. Максимальная граница определяется тем, что по мере приближения к критической точке в силу вступают факторы, ограничивающие демографический рост. Скорость роста численности населения не становится очень большой. Она проходит через максимум в период демографического перехода. По мере того, как скорость демографического роста уменьшается, население Земли выходит на плато и стабилизируется. Гиперболический закон изменения численности населения перестает действовать.
415
ЛИТЕРАТУРА
Основная
1.Капица С. Сколько людей жило, живет и будет жить на Земле. Очерки теории роста человечества. М., 1999.
2.Курс демографии под ред. Боярского А.Я. М..
Дополнительная
1.Капица С. Математическая модель роста населения мира // Математическое моделирование. М., 1992. Т 4, № 6.
2.Keyfitz N. Applied Mathematical Demography. N.-Y., 1985.
3.Капица С.П. Теория роста населения Земли. М., 1997.
416

ГЛАВА 17 МОДЕЛЬ СТАЦИОНАРНОГО НАСЕЛЕНИЯ
ИЕЕ ПРИЛОЖЕНИЯ
17.1.ОПРЕДЕЛЕНИЕСТАЦИОНАРНОГОНАСЕЛЕНИЯ
Вглаве, посвященной анализу смертности, было дано определение таблиц смертности как численной модели вымирания поколения. Вместе с тем существует и другая, несколько отличная от «поколенной», интерпретация этих таблиц, согласно которой таблицы смертности задают некоторое теоретическое население, не подверженное влиянию миграционных процессов. В этом закрытом населении порядок смертности, числа рождений и возрастная структура полностью определяются соответствующими показателями таблицы смертности и являются постоянными величинами. Поскольку все демографические параметры такого населения, включая его общую численность, не изменяются со временем, оно было названо стационарным, что в переводе с латинского (stationarius) означает неподвижный.
Итак, стационарное |
население — это теоретическое население |
с неизменными числами |
рождений и возрастными характеристиками |
смертности, определяемыми таблицей смертности.
Вставка 17.1. В демографическую науку понятие стационарного населения было введено английским ученым Э. Галлеем еще в конце XVII века. С помощью модели стационарного населения им был разработан наиболее популярный в XVIII–XIX вв. метод построения таблиц смертности, получивший названия «метод смертных списков» или «метод Галлея». В конце XIX в. немецкий статистик Г. Кнапп детально изучил основные количественные соотношения в стационарном населении. В современной демографической науке модель стационарного населения рассматривается в рамках разработанной А. Лоткой теории стабильного населения (см. главу «Модель стабильного населения и ее применение»). Здесь стационарное население является частным случаем стабильного населения при условии равенства нулю величины естественного прироста населения.
Модель стационарного населения расширяет круг приложений таблиц смертности за пределы изучения смертности. С помощью модели стационарного населения могут решаться не только демографические, но и самые разнообразные экономические задачи, такие как, например, анализ движения кадров на предприятии, особенности формирования автомобильного парка города, планирование расходов в области социального обеспечения. Все эти задачи объединяет то, что, во-первых, подлежащие изучению совокупности состоят из элементов, которые выбывают из них через определенное время и, следовательно, обладают такой характеристикой, как про-
417

должительность жизни в данной совокупности. Во-вторых, количество этих элементов и их распределение по возрасту предполагается неизменным или почти неизменным во времени. Разработанные более трех столетий тому назад таблицы смертности превратились из чисто демографического в один из общенаучных методов исследования.
17.2. ТАБЛИЦЫСМЕРТНОСТИИМОДЕЛЬСТАЦИОНАРНОГО НАСЕЛЕНИЯ
Для того, чтобы построить модель стационарного населения, надо оценить функции таблицы смертности. Возрастные коэффициенты смертности стационарного населения определяются соответствующей функцией m(x) таб-
лиц смертности. Возрастная структура стационарного населения задается табличной функцией L(x) . Именно в интерпретации этой функции модель
стационарного населения отличается от модели вымирания поколений. В таблицах смертности L(x) обозначает число человеко-лет, прожитых в ин-
тервале теми, кто достиг возраста x . В модели стационарного населения этот показатель определяет численность соответствующей возрастной группы. Поэтому второе название L(x) — число живущих в стационарном насе-
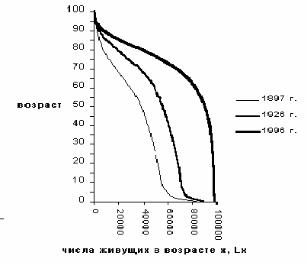
лении в возрасте x . На рис. 17.1 представлены числа живущих в стационарном населении для женского населения России, полученные из таблиц смертности за 1896-1897, 1926 и 1996 гг. Если поменять оси координат местами, то мы фактически получим кривые дожития соотвествующих таблиц смертности. Из графиков видно, что чем выше продолжительность предстоящей жизни, тем больше численность стационарного населения.
Поскольку функция L(x) , как и другие функции таблиц смертности,
по условиям построения модели неизменна, постольку постоянной является и возрастная структура стационарного населения. Общая численность стационарного населения соотвественно равна сумме всех
ω
L(x) , т.е. T = ∑L(x) . Здесь ω — предельный возраст таблиц смертности.
0
Аналог этого показателя в таблицах смертности T (0) интерпретируется
как общее число человеко-лет, которое проживут все новорожденные. Доля отдельной возрастной группы в общей численности стационарного
населения составляет c(x) = TL((0x)) .
Число умерших в отдельных возрастных группах стационарного населения выражается функцией d(x) . Общее число родившихся в течение
418
года в стационарном населении равно корню таблицы смертности l(0) .
Общий коэффициент смертности в стационарном населении равен
|
ω |
|
|
|
|
∑d(x) |
|
l(0) |
|
m = |
0 |
; общий коэффициент рождаемости равен n = |
. |
|
T (0) |
|
|||
|
|
T (0) |
||
Рис. 17.1 Числа живущих в стационарном населении для женского населения России, за 1896-1897, 1926 и 1996 гг.
17.3. СВОЙСТВАСТАЦИОНАРНОГОНАСЕЛЕНИЯ
Остановимся на других свойствах стационарного населения, вытекающих из его определения:
ω
1) изравенствачислаумершихчислуродившихся, т.е. ∑d(x) = l(0) , следует:
0
а) естественный прирост стационарного населения равен нулю; б) общие коэффициенты рождаемости и смертности в стационарном
населении равны: m = n ;
в) (с учетом условия закрытости) общая численность стационарного населения неизменна во времени.
2) общие коэффициенты смертности и рождаемости обратно пропорциональны ожидаемой продолжительности предстоящей жизни
419
при рождении. Из определения ожидаемой продолжительности пред- |
||||||||||||
стоящей жизни при рождении e(0) = |
T |
|
и определений общих коэффи- |
|||||||||
|
|
|
|
|
|
l(0) |
|
|
|
|
|
|
циентов (см. свойство 3) следует |
n = m = |
|
1 . |
|
|
|
||||||
|
|
|
|
|
|
|
|
e(0) |
|
|
|
|
3) постоянство всех демографических показателей обусловливает идентичность |
||||||||||||
всех |
возрастных |
характеристик |
реального |
и |
условного |
поколений |
||||||
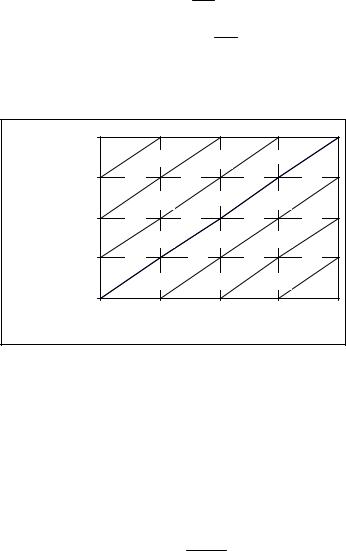
встационарномнаселении, чтохорошовиднонасеткеЛексиса(см. рис. 17.2). |
||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L4 |
|
|
L4 |
|
L4 |
|
|
|
|
|
3 |
l3 |
|
l3 |
|
|
|
l3 |
|
l3 |
|
|
|
|
|
L3 |
|
|
L3 |
|
L3 |
|
|
|
|
возраст |
2 |
l2 |
|
l2 |
|
|
|
l2 |
|
l2 |
|
|
|
|
|
L2 |
|
|
L2 |
|
L2 |
|
|
|
|
|
1 |
l1 |
|
l1 |
|
|
l1 |
|
l1 |
|
|
|
|
|
|
L1 |
|
|
L1 |
|
L1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
lo |
1 |
lo |
|
2 |
lo |
3 |
lo |
4 |
|
|
|
|
|
|
|
время |
|
|
|
|||
|
Рис. 17.2 Диаграмма Лексиса для стационарного населения |
|||||||||||
4) численность поколений в стационарном населении равна числу родившихся,
умноженному на |
среднюю продолжительность предстоящей |
жизни |
прирождении, т.е. |
= e(0) l(0) . Это свойство вытекает изопределения ожи- |
|
даемой продолжительности жизни и интерпретации функции T (x) |
вмодели |
|
стационарногонаселения.
5) средний возраст умерших стационарного населения равен ожидаемой продолжительности предстоящей жизни при рождении. Это свойство непосредственно вытекает из определения соответствующих показателей в таблицах смертности:
e(0) = ∑ω x d(x) , 0 l(0)
где x — средний возраст смерти в интервале (x, x +1) .
420
Средний |
возраст умерших |
в реальном населении |
отличается |
от ожидаемой |
продолжительности |
предстоящей жизни, |
поскольку |
он аккумулирует в себе колебания чисел родившихся и особенности возрастной структуры умерших, отличающейся от структуры умерших в стационарном населении.
17.4. ПРИЛОЖЕНИЯМОДЕЛИСТАЦИОНАРНОГОНАСЕЛЕНИЯ
Демографические исследования
В демографических исследованиях модель стационарного населения используется в нескольких направлениях Она является одним из средств сравнительного анализа демографических процессов и структур. Так, возрастная структура стационарного населения применяется в качестве стандарта для сравнения смертности методом стандартизации. На основе модели стационарного населения были также разработаны и систематизированы некоторые демографические показатели.
Модель стационарного населения применяется для изучения демографических характеристик реального населения. Очевидно, что в действительности не бывает населения, количественные характеристики которого бы полностью совпадали с параметрами стационарной модели. Для того, чтобы модель стационарного населения воплотилась в жизнь, необходимо, чтобы режимы смертности и рождаемости не изменялись в течение долгого периода времени при условии, что числа родившихся и умерших были равны друг другу при полном отсутствии миграции. Подобные требования невыполнимы применительно к человеческим популяциям. С определенной долей условности можно говорить о стационарном населении применительно к древним историческим популяциям, поскольку их численность изменялась чрезвычайно медленно на протяжении длительных исторических периодов. Однако при более детальном рассмотрении за этой «неподвижностью» скрываются значительные колебания в демографической динамике из-за эпидемий, голода, войн и вторжений чужеземцев. В современном мире в некоторых развитых странах уровень прироста населения на протяжении последних лет колеблется вокруг нулевой отметки. Но возрастная структура этих стран далека от стационарной, во-первых, из-за сохраняющегося влияния демографической волны, генерированной падением рождаемости в период второй мировой войны и последующим за ним бэби-бумом, во-вторых, из-за демографических тенденций последних десятилетий (колебаний в уровне рождаемости, продолжающегося снижения смертности и значительного притока иммигрантов).
421

Вместе с тем, как отмечал французский демограф Р. Пресса, «хотя соответствие между реальным населением и теоретическим стационарным населением никогда не может быть вполне строгим, все же в некоторых случаях такое сопоставление, поскольку оно допустимо, может дать некоторые полезные сведения»1. К проведению подобных оценок подталкивают особенности статистических данных, свойственных тому или иному историческому периоду, а также простота свойств модели стационарного населения. Так, в палеодемографических исследованиях, как правило, доступными данными являются числа умерших по отдельным возрастным группам, и неизвестными — данные о числах живущих. Гипотеза стационарности лежит в основе построения таблиц смертности по этому возрастному распределению умерших (метод смертных списков). Исходя из обратной зависимости между ожидаемой продолжительностью предстоящей жизни и общими коэффициентами рождаемости и смертности, можно получить вероятные комбинации этих показателей для исторических популяций, общий и естественный прирост в которых был в среднем близок к нулю. Если исходить из того, что наиболее вероятные значения средней продолжительности предстоящей жизни для отдельных государств и народов в прошлом находятся в интервале от 20 до 30 лет, то соответствующие им общие коэффициенты смертности и рождаемости (это следует из свойства 5) попадают в интервал от 30 до 50‰.
Недемографические исследования
Границы применения модели стационарного населения значительно расширятся, если мы расширим само понятие «население». Под «населением» можно понимать не только численность людей, проживающих на определенной территории, но и численность персонала на предприятиях, учащихся школ и вузов, клиентов страховых компаний и пенсионных фондов, пациентов больниц и др. Кроме человеческой популяции, существуют популяции в животном мире. Также можно говорить о «населении» применительно к различным совокупностям, состоящим из неодушевленных объектов: станочный парк, автомобильный парк, товары на складе и др. Многие из этих совокупностей в большей степени удовлетворяют условиям стационарности, чем реальные населения регионов и стран. В целом, совокупности, для которых можно построить модель стационарного населения (или таблицу смертности) обладают одним общим свойством. Выбытие элемента из совокупности, подобно смерти, представляет собой неповторяющееся событие, интенсивность которого зависит от возраста элемента.
1 Р. Пресса Народонаселение и его изучение / Пер. с фр. М., 1966.
422
