
Учебники / Введение в демографию
.pdfпределение рождений, смертей, браков, разводов и миграций. На основе этой информации можно рассчитать показатели уровня и календаря демографических процессов в данном календарном периоде.
6.5. ДЕМОГРАФИЧЕСКИЕПОКАЗАТЕЛИ
Демографический процесс в реальной или условной когорте характеризуется интенсивностью и распределением во времени соответствующих событий.
Абсолютные демографические показатели
Характеристику того или иного демографического процесса в населении можно начать с абсолютного числа демографических событий. Например, можно посмотреть, как менялось число смертей или число рождений в населении на протяжении определенного периода. Анализ абсолютного числа демографических событий основывается на уравнении демографического баланса:
|
P(t) = P(0) + {N(0,t) − M (0,t)}+ {I (0,t) − E(0,t)}, |
||
где P(0) |
и P(t) — численности населения в начале и в конце исследуемого |
||
периода; |
N (0,t) — число |
родившихся за период (0,t) ; |
M (0,t) — число |
умерших |
за период (0,t) ; |
I (0,t) — число иммигрантов |
за период (0,t) ; |
E(0,t) — число эмигрантов за период (0,t) .
Для анализа отдельных демографических процессов, однако, использование и сравнение одних лишь абсолютных чисел событий недостаточно ввиду изменения численности и структуры населения.
Покажем это на примере. Сравним рождаемость в двух странах, ис-
пользуя общие числа родившихся. Например, мы знаем, |
что в 1997 году |
|
в Китае родилось 21,02 млн. детей. |
В Бенине в том же |
году родилось |
274,4 тыс. детей. Можно ли сказать, |
что рождаемость в Китае выше, чем |
|
в Бенине? Скорее всего, нельзя, так как достаточно вспомнить, что численность населения Китая в 209,6 раза превышает численность населения Бенина, не говоря о других факторах, которые могут повлиять на общее число рождений. Для того чтобы устранить воздействие общей численности населения на показатели, характеризующие демографические процессы, можно рассчитать соответствующие общие коэффициенты.
Приведем еще один пример. Если в двух странах, одинаковых по численности населения, окажется также и равное число смертей, то еще нельзя говорить о том, что смертность в этих странах одинаковая. В одной стране большая часть зарегистрированных смертей — это смерти пожилого населения, в другой — молодого населения. То есть на величину абсолют-
113

ных чисел событий может также повлиять структура населения (в нашем примере — возрастная структура). Чтобы преодолеть ограниченные возможности абсолютных показателей, используются относительные характеристики интенсивности демографических процессов.
6. 5.1. Характеристики интенсивности демографического процесса
Для характеристики интенсивности демографических событий можно использовать вероятности наступления событий или коэффициенты.
Вероятность наступления демографического события — «относи-
тельная величина, характеризующая возможность наступления данного события для одного человека при условии, что все люди из данной когорты в равной мере подвержены риску этого события»1.
Вероятность наступления события в возрастном интервале рассчи-
тывается как отношение числа событий в данном интервале к численности той части когорты в начале интервала, для которой изучаемое событие еще не наступило. Например, если изучается вероятность вступления в первый брак, то необходимо разделить число браков в возрастном интервале на численность незамужних (неженатых) в начале интервала.
Пример: рассчитаем вероятность вступления в брак в интервале возраста от 15 до 16 лет. В точном возрасте 15 лет когорта состоит из 600 незамужних женщин. В возрасте 15 исполнившихся лет (то есть при переходе от точного возраста 15 лет к точному возрасту 16 лет) в этой когорте было зарегистрировано 60 первых браков. Чтобы получить вероятность вступления в первый брак в возрасте 15 исполнившихся лет, необходимо разделить число первых браков на численность когорты в начале интервала:
60/600=1/10.
В общем виде формула вероятности может быть записана следующим образом:
qx (k )= Pхy(xk(k−)1),
где qx (k ) — вероятность наступления события в возрасте х исполнившихся лет, то есть при переходе от точного возраста x к точному возрасту x +1; k — очередность изучаемого события; yx (k ) — число событий
винтервале возраста от х до x +1; Pх (k −1) — численность членов когорты
вначале интервала, не испытавших изучаемого события k.
При изучении вероятностей наступления демографических событий необходимо помнить о том, что их величина зависит от длины интервала: чем длиннее интервал, тем выше вероятность наступления изучаемого со-
1 Народонаселение. Энциклопедический словарь. М., 1994. С. 42.
114

бытия. Следовательно, можно сравнивать вероятности, относящиеся только к одинаковым временным интервалам. Например, нельзя сравнивать вероятность умереть в возрастных интервалах 5–9 лет и 10–19 лет. Чтобы сравнить интенсивность демографического процесса на разных интервалах времени, нужно сравнивать не вероятности, а коэффициенты.
Таблица единственного выбытия: если для некоторого временного интервала нам известны все вероятности qx = yx / Px , то, используя сле-
дующий алгоритм, можно построить таблицу, показывающую распределение неповторяющихся событий в изучаемой когорте:
yx = Px qx ,Px − yx = Px+1.
Такимобразом, мыполучаемтриосновныхраспределениятаблицы:
1.Px , распределение чисел «доживающих» до точного возраста х, то есть численность индивидов в точном «возрасте» х, не испытавших еще изучаемого неповторяющегося события;
2.распределение вероятностей qx испытать изучаемое событие меж-
ду точными «возрастами» х и x +1(или в «возрасте» x исполнившихся лет);
3. распределение неповторяющихся событий yx , наступивших
в интервале «возраста» х исполнившихся лет.
Еще одно распределение выводится из предыдущих. Это вероятность px не испытать изучаемое событие в данном интервале возраста. Оно рас-
считывается как дополнение до единицы вероятности qx :
|
px =1− qx . |
|
Таблица |
единственного выбытия |
наиболее часто используется |
в демографии, |
в частности, для анализа |
процесса смертности (о методах |
расчета таблиц смертности рассказано в главе 8). Таблицы единственного выбытия можно строить также при изучении любых других, помимо смертей, неповторяющихся событий: например, при анализе первых рождений или первых браков.
Коэффициенты интенсивности демографических процессов —
«среднее значение силы демографического процесса в данном интервале времени, взвешенное временем, прожитым всей когортой в данном интервале времени, например, числом человеко-лет, прожитых в этом интервале»1.
1 Народонаселение. Энциклопедический словарь. М., 1994. С. 155. 115

В отличие от вероятности, коэффициент относит число событий в интервале не к численности когорты в начале интервала, а ко времени, прожитому в данном интервале всеми членами когорты, дожившими до его начала.
При расчете коэффициентов на первый план выходит проблема знаменателя, поскольку нам необходимо соотнести число некоторых событий в населении, составляющих числитель, с тем населением в знаменателе, в котором эти события произошли. Собственно, вся система коэффициентов строится на основе перехода к знаменателям, в большей степени отражающим население, причастное к наступлению изучаемых событий.
В общем виде коэффициент представляет собой число демографических событий в наблюдаемом календарном периоде, отнесенное к среднему числу прожитых человеко-лет в данном периоде всеми индивидами, составляющими изучаемое население.
Пусть t — коэффициент, который нужно рассчитать; y — число демо-
графических событий; P — средняя численность населения за период; Т — длительность наблюдаемого периода.
Тогдакоэффициентвобщем видеможнорассчитать по формуле:
t = P yT .
Среднюю численность населения или среднее население рассчитывают, обычно используя формулу средней арифметической. Если численность населения в течение года колеблется не очень сильно, то можно ограничиться полусуммой начальной и конечной численности населения (на 1 января и 31 декабря). В том случае, если численность населения региона сильно различается по месяцам или сезонам, среднее население может быть рассчитано как сумма ежемесячных численностей населения, отнесенная к числу месяцев.
Как правило, коэффициенты рассчитываются приведенными к году, то есть за календарный период, равный одному году, при T =1.
Различают несколько видов демографических коэффициентов, характеризующих интенсивность демографических процессов: общие коэффициенты, специальные и повозрастные коэффициенты, суммарные коэффициенты.
Общий коэффициент показывает среднее число демографических событий, приходящееся на среднее число человеко-лет, прожитых в течение одного года изучаемым населением.
Если В — число браков в населении в течение года, P — средняя численность населения, b — общий коэффициент брачности, то
b = PB 1000 .
116

Например, |
в России |
в 1996 году |
было зарегистрировано |
|
866651 браков (В), |
средняя |
численность |
населения |
составила |
147739000 человек ( P ), общий коэффициент брачности был равен: 149739000866651 1000 = 5,9 ‰1.
Полученное значение (5,9‰) можно интерпретировать следующим образом:
–в населении России в 1997 году в среднем приходилось 0,059 браков на одного человека, или 5,9 браков на 1000 человек;
– если бы население России насчитывало только 1000 человек, то в нем было бы зарегистрировано 5,9 браков.
Что нам дает общий коэффициент по сравнению с абсолютной чис-
ленностью событий? Покажем это на примере (см. табл. 6.2). |
|
|
||||
|
Табл. 6.2. Сравнение абсолютного числа смертей |
|
|
|||
|
и общих коэффициентов смертности в России в 1926 и 1996 гг. |
|
||||
|
|
|
|
|
|
|
|
|
1926 |
|
|
1996 |
|
|
число смертей |
1920 |
тыс. |
|
2082,2 |
тыс. |
|
численность населения (на начало года) |
92735 |
тыс. |
|
147976 |
тыс. |
|
общий коэффициент смертности |
20,7‰ |
|
14,2‰ |
||
Источник: Население России за 100 лет (1897–1997). М.: Госкомстат, 1998.
Если принимать во внимание только число смертей, то можно было бы прийти к выводу, что смертность в России за 70 лет выросла. Общий коэффициент смертности свидетельствует об обратном: общая смертность за этот период снизилась, поскольку за тот же период численность населения росла более быстрыми темпами, чем число смертей. Таким образом, устраняя влияние общей численности населения, общий коэффициент на один шаг приближает нас к измерению настоящего уровня изучаемого процесса.
Вернемся теперь к общему коэффициенту брачности. В знаменателе этого коэффициента представлено все население, хотя в брак могут вступать только люди, достигшие установленного законом брачного возраста, и при этом не состоящие в браке, то есть бракоспособное население. Поэтому следующим шагом будет расчет специального коэффициента брачности, знаменатель которого более точно отражает то население, которое вступает в брак.
Специальный коэффициент представляет собой отношение числа зарегистрированных в течение года событий к среднему числу человеколет, прожитых в течение того же года населением, способным продуциро-
1 Общие коэффициенты обычно приводятся в промилле (‰), то есть в расчете на 1000 человек.
117

вать эти события. Например, специальный коэффициент брачности пред-
ставляет собой отношение числа зарегистрированных браков к средней численности бракоспособного населения (населения, достигшего брачного возраста и не состоящего в браке):
bспец = |
|
|
B |
. |
|
|
|
||
P |
||||
|
|
бракосп. |
|
|
Аналогично рассчитывается специальный коэффициент рождаемо-
сти: среднее число детей, рожденных женщинами в репродуктивном возрасте за прожитый год.
Специальный коэффициент элиминирует, таким образом, не только влияние общей численности населения, но и частично — влияние структуры населения, так как в знаменателе находится только то население, которое может продуцировать демографические события. Специальный коэффициент брачности можно рассчитывать также отдельно для мужчин и женщин.
В то же время нам известно, что в брак вступают преимущественно молодые люди. Поэтому можно предположить, что чем больше в населении пожилых, тем ниже будет коэффициент брачности. Чтобы избавиться от воздействия возрастной структуры на уровень демографического процесса, рассчитываются повозрастные коэффициенты.
Повозрастные коэффициенты представляют собой отношение числа демографических событий наступивших в течение года у индивидов определенного возраста х, к числу человеко-лет, прожитых данной возрастной
группой1 в том же году. Так, повозрастной коэффициент брачности женщин показывает среднее число браков в течение прожитого года у женщин в возрасте х:
bх = Bхf . Pх
Повозрастные коэффициенты дают возможность измерить уровень демографического феномена независимо от воздействия возрастной структуры. Когда повозрастные коэффициенты рассчитываются для однолетних возрастных интервалов, влияние возрастной структуры можно считать полностью устраненным, так как предполагается, что в течение одного года жизни демографические события распределены равномерно2. Если коэф-
1 Возрастные группы могут быть однолетними, пятилетними и др. в зависимости от исходных данных и целей исследования.
2 Напомним, что при изучении смертности это допущение неприменимо. В течение первого года жизни в экономически развитых странах младенческая смертность сконцентрирована на первой неделе и первом месяце жизни.
118
фициенты рассчитывают для пятилетних или десятилетних возрастных групп, определенное влияние возрастной структуры может сохраняться.
Числители у повозрастных коэффициентов и вероятностей одинаковые. Различаются только знаменатели. В общем виде формула повозрастного коэффициента может быть записана следующим образом:
|
|
t x |
= |
yx (k ) |
|
|
|
|
|
Pх+0,5 (k −1) |
|
|
|||
|
|
|
|
|
|
||
при |
условии |
равномерного |
|
распределения |
событий |
в интервале. |
|
Где yx (k ) — |
число событий |
|
очередности k |
в данном |
интервале; |
||
Pх+0,5 |
(k −1) — число человеко-лет, прожитых в данном интервале теми, |
||||||
кто не испытал события k.
Если события распределены в интервале неравномерно, то эта формула даст нам лишь приближенное значение коэффициента. Когда интервал не слишком велик, можно считать, что события распределены в интервале равномерно. Исключение составляет младенческая смертность и смертность в пожилых возрастах, что будет показано в соответствующей главе.
Соотношение между повозрастными коэффициентами
ивероятностями
Икоэффициенты, и вероятности используются для характеристики интенсивности демографических процессов в когорте. Тем не менее надо принимать во внимание, что расчет этих показателей приводит к разным числовым результатам. Эти различия вытекают из определения и формы расчета показателей. Покажем разницу на примере. Рассмотрим поколение женщин, в котором наступают только первые браки. Предположим, что смертность и миграция отсутствуют, а события в возрастных интервалах распределены равномерно.
Пусть известно |
B1x |
— |
число первых браков в возрасте |
x исполнившихся лет; |
P f , |
P f |
— число незамужних женщин в точных |
|
x |
x+1 |
|
возрастах х и x +1. Тогда для этого поколения женщин в данном интервале
мы можем рассчитать qx = |
B1x |
— вероятность вступить в первый брак |
|||
P f |
|||||
|
|
|
|
||
|
x |
|
|
|
|
в интервале точного возраста от х до x +1 и t x = |
B1x |
— коэффициент |
|||
P f |
|||||
|
|
|
|
||
|
|
|
x+0,5 |
|
|
первых браков в возрасте х при условии, что браки равномерно распреде-
119
лены в интервале возраста от х до x +1. В нашем примере длина интервала равна одному году. Если интервал более длинный (5 или 10 лет), то следует помнить, что коэффициент не зависит от длины интервала, и, напротив, чем длиннее интервал, тем будет больше значение вероятности вступления в первый брак.
Расчет повозрастных коэффициентов ставит нас перед необходимостью иметь дело с большим количеством чисел. В то же время для сравнений удобно пользоваться одним единственным числом. Как мы уже видели, общий и специальный коэффициенты непригодны для сравнений, так как зависят от воздействия структуры населения. Суммарный коэффициент в одном числе обобщает информацию, содержащуюся в коэффициентах, при этом не завися от возрастной структуры.
Суммарные коэффициенты показывают, сколько в среднем событий приходится на одного члена когорты за все время ее существования. Например, суммарный коэффициент первых браков показывает, сколько в среднем первых браков пришлось на одного члена реальной когорты или сколько в среднем первых браков пришлось на одного члена условной когорты при условии сохранения повозрастных показателей брачности, существовавших в данном календарном году, на протяжении всего срока жизни данной условной когорты. Суммарные коэффициенты рассчитываются как сумма повозрастных коэффициентов с учетом длины возрастного интервала. (Подробнее о расчете суммарных коэффициентов см. в следующих главах).
Ограничимся здесь только одним замечанием. Расчет и использование суммарных коэффициентов может таить в себе и определенные ловушки. Поскольку суммарные коэффициенты можно рассчитывать как для условного поколения (показатели итоговой рождаемости или итоговой брачности поколения) так и для условного поколения, то, например, возникает иллюзия того, что суммарный коэффициент рождаемости календарного периода можно интерпретировать как показатель интенсивности процесса рождаемости в реальных поколениях, не упоминая о его подверженности конъюнктурным колебаниям.
Нельзя считать, что уровень демографического процесса, рассчитанный на основе условного поколения, идентичен реальной интенсивности демографического процесса, поскольку условное поколение состоит из частиц реальных поколений, и интенсивность демографического процесса в усло-вном поколении зависит от повозрастных интенсивностей этого процесса в реальных поколениях. Например, значения суммарного коэффициента рождаемости могут заметно колебаться от года к году, а показатель исчерпанной рождаемости в реальных поколениях при этом практически не будет меняться (см. рис. 6.6).
120
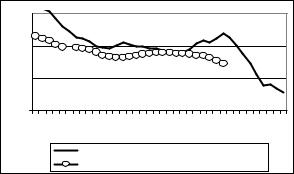
Подобная ситуация может возникнуть при изменении календаря демографических событий в реаль– ных когортах. Например, меры помощи семьям с детьми, принятые всередине 1980 гг., привели к росту суммарного коэф-
фициента |
рож- |
|
даемости |
в связи |
|
с тем, |
что |
многие |
женщины |
из раз– |
|
ных |
поколений |
|
родили очередного
2 , 5 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 , 5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1959 |
1962 |
1965 |
1968 |
1971 |
1974 |
1977 |
1980 |
1983 |
1986 |
1989 |
1992 |
1995 |
|
|
|
суммарный коэффициент рождаемости |
|
||||||||
|
|
|
итоговая рождаемость поколений |
|
|
|||||||
Рис. 6.6 Динамика суммарного коэффициента |
||||||||||||
рождаемости и показателя итоговой рождаемости |
||||||||||||
в реальных поколениях населения России |
|
|||||||||||
Источник: рисунок построен на основе следующих данных: Население России за 100 лет (1897–1997). М.: Госкомстат, 1998. Население России. 1997. Пятый ежегодный демографический доклад // Отв. Ред. А.Г. Вишневский. М., 1998.
С. 142–143.
ребенка именно в эти годы. При этом изменился только календарь рождений в когортах. Средний возраст матерей при рождении детей снизился, так как некоторое число рождений, запланированных на более поздние годы, было стимулировано принятыми мерами. Итоговая рождаемость могла и не измениться, так как женщины родили не «дополнительного», а «запланированного» ребенка, который при других условиях появился бы позже.
Этот пример наглядно показывает, что необходимо осторожно толковать показатели, полученные методом поперечного анализа, так как они испытывают влияние особых событий календарного периода.
6.5.2. Характеристика календаря демографического процесса
Время в когорте отсчитывается от момента наступления исходного события. Например, в поколении время отсчитывается от момента рождения индивидов и выражается возрастом; в брачной когорте время отсчитывается от момента регистрации брака и выражается в длительности брака. Все события в когорте можно распределить между исходным событием (время = 0) и моментом исчезновения последнего члена когорты (время w). Эти моменты (0 и w) будут верхней и нижней границами интервала, в течение которого наблюдается изучаемый процесс. Например, при изучении смертности в поколении нижняя граница соответствует моменту рождения (возраст = 0), верхняя — предельному возрасту, после которого не остается в живых ни одного члена данного поколения, например, 115 лет. Если изу-
121

чается рождаемость, то границами интервала будут нижняя и верхняя границы репродуктивного периода, то есть соответственно 15 и 49 лет.
Календарь демографического процесса характеризует распределе-
ние демографических событий в зависимости от времени, истекшего с момента формирования данной когорты. Например, распределение рождений по возрасту матери, распределение разводов по длительности брака и др. Календарь процесса можно измерить с помощью среднего интервала времени между событиями. В общем виде формула среднего интервала между событиями выглядит следующим образом1:
|
β |
|
|
|
∑i yi |
|
|
i = |
α |
, |
|
β |
|||
|
|
||
|
∑yi |
|
|
|
α |
|
где i — средний интервал между событиями; i — интервал времени между исходным событием и событием yi .
Если, например, речь идет о рождаемости, то измеряют средний воз-
раст матери при рождении ребенка:
|
49 |
τ |
|
|
|
|
∑(x + |
) n |
f x |
||
|
2 |
||||
x = |
15 |
|
|
, |
|
|
|
|
|||
49 |
|
|
|
||
|
|
|
|
|
|
|
∑ n f x |
|
|
||
|
15 |
|
|
|
|
где x — средний возраст матери при рождении ребенка; х — начало возрастного интервала, в котором наступило рождение ребенка; τ — длина возрастного интервала, в котором наступило рождение ребенка; n f x —
повозрастной показатель интенсивности рождений у женщин в возрасте x (повозрастной коэффициент рождаемости, число детей, родившихся у женщин данного возраста и др.)
Точно так же измеряется средний возраст смерти, средний возраст вступлениявбрак, характеристики календаря прочих демографических процессов.
1 Как правило, предполагается, что в интервале времени события распределены равномерно, то есть на 1/2 интервала приходится ровно половина всех событий, на 1/4 — четвертая часть ит.д. Это допущение можно использовать почти всегда, за исключением ранних детских и поздних пожилых возрастов при изучении смертности. Также необходимо помнить, что по мере увеличения интервала допускать равномерность распределения событий в интервале нужно с большой осторожностью.
122
