2. Лабораторная работа № 2 Анализ оптимального решения задачи использования ограниченных ресурсов

2.1. Краткие сведения из линейного программирования

Напомним некоторые моменты решения задачи линейного программирования (ЛП) симплексным методом.

Как известно, задача ЛП заключается в нахождении совокупности переменных x₁, x₂, … , x_n, удовлетворяющих системе линейных ограничений:

, (i= ); (2.1)

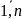(j= ), (2.2)

для которых целевая функция

Z = (2.3)

достигает максимума.

В такой постановке задача ЛП называется стандартной. Если знак неравенства в системе ограничений заменить на знак равенства, то задача ЛП примет вид основной задачи ЛП.

Переход от стандартной задачи ЛП к основной осуществляется добавлением в левую часть каждого неравенства балансовой переменной.

Как известно, для каждой задачи ЛП можно составить двойственную задачу. Сформулируем двойственную задачу для стандартной задачи ЛП, записанную в виде (2.1 – 2.3).

Алгоритм составления двойственной задачи в этом случае следующий.

1. Число переменных двойственной задачи равно числу ограничений исходной задачи и наоборот.

2. Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи и наоборот.

3. Если исходная задача решается на максимум, то двойственная – на минимум и наоборот.

4. Столбцы коэффициентов при переменных в ограничениях исходной задачи становятся строками коэффициентов при переменных в ограничениях двойственной задачи и наоборот.

5. Знаки неравенств в ограничениях исходной и двойственной задачах противоположны.

6. Условия не отрицательности для переменных двойственной задачи сохраняются.

Следуя этим правилам, составим двойственную задачу к задаче (2.1 –2.3).

Переменные двойственной задачи будем обозначать у_i (i= ). Тогда двойственная задача примет следующий вид.

Найти совокупности переменных y₁, y₂, … , y_m, удовлетворяющих системе линейных ограничений:

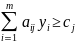, (j= ); (2.4)

(i= ), (2.5)

для которых целевая функция

W = 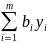(2.6)

достигает минимума.

Зная решение исходной задачи, можно найти решение двойственной задачи, не решая её. Известно, что оценки балансовых переменных в оптимальном плане исходной задачи равны оптимальным значениям переменных двойственной задачи.

Сформулируем основные теоремы ЛП, необходимые для дальнейшего.

Ограничения (2.1) и (2.5), а также (2.2) и (2.4) будем называть сопряжёнными.

Теорема 1. Для оптимальных решений прямой и двойственной задач значения целевых функций совпадают, т.е.

= (2.7)

где звёздочка означает, что значения переменных при подсчёте целевых функций берутся из оптимальных решений прямой и двойственной задач.

Теорема 2. Для каждой пары сопряжённых условий в оптимальном решении выполняются следующие соотношения; если одно из них выполняется как строгое равенство, то другое – как строгое неравенство и наоборот, т.е.

если , то , (2.8)

если , то , (2.9)

если то 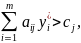(2.10)

если то (2.11)