1.2. Расчёт равновесного выпуска и равновесных цен

Решим уравнение (1.6а) относительно Х, определив равновесный валовый выпуск отраслей, обеспечивающий заданный уровень спроса Y на конечную продукцию:

X = (E – A)^-1 Y. (1.7)

Матрица

В = (Е – А) ^–1 (1.8)

называется обратной матрицей Леонтьева или матричным мультипликатором, (мультипликатором Леонтьева). Её элементы b_ij показывают потребность в валовом выпуске продукции i-й отрасли для производства единицы конечной продукции j-й отрасли и называются коэффициентами полных материальных затрат. Таким образом, В – это мультипликатор, показывающий эффект распространения спроса на валовую продукцию, первоначальным источником которого является спрос на конечную продукцию. Перепишем (1,7) с учётом (1,8) в виде

X =B Y. (1.9)

Эффект матричного мультипликатора рассчитывается из соотношения X = B Y и отражает процесс распространения спроса на валовую продукцию X, вызванный изменением спроса на конечную продукцию в объёме Y.

Говорят, что решение системы уравнений МОБ позволяет определить равновесный выпуск, имея в виду под общим равновесием соотношение в экономической системе, которое характеризуется равновесием спроса и предложения всех её элементов.

Определим равновесные цены, воспользовавшись системой уравнений производства продукции. Равновесные цены позволяют исследовать эффект распространения изменения цены, вызванный изменением элементов добавленной стоимости и построить ценовую модель МОБ.

Обозначим через v_j = z_j / x_j величину добавленной стоимости, приходящейся на единицу валовой продукции отрасли и называемой долей добавленной стоимости. Тогда, учитывая, что z_j = v_j x_j, (1.2) перепишем в виде:

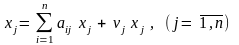(1.10)

или (1.11)

Это выражение описывает формирование цен каждого вида продукции в базовом периоде, если их принять за единицу. Слагаемое показывает возмещение стоимости, а v_j – вновь созданную стоимость (с учётом амортизации и налогов). Система равенств (1.11) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.

Если для расчётного периода доля добавленной стоимости будет равна v_j, то цены P_j (j = ) будут определяться по (1.11) из соотношений

. (1.12)

В матричном виде эту систему можно переписать как

Р = А^т Р + V. (1.13)

Матрица А^т – транспортированная матрица А.

Решим (1.13) относительно Р. Получим

P = B^T V. (1.14)

Уравнения (1.12) и (1.13) называют моделью равновесных цен, а матрицу В^т – ценовым матричным мультипликатором.

Эффект распространения Р , вызванный изменением доли добавленной стоимости на V может быть рассчитан из (1.14):

P = B^T V.