Розділ УІ. Письмове множення і ділення на двоцифрове та трицифрове число

Метою розділу є формування в учнів навичок письмового множення та ділення багатоцифрового числа на двоцифрове, ознайомлення з письмовим множенням та діленням на трицифрове число. Слід зазначити, що з письмовим прийомом множення та ділення на двоцифрове число учні вже ознайомились на початку навчального року, працюючи з числами в межах 1000. До даного часу учні вже засвоїли відповідні алгоритми і набули навички письмового множення та ділення на двоцифрове число в концентрі «Тисяча». Таким чином, створено певне підґрунтя для перенесення способу дії при письмовому множенні та діленні на двоцифрове число на випадки обчислень з багатоцифровими числами. За допомогою навчальних завдань учні переконуються в тому, що письмове множення та ділення багатоцифрового числа на двоцифрове виконується так само, як і трицифрового на двоцифрове. Учні виконують не лише письмове множення та ділення, а й перевіряють правильність одержаних результатів. Слід зазначити, що у цей час вправи в усних обчисленнях не припиняються, й учні вдосконалюють навички усних обчислень з круглими багатоцифровими числами.

У межах розділу учні продовжують учитись розв’язувати задачі. Вони знайомляться із задачами на рух, порядок розгляду яких відмінний від традиційного. Задачі на рух назустріч та рух у протилежних напрямках вводяться одночасно, але спочатку учні вчаться розв’язувати задачі на знаходження подоланого шляху, потім – на знаходження швидкості одного з тіл, після цього узагальнюється перший спосіб розв’язування задач на рух, далі – відбувається ознайомлення із другим способом їх розв’язування, і лише після засвоєння цього матеріалу учні вчаться розв’язувати задачі на знаходження часу руху. На заключному етапі задачі на рух зіставляються із задачами на спільну роботу, визначається спільне та відмінне у математичних структурах та способах розв’язування, узагальнюється математична структура задач на процеси та способи їх розв’язування. Крім роботи над задачами на рух, яка реалізує мету формування в учнів міцного вміння у їх розв’язуванні, з метою безперервного повторення вивченого учням пропонуються задачі інших видів та типів. Особливу увагу приділено задачам, що містять знаходження частини від числа та числа за величиною його частини, оскільки наступною темою передбачено вивчення дробів.

Продовжується робота над рівняннями, нерівностями зі змінною, учні знаходять значення виразів зі змінною; розв’язують задачі геометричного змісту.

Завершується розділ арифметичними діями множення та ділення іменованих чисел, які вимагають застосування письмового прийому множення на одноцифрове число, а учням з високим рівнем пізнавальних потреб і можливостей можна запропонувати й ті випадки, які передбачають ділення та множення на двоцифрове число. Окремо розглядається ділення з остачею.

Урок № 84/21 ( с. 36-37 )

Мета: формувати навички письмового множення

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати спосіб подання круглого числа у вигляді добутку числа та розрядної одиниці; спосіб послідовного множення при множенні на кругле число. Мотивувати доцільність введення письмового прийому множення трицифрового числа на кругле число. Перенести спосіб міркування при множенні двоцифрового числа на кругле на випадки множення на кругле число у межах багатоцифрових чисел. Дослідити залежність кількості нулів у добутку від кількості нулів у другому множнику при множенні на кругле число; від кількості нулів в обох множниках при множенні круглих чисел. Формувати обчислювальні навички письмового множення круглих чисел в межах багатоцифрових чисел. Актуалізувати спосіб міркування при письмовому діленні круглого трицифрового числа на кругле число, перенести спосіб міркування на випадки ділення круглих багатоцифрових чисел на кругле число, формувати обчислювальні навички ділення на кругле число в межах багатоцифрових чисел. Вдосконалювати уміння розв’язувати складені задачі, що містять знаходження частини від числа; задачі на пропорційне ділення. Вдосконалення уміння розв’язувати рівняння.

Розвивальна задача: розвивати логічне мислення учнів під час перенесення способу міркування при письмовому діленні на кругле число на випадки ділення багатоцифрового числа на кругле число.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Ми вже певний час працюємо з багатоцифровими числами. Ми навчилися виконувати і арифметичні дії додавання та віднімання з такими числами, виконувати письмове множення та ділення багатоцифрового числа на одноцифрове. Але ж досвід роботи у концентрі «Тисяча» вам підказує, що на цьому не варто зупинятися. Згадайте, чому ми навчалися після опанування письмових прийомів множення та ділення трицифрових чисел на одноцифрові? Письмовому множенню та діленню на круглі числа. (Для нагадування можна продемонструвати с. 48-49 І частини підручника.) Отже, сьогодні на уроці ми використаємо вже відомі нам способи дії у випадках множення та ділення багатоцифрових чисел на круглі, а також відкриємо спосіб множення у випадку, коли обидва множники закінчуються нулями.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

2. Усне опитування.

Див. усне опитування до уроку №2.

3. Актуалізація прийому письмового множення та ділення на кругле число в межах трицифрових чисел.

Троє учнів біля дошки одержують індивідуальне завдання з подальшою колективною перевіркою розв’язків.

Обчислити значення виразів із застосуванням письмового прийому та перевірити одержаний результат.

720 : 40 28 * 30 470 * 2

Пояснення відбуваються за пам’ятками, поданим на с. 49 підручника, частина І.

4. Актуалізація прийому послідовного множення та послідовного ділення.

Двоє учнів біля дошки одержують індивідуальне завдання.

Зіставити вирази. З’ясувати, у чому відмінність. Обчислити значення виразів, використовуючи усний прийом послідовного множення (ділення). Зробити висновок, як визначена відмінність впливає на розв’язання.

1. 56 * 30 ; 56 * 300; 560 * 300.

2. 840 : 60; 8400 : 60; 8400 : 600.

5. Актуалізація способу подання круглого числа у вигляді добутку числа та розрядної одиниці.

Завдання № 2 виконується колективно.

Які розрядні одиниці ви знаєте? Скількома нулями закінчується десять, сто, тисяча, десять тисяч? Як помножити число на розрядну одиницю? Назвіть розрядні числа – десятки (сотні, тисячі, десятки тисяч…); скількома нулями вони закінчуються? Як їх можна подати у вигляді добутку числа та розрядної одиниці?

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Мотивація введення письмового прийому множення трицифрового числа на кругле число.

Завдання № 3 виконується колективно.

Треба звернути увагу учнів, що п’ятикласниця Марина використала такий самий спосіб міркування, що й при множенні двоцифрового числа на кругле із використанням письмового прийому (його учні повторили під час індивідуального опитування); отже, при множенні трицифрового числа на кругле можна міркувати так само, як і при множенні двоцифрового числа на кругле (див. пам’ятку на с. 49 підручника ч.1).

2. Перенесення відомого способу міркування при множенні на кругле число на випадки множення круглих чисел у межах багатоцифрових чисел.

Завдання №4 виконується колективно.

У перших трьох записах стовпчиків лише другий множник містить нулі –один, два або три нулі, тому у значенні добутку треба буде приписати відповідну кількість нулів. В останньому стовпчику, на відміну від попередніх, обидва множники містять нулі, тому можна припустити, що у результаті треба буде дописати стільки нулів, скільки в обох множниках разом. Щоб продемонструвати учнями необхідність дописування кількості нулів, яка дорівнює сумі нулів наприкінці множників, можна вдатися до розгляду усного прийому:

4560 * 700 = (456 * 10) * ( 7 * 100) = (456 * 7) * ( 10 * 100) = 3192 *1000 = 3192000

Перший множник подаємо у вигляді добутку числа 456 та розрядної одиниці 10. Другий множник – у вигляді добутку числа 7 та розрядної одиниці 100. Числа можна множити у будь-якому порядку: перемножуємо числа, перемножуємо розрядні одиниці; перемножуємо одержані результати (щоб помножити число на 1000, достатньо до цього числа справа приписати три нулі). Щоб прочитати це число, розбиваємо число на класи, відраховуючи справа наліво по три розряди в кожному класі: 3 мільйони 192 тисячі.

Узагальнюємо міркування при множенні на круглі числа, читаємо пам’ятку, подану на с. 36 підручника.

3. Первинне закріплення.

Завдання № 5 виконується з коментарем.

4. Перенесення відомого способу міркування при письмовому діленні на кругле число на випадки ділення багатоцифрових чисел.

Завдання №6 виконується колективно (зразок розв’язування).

Пояснення відбувається за пам’яткою, поданою на с. 49 підручника (частина 1).

Після того, як учні пояснили подане у підручнику розв’язання, можна запропонувати з’ясувати, що змінилося у наступних частках та як ця зміна вплине на спосіб розв’язування: 1980 : 20; 2180 : 20 – все одного спосіб розв’язування лишиться тим самим – треба буде дільник подавати у вигляді добутку числа та розрядної одиниці, і добираючи цифру частки, спочатку ділити неповне ділене на розрядну одиницю, а потім – на число.

5. Первинне закріплення.

Завдання №6 (стовпчик виразів, поданий справа від готового розв’язання) виконується з коментарем.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння виконувати письмове множення круглих чисел та ділення на кругле число.

Завдання № 9 виконується учнями самостійно.

2. Вдосконалення обчислювальних навичок письмового ділення на двоцифрове число.

Для виконання біля дошки пропонуємо завдання:

Знайти значення виразів та перевірити результати:

27 * 34 754 : 26 864 : 48 19 * 47

3. Вдосконалення уміння розв’язувати задачі на пропорційне ділення.

Завдання № 8 виконується учнями самостійно.

4. Вдосконалення вміння розв’язувати складені задачі, що містять знаходження дробу від числа.

Завдання №1 із робочого зошита.

5. Вдосконалення вміння розв’язувати рівняння.

Завдання №2 із робочого зошита виконується учнями самостійно.

6. Розвиток логічного мислення учнів.

Учням з високим рівнем пізнавальних потреб і можливостей пропонуємо задачу:

Електричний настінний годинник зі стрілками відстає кожну добу на 6 хвилин. Господар поставив їх на правильний час й поїхав у відрядження. Коли він повернувся, годинник знов показував вірний час. Скільки діб він був у відрядженні?

Розв’язання. Циферблат годинника розділений на 12 частин,12 годин. Відстаючи кожну добу на 6 хвилин, годинник буде показувати точний час, коли відстануть на 12 годин, тобто через 12 год : 6 хв = ( 12 х 60 ) хв : 6 хв = 120 – стільки повних обертів повинна зробити годинна стрілка, тому пройшло 60 діб. Відповідь: господар був відсутній 60 діб або кілька разів по 60 діб.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання № 7 – записати задачу коротко схематично, за потреби виконати схематичний рисунок та розв’язати задачу, записавши розв’язання задачі по діях з поясненнями до кожної. Завдання №9 – знайти значення добутків та часток, застосувавши письмовий прийом.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Що було на уроці новим? Який ваш досвід допоміг розібратися у нових випадках обчислень? Здогадайтесь, коли вам у нагоді будуть одержані знання і вміння. Що в роботі видалося легким і зрозумілим; що викликало труднощі?

Урок № 85/22 ( с. 38-39 )

Мета: формувати навички письмового множення

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати прийом письмового множення двоцифрового числа на двоцифрове, перенести спосіб міркування на випадки письмового множення багатоцифрового числа на двоцифрове. Здійснити первинне закріплення письмового множення багатоцифрового числа на двоцифрове. Формувати навички письмового множення багатоцифрового числа на двоцифрове, прогнозування кількості цифр у значенні добутку. Узагальнити спосіб міркування при письмовому множенні на двоцифрове число, розкрити спосіб одержання неповних добутків та добутку. Дослідити відмінності у способі міркування при письмовому множенні на двоцифрове та трицифрове число, ознайомити з письмовим множенням на трицифрове число. Здійснити первинне закріплення письмового множення на трицифрове число. Зіставити випадки письмового множення на двоцифрове число з відповідним випадком письмового множення на трицифрове число, дослідити вплив відмінності на розв’язування; формувати вміння прогнозувати кількість цифр у добутку. Вдосконалювати вміння знаходити значення виразів на кілька дій; розв’язувати задачі, що містять знаходження частини від числа та числа за величиною його частини.

Розвивальна задача: розвивати логічне мислення учнів під час перенесення способу міркування в нову ситуацію; під час дослідження впливу відмінності добутків на розв’язування.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

На попередньому уроці ми навчилися виконувати множення круглих і багатоцифрових чисел. Між тим, випадки письмового множення не обмежуються лише множенням на кругле число. Які ще алгоритми письмового множення вам відомі? Ви вмієте виконувати письмове множення двоцифрового числа на двоцифрове, але ж чому обмежувати себе вимагаючи, щоб перший множник був лише двоцифровим числом… Можна множити на двоцифрове число і трицифрове, і чотирицифрове. Сьогодні на уроці ми використаємо відомий шлях міркування при множенні на двоцифрове число на випадки обчислення в межах багатоцифрових чисел. Крім того, дослідимо залежність кількості неповних добутків при письмовому множенні від кількості цифр у другому множнику, відкриємо спосіб міркування при письмовому множенні на трицифрове число. Одержані на уроці вміння допоможуть вам успішно виконувати обчислення не лише в 4-му класі, а й у 5-му, 6-му…

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

2. Математичний диктант.

1. Запишіть числа: 134256, 20560, 9007. В кожному числі підкресліть десятки однією рискою, сотні - двома, а одиниці тисяч - трьома.

2. Замініть число 56809сумою розрядних доданків.

3. Визначте загальну кількість десятків в числі 309456.

4. Запишіть врази і знайдіть їх значення:

1. Перший доданок 56000, другий доданок 27000. Знайти значення суми.

2. Ділене 760000 , дільник 4. Знайти значення частки.

3. Зменшуване 300000, від’ємник 170000. Знайти значення різниці.

4. Перший множник 4500, другий множник 9. Знайти значення добутку.

5. Добуток чисел 23000 та 7 зменшити на 8000.

6. Суму чисел 18000 та 32000 зменшити в 25 разів.

7. Знайти ¼ від різниці чисел 100000 і 36000.

8. Знайти ціле, якщо ½ дорівнює сумі чисел 3700 і 5900.

3. Актуалізація письмового прийому множення та ділення на двоцифрове число в межах тисячі; актуалізація письмового прийому множення та ділення багатоцифрового числа на одноцифрове.

У той час, поки клас працює над математичним диктантом, учень виконує індивідуальне завдання біля дошки з подальшою перевіркою.

Обчислити значення виразів, використовуючи письмовий прийом.

23834 * 4 50078 * 7 36 * 24 42 * 23

Пояснення відповідно до алгоритму, поданому у підручнику на с. 53 (частина 1).

Пригадуємо, скільки цифр може бути в значенні добутку при множенні та діленні на одноцифрове число (див. С. 44 підручника, частина 1). Зіставляємо способи міркування при письмовому множенні на одноцифрове число та двоцифрове число; з’ясовуємо, що кількість неповних добутків залежить від кількості цифр, якими записується другий множник.

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Перенесення відомого способу дії при письмовому множенні на двоцифрове число на випадки обчислень в концентрі «Багатоцифрові числа».

Завдання № 1 із робочого зошита виконується з коментарем.

Учні коментують розв’язування у першому стовпчику. З’ясовують відмінність у добутках – змінюється перший множник – у другому добутку він вже містить сотні, а у третьому – тисячі. З’ясовуємо, що ця відмінність вплине лише на те, що треба буде при обчисленні неповних добутків виконати ще й множення на сотні або на сотні та тисячі. Отже, зміняться неповні добутки, але сам спосіб міркування лишається таким самим.

У результаті виконання завдання учні доходять висновку про те, що множення багатоцифрових чисел на двоцифрове число відбувається так само, як і двоцифрових чисел на двоцифрові. Учні формулюють алгоритм дії ( см. С. 53 підручника, частина1).

2. Первинне закріплення способу дії при множенні багатоцифрового числа на двоцифрове.

Завдання № 2 виконується з коментарем.

Пояснення до поданого розв’язання: множу 3 одиниці другого множника на перший множник; при множенні числа одиниць в результаті одержую число одиниць, тому ставлю точку під одиницями і результат починаю записувати з одиниць: 3 помножити на 2, буде 6, пишу 6 в результаті; 3 на 4 , буде 12 пишу в результаті; читаю – 126 одиниць – перший неповний добуток. Множу 2 десятки другого множника на перший множник; при множенні числа десятків в результаті одержую число десятків, тому ставлю під десятками точку та результаті починаю записувати з розряду десятків: 2 помножити на 2, буде 4, записую; 2 на 4 буде 8, записую; 84 десятки – другий неповний добуток. Додаю неповні добутки: 6 пишу під одиницями; додаю десятки 2 і 4, буде 6, пишу під десятками; додаю 1 і 8 сотень, буде 9, пишу під сотнями. Читаю результат: 966 – добуток.

3. Дослідження відмінності у способі дії при письмовому множенні на двоцифрове та трицифрове число.

Завдання № 5 виконується колективно.

При множенні на двоцифрове число ми одержуємо два неповні добутки. Перший (другий) неповний добуток, виражений у одиницях (десятках), оскільки одержується множенням одиниць (десятків) другого множника не перший множник. При множенні на трицифрове число одержуємо ще й третій неповний добуток, виражений у сотнях, оскільки треба ще помножити сотні другого множника на перший множник. Отже, кількість неповних добутків залежить від кількості цифр у запису другого множника. Пропонуємо учням припустити, скільки неповних добутків буде при множенні на чотирицифрове, п’ятицифрове число.

4. Первинне закріплення визначеної відмінності у способі дії при письмовому множенні на двоцифрове та трицифрове число.

Завдання № 2 із робочого зошита виконується з коментарем.

Учні виконують письмове множення на двоцифрове число з повним поясненням, попередньо прикинувши кількість цифр у значенні добутку. При множенні на трицифрове число учням вже відомі перші два неповні добутки, лишилося обчислити значення третього неповного добутку, помноживши сотні другого множника не перший множник.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння виконувати письмове множення на двоцифрове число.

Завдання № 4 ( перші два стовпчики) і №6 виконується учнями самостійно.

2. Вдосконалення уміння обчислювати значення виразів на кілька дій. Формування обчислювальних навичок.

Завдання №7 виконується учнями самостійно.

3. Вдосконалення уміння розв’язувати складені задачі, які містять знаходження частини від числа та числа за величиною його частини.

Завдання № 8 ( 1) виконується учнями самостійно.

Після розв’язання задачі пропонуємо учням зіставити задачі 1 і 2. Встановлюємо, що задача 1 – складена, тому що її не можна розв’язати, виконавши лише одну арифметичну дію, вона складається з двох простих задач. А задача 1 – проста, в ній треба знайти число за величиною його частини; на її запитання можна відповісти відразу виконавши лише одну арифметичну дію. Учні пригадують правило знаходження числа за величиною його частини.

4. Розвиток логічного мислення учнів.

Учням з високими пізнавальними потребами і можливостями пропонуємо задачу:

Група туристів складається з 6 іноземців. Вони говорять по-англійськи та по-французьки. 3 людини розмовляють лише по-англійськи, 2 людини – лише по-французьки. Скільки людей розмовляють на двох мовах: і по-англійськи і по-французьки ?

Відповідь: 1 людина говорить і по англійські і по-французькі.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №4 ( 3-й та 4-й стовпчики) – виконати множення на двоцифрове число письмово. Завдання № 7- знайти значення виразів на кілька дій, пригадавши правила порядку виконання дій у виразах з дужками та без дужок. Завдання №8 (2) – розв’язати задачу.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Чому ви навчились сьогодні на уроці? Чи є новою для вас дія письмового множення на двоцифрове число? У чому відмінність між письмовим множенням на одноцифрове та двоцифрове число; між письмовим множенням на двоцифрове та трицифрове число? Від чого залежить кількість неповних добутків при письмовому множенні? Якими успіхами ви задоволені? Над чим є необхідність ще попрацювати?

Урок №86/23 ( с. 40-41 )

Мета: формувати навички письмового ділення та множення

Дидактичні задачі. Актуалізувати спосіб укрупнення розрядних одиниць при додаванні круглих чисел та при множенні круглого числа на одноцифрове число; спосіб множення круглого числа на одноцифрове на підставі заміни круглого числа добутком числа та розрядної одиниці; вдосконалювати уміння обчислювати значення виразу зі змінною. Актуалізувати спосіб міркування при письмовому діленні трицифрового числа на одноцифрове число шляхом заміни дільника найменшим круглим числом та подання круглого числа у вигляді добутку числа та розрядної одиниці з наступним послідовним діленням діленого на розрядну одиницю, а далі й на число; спосіб перевірки пробних цифр частки. Перенести спосіб міркування при письмовому діленні трицифрового числа на двоцифрове на випадки письмового ділення багатоцифрового числа на двоцифрове. Здійснити первинне закріплення письмового ділення багатоцифрового числа на двоцифрове. Формувати навички письмового ділення багатоцифрового числа на двоцифрове, прогнозування кількості цифр у значенні частки. Перенести спосіб міркування із визначення пробної цифри частки та прикидки пробної цифри частки на випадки письмового ділення на трицифрове число. Зіставити способи міркування при письмовому діленні на двоцифрове та трицифрове число, формувати навички письмового ділення, перевірки правильності виконання дії ділення. Зіставити задачі на знаходження четвертого пропорційного і на пропорційне ділення, визначити вплив відмінності на спосіб знаходження однакової величини і на розв’язання задачі в цілому. Вдосконалювати уміння розв’язувати складені задачі, що містять знаходження дробу від числа.

Розвивальна задача: розвивати логічне мислення учнів.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

На попередньому уроці ми множили багатоцифрові числа на двоцифрові. Між тим, ми вже звикли щоразу перевіряти правильність розв’язку. Яких знань нам бракує, щоб виконати таку перевірку? Ми ще не вміємо виконувати письмове ділення багатоцифрового числа на двоцифрове. Цікаво, чи вдасться нам справитись із письмовим діленням багатоцифрового числа на двоцифрове. Чи буде цей випадок для вас зовсім новим?

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усне опитування.

Див урок №3.

2. Математичний диктант.

1. Знайти добуток чисел 56000 та 8.

2. Знайти частку чисел 9600 та 400.

3. Число 260000 збільшити в 3 рази.

4. Число 60000 зменшити в 15 разів.

5. Знайти невідомий доданок, якщо значення суми 41000, а відомий доданок 17000.

6. Знайти невідомий дільник, якщо ділене 720000 значення частки 6.

7. Знайти невідоме зменшуване, якщо значення різниці 23000, а від’ємник 18000.

8. Знайти невідомий множник, якщо значення добутку 7200, а відомий множник 300.

9. Знайти невідомий від’ємник, якщо зменшуване 310000, і значення різниці 150000.

10. Знайти невідоме ділене, якщо дільник 45, а значення частки 300.

Під час перевірки математичного диктанту, з’ясовуємо які обчислювальні прийоми можна використати при множенні, при діленні, при додаванні, при відніманні. Зазначимо, що в усіх випадках обчислення використовується прийом укрупнення розрядних одиниць, коли круглі числа замінюємо більшими розрядними одиницями і виконуємо дії з числами розрядних одиниць; при додаванні, відніманні одержуємо число в тих самих розрядних одиницях; при діленні слід бути уважним: при діленні числа більших розрядних одиниць на число без найменування одержуємо число в тих самих розрядних одиницях ( ділення на рівні частини), а при діленні круглого числа на кругле ділимо числа більших розрядних одиниць і одержуємо число без найменування (ділення на вміщення). А у випадках множення та ділення на кругле число можна ще й використати прийом послідовного множення та ділення. Звертаємо увагу учнів особливо на випадки ділення на кругле число, і записуємо розв’язання на дошці: 9600 : 400 = 9600 : ( 100 * 4 ) = (9600 : 100) : 4 = 96 : 4 = 24.

Звертаємо увагу на завдання 3) та 6) і пригадуємо скільки цифр може бути в значенні частки в разі ділення на одноцифрове число ( с. 44 підручника, частина 1).

3. Актуалізація прийомів множення круглого числа на одноцифрове.

Під час математичного диктанту кількома учнями виконується біля дошки завдання №1.

Під час колективної перевірки звертаємо увагу учнів на окремі моменти: якщо к = 7000 або к = 46000, то обчислення 30000 * 5 можна різними способами, використовуючи усні прийоми – укрупненням розрядних одиниць або на підставі правила множення добутку на число, а можна використати раціональний прийом множення на 5: 30000 * 5 = 30000 : 10 * 2 = 3000 * 2 = 6000. Якщо к = 18500, для багатьох учнів зручнішим буде письмовий прийом, хоча окремі учні можуть застосувати і усні прийоми. Між тим, в усіх випадках обчислення можна було здійснити не користуючись правилами порядку дій у виразах, що містять дужки, а на підставі правила множення суми на число (розподільного закону множення відносно додавання): щоб помножити суму на число, достатньо кожний доданок суми помножити на це число і одержані добутки додати.

4. Актуалізація прийому письмового ділення трицифрового числа на двоцифрове.

Знайти значення часток та перевірити одержані результати:

989 : 43 896 : 28 448 : 64

Розгорнені пояснення відбуваються відповідно до пам’яток на с. 60 ( пункти 2 – 4), на с. 49, на с.64 підручника, частина 1. Після виконання завдання №1 відбувається колективна перевірка. Звертаємо увагу учнів на залежність між кількістю цифр частки та кількістю неповних ділених: у частці дві цифри, тому матимемо й два неповні ділені; у значенні частки одна цифра, тому й буде лише одне неповне ділене.

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Перенесення відомого способу міркування при письмовому діленні на двоцифрове число на випадки обчислення з багатоцифровими числами.

Завдання №1 із робочого зошита виконується з коментарем. Вчитель дублює записи на дошці під диктовку учнів.

Відмінність другої частки від першої полягає в тому, що змінилося ділене, але перше неповне ділене буде таким самим, але у інших розрядних одиницях ( тому зміниться найвищий розряд значення частки та кількість цифр у значенні частки, а тому й зміниться кількість неповних ділених); зміниться друге неповне ділене й додається ще третє неповне ділене. Учні коментують розв’язування.

2. Первинне закріплення способу міркування при письмовому діленні багатоцифрового числа на двоцифрове.

Завдання № 2 виконується колективно.

1) Визначаємо перше неповне ділене: у дільнику 2 цифри, тому в діленому виокремлюємо зліва дві цифри і читаю число з назвою розрядних одиниць – 31 тисяча; 31 тисячу не можна розділити на 71, щоб одержати хоч би одну тисячу, тому переходимо до наступного розряду – 315 сотень – це перше неповне ділене. 2) Визначаємо найвищий розряд та кількість цифр у значенні частки: оскільки перше неповне ділене сотні, то й в значенні частки у найвищому розряді будуть сотні, щоб записати число з цим найвищим розрядом потрібно три цифри, тому у значенні частки будуть три цифри, ставимо три точки. 3) Ділимо перше неповне ділене на дільник, для цього дільник 71 замінюємо близьким меншим круглим числом 70, 70 – це 10 помножене на 7. 315 ділю на 10, для цього прикриваємо справа одну цифру, буде 31, 31 ділимо на 7 , можна взяти лише по 4. 4 – це пробне цифра частки, її слід перевірити. Прикидаємо: множимо 4 на десятки дільника ( 4 * 70 = 280), від неповного діленого віднімаємо одержане число ( 315 – 280 = 35) і порівнюємо остачу з добутком 4 на одиниці дільника; звичайно що 35 вистачить, щоб 4 помножити на 1, тому цифру 4 пишемо на місці сотень у значенні частки. 4) Дією множення дізнаємось, скільки сотень розділилося: 4 помножити на 1, буде 4, пишемо під цифрою 5; 4 помножити на 7 , буде 28, підписуємо під цифрами 1 та 3 відповідно. 5) Дією віднімання дізнаємось, скільки сотень не розділилось - від 315 віднімаємо 284: п’ять мінус чотири, буде 1; від 1 не можна відняти 8, позичаємо одиницю вищого розряду, маємо 11 відняти 8, буде 3; було 3, позичили 1, залишилось 2; від 2 відняти 2 буде 0, нуль під рискою не пишемо; 31 сотня не розділилася. 6) Порівнюємо остачу з дільником: остача 31 менша за дільник 71, тому цифру частки дібрано правильно. Або: 31 сотню не можна розділити на 71, щоб одержати хоч би одну сотню, тому цифру сотень дібрано правило. 7) Утворюємо друге неповне ділене: остачу 31 сотню перекладаємо у десятки: 310 десятків та ще 9 десятків діленого, маємо 319 десятків – друге неповне ділене. 8) Ділимо друге неповне ділене на дільник, для цього дільник 71 замінюємо близьким круглим числом 70, 70 – це 10 помножене на 7. 319 ділю на 10, для цього прикриваємо справа одну цифру, буде 31, 31 ділю на 7 , можна взяти лише по 4. 4 – це пробне цифра частки, її слід перевірити. Прикидаємо: множимо 4 на десятки дільника ( 4 * 70 = 280), від неповного діленого віднімаємо одержане число ( 319 – 280 = 39) і порівнюємо остачу з добутком 4 на одиниці дільника; звичайно що 39 вистачить, щоб 4 помножити на 1, тому цифру 4 пишемо на місці сотень у значенні частки. 4) Дією множення дізнаймось, скільки сотень розділилося: 4 помножити на 1, буде 4, пишемо під цифрою 5; 4 помножити на 7 , буде 28, підписуємо під цифрами 1 та 3 відповідно. 5) Дією віднімання дізнаємось, скільки сотень не розділилось - від 319 віднімаємо 284…; 35 десятків не розділилася. 6) Порівнюємо остачу з дільником: остача 35 менша за дільник 71, тому цифру частки дібрано правильно. Або: 35 десятків не можна розділити на 71, щоб одержати хоч би один десяток, тому цифру десятків дібрано правило. 7) Утворюємо третє неповне ділене: остачу 35 десятків перекладаємо в одиниці: 350 десятків та ще 5 одиниць діленого, маємо 355 десятків – третє неповне ділене…

3. Дослідження відмінності у способі міркування при письмовому діленні на двоцифрове та трицифрове число.

Завдання № 4 виконується колективно.

Спільне: при діленні на двоцифрове та трицифрове число дільник замінюємо блискотим меншим розрядним числом, яке потім подаємо у вигляді добутку розрядної одиниці та числа; ділимо неповне ділено спочатку на розрядну одиницю ( прикриваємо у числі справа стільки цифр, скільки нулів у розрядній одиниці), а потім одержаний результат ділимо на число… Відмінність полягає лише в тому, що при визначенні першого неповного діленого при діленні на двоцифрове число ми ліворуч у діленому спочатку відділяємо дві цифри, а при діленні на трицифрове число – три цифри; при діленні неповного діленого на дільник замінивши дільник близьким меншим круглим числом у випадку ділення на двоцифрове число ми неповне ділене ділимо спочатку на 10, а потім на число; а при діленні на трицифрове число – ділимо спочатку на 100, а потім на число. Всі інші кроки міркування при письмовому діленні на двоцифрове та трицифрове число ті й самі.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння виконувати письмове ділення на двоцифрове число.

Завдання № 3 виконується колективно, а 2-й стовпчик - з коментарем.

Завдання № 5 виконується з коментарем.

Робота за сходинками складності: І сходинка – виконати письмове ділення на двоцифрове число з перевіркою; ІІ сходинка – виконати письмове ділення на трицифрове число з перевіркою.

2. Вдосконалення уміння розв’язувати задачі на знаходження четвертого пропорційного та на пропорційне ділення.

Завдання №6 (1) виконується учнями самостійно.

Після перевірки розв’язання задачі, учні читають задачу 2 якщо короткий запис задачі 1 виконаний на дошці, то вносимо зміни у короткий запис, і з’ясовуємо спільне: у задачі 2 ті самі взаємопов’язані величини, два випадки, маса 1 торбини однакова для обох випадків, для кількості торбин дано два числові значення; шуканим є значення загальної величини. Відмінність: у задачі 1 – одне шукане, а в задачі 2 – шуканими є два значення загальної величини, але дано їх суму. Задача 2 – це задача на пропорційне ділення. Ключем до її розв’язання так само є значення однакової величини, але однакову величину можна знайти за двома сумами. Вчитель повідомляє учням, що розв’язувати задачу 2 вони будуть вдома.

3. Вдосконалення вміння розв’язувати складені задачі, що містять знаходження частини від числа.

Завдання №2 із робочого зошита виконується учнями самостійно.

Робота за сходинками складності: І – розв’язати задачу; ІІ – скласти і розв’язати обернену задачу, так, щоб шуканим було число 429.

4. Розвиток логічного мислення учнів.

Завдання № 7 пропонуємо учням з високими пізнавальними потребами і можливостями.

1. Розпилів на 1 менше, ніж оцупків, тому оцупків на 1 більше ніж розпилів: 9 + 1 = 10 оцупків. Отже 6м колоду розпиляли на 10 рівних частин, тому довжина однієї частини: 600 см : 10 = 60 см.

2. Дізнаємось, скільки всього одержали оцупків: 6 м : 1 м = 6 оцупків. Оцупків на 1 більше, ніж розпилів, тому розпилів на 1 менше, ніж оцупків: 6 – 1 = 5 розпилів.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання № 5 виконати письмове ділення на двоцифрове число з перевіркою. Завдання №6 (2) – розв’язати задачу, записавши її коротко в формі таблиці.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Чому ви сьогодні вчилися на уроці? Чи можна міркувати при письмовому діленні багатоцифрового числа на двоцифрове так само, як при письмовому діленні трицифрового числа на двоцифрове? Чим відрізняються ці випадки письмового ділення? Від чого залежить кількість неповних ділених? Скільки цифр може бути у значенні частки у разі ділення на одноцифрове число? на двоцифрове число? на трицифрове число? Що в роботі видалося складним? Якими досягненнями ви задоволені?

Урок № 87/24 ( с. 42-43 )

Мета: формувати навички письмового ділення та множення

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати усний прийом укрупнення розрядних одиниць при множенні та діленні круглого числа на одноцифрове число; спосіб множення на підставі правила множення добутку на число ( сполучного закону множення), ділення на підставі правила ділення добутку на число. Актуалізувати письмовий прийом ділення трицифрового числа на одноцифрове та двоцифрове число, ділення багатоцифрового числа на двоцифрове; перенести спосіб міркування на випадки ділення багатоцифрових чисел, що закінчуються нулями. Формувати навички письмового ділення багатоцифрового числа на двоцифрове число; перевірки ділення множенням; навички письмового множення на двоцифрове число. Актуалізувати розуміння фізичного змісту швидкості як шляху, що долає тіло за одиницю часу. Вдосконалювати вміння розв’язувати задачі на знаходження четвертого пропорційного, що містять величини швидкість час, шлях, двома способами: способом відношень і способом знаходження однакової величини; уміння розв’язувати обернені задачі на різницеве порівняння двох часток з величинами швидкість, час, шлях. Організувати спостереження за одночасним рухом двох тіл назустріч та у протилежних напрямках; зумовити висновки про зміну відстані між тілами, про складові всієї відстані, про час спільного руху.

Розвивальна задача: розвивати логічне мислення під час зіставлення випадків ділення та перенесення способу міркування в нову ситуацію.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Сьогодні на уроці ми продовжимо тренування свого мозку. Вчені вважають, що заняття математикою є найкращим тренажером. Ми продовжимо опановувати письмові прийоми множення та ділення багатоцифрових чисел на двоцифрове число. Іноді від дорослих можна почути, що для обчислень достатньо мати калькулятор, який сам справиться з будь-яким випадком множення чи ділення. Спробуйте спростувати таку думку. Інша частина уроку буде присвячена задачам з величинами: швидкість руху, час руху, подоланий шлях. Чи корисними для життя є такі задачі? Зверніть увагу – яка цінна для життя математика!

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 із робочого зошита виконується учнями самостійно.

2. Усне опитування.

Питання конструюються за матеріалами форзаців підручника ( частина 1). Додатково: правило множення числа на добуток, правило ділення добутку на число. Щоб помножити (розділити) добуток на число, достатньо один із множників помножити (розділити) на це число і одержаний результат помножити на інший множник.

3. Актуалізація усних прийомів обчислення при множенні та діленні круглих чисел.

Завдання №1 виконується колективно.

Зразки пояснень див. урок №5, завдання №3,4.

4. Актуалізація письмового прийому ділення на двоцифрове число. Перенесення письмового прийому на випадки письмового ділення круглих багатоцифрових чисел.

Завдання № 2 виконується колективно.

Три учні біля дошки виконують письмове ділення (перший рядок). Після коментування знаходження значення першої частки учитель звертає увагу учнів на наступні частки у стовпчику; учні помічають, що вони відрізняються лише діленими – у наступних ділених є один або кілька нулів. З’ясовуємо, що подане на дошці розв’язання допоможе знайти значення наступних часток: в другому рядку – одержане число характеризує число десятків значення частки, тому що в цьому випадку ще треба розділити одиниці діленого на дільник: 0 одиниць поділити на 9, буде 0 нуль, пишемо нуль у розряді одиниць у значенні частки; у третьому випадку ділене закінчується вже двома нулями, тому одержаний у першому виразі результат – це число сотень значення частки, оскільки треба ще виконати ділення двох неповних ділених на дільник: ІІІ-го – 0 десятків та ІУ – 0 одиниць. Можна було міркувати і інакше: зіставивши ділені у першому стовпчику з’ясовуємо, що одне з них містить 513, але в першому виразі – це 513 одиниць, тому в результаті одержимо число одиниць; у другому – число десятків, тому у результаті одержимо число десятків, щоб його перетворити у одиниці, треба дописати справа до нього один нуль; у третьому – це число сотень, тому до нього справа требу приписати два нулі. Аналогічно працюємо над рештою стовпчиків.

5. Актуалізація фізичного змісту швидкості.

Завдання № 4, 5 виконується колективно.

Пояснення дививсь до завдання №2,3 ( с. 114-115 підручника, частина 1) , урок №55.

6. Актуалізація уміння розв’язувати складені задачі з величинами швидкість руху, час руху, подоланий шлях.

Завдання № 1 (1) виконується колективно.

Перед розв’язанням задачі пригадуємо правила та відповідні формули знаходження швидкості та часу руху, подоланого шляху ( див. с. 114, 116 підручника, частина 1.)

Про що розповідається в задачі? (Про рух літака.) Які величини описують процес руху? (Швидкість руху, час руху, подоланий шлях.) Запишіть задачу коротко в формі таблиці. Що означає число 3? Число 2700? Число 6? Яке число є шуканим? Що означає однакова величина? Це задача на знаходження четвертого пропорційного. Що є ключем до розв’язання задачі? Як знайти однакову величину в цій задачі? Складаємо план розв’язування задачі: 1) знаходимо швидкість руху літака, однакову величину, дією ділення; 2) знаходимо подоланий шлях в ІІ випадку, відповідаємо на запитання задачі, дією множення. Учні самостійно записують розв’язання задачі та відповідь.

Зіставляємо задачу 2 і 1. З’ясовуємо, що в задачі 2 вже швидкість руху не є однаковою величино. Ця зміна вплине на розв’язання таким чином, що додасться ще одна арифметична дія, якою ми дізнаємось про швидкість літака у ІІ випадку. Цю задачу учні будуть розв’язувати вдома.

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Ознайомлення із одночасними рухом двох тіл в різних напрямках.

Вчитель викликає до дошки двох учнів, які встають по різні сторони класу та за командою вчителя розпочнуть рухатися назустріч один одному, а зустрівшись один з одним зупиняться. Клас має спостерігати: 1) як змінюється відстань між учнями; 2) що можна сказати про час руху кожного учня; 3) з чого складається шлях, який подолали обидва учні.

Після зустрічі учні повертаються спинами один до одного і за командою вчителя розпочинають рухатись у протилежні напрямки, й за командою припиняють рух.

Учні роблять висновки ( див. текст у рамочці, на с. 43 підручника). Звертаємо увагу на те, що рух у різних напрямках може відбуватися за двома варіантами: назустріч та у протилежних напрямках. Також наголошуємо на тому, що зараз розглядаються ситуації, коли рух двох тіл розпочинається одночасно і припиняється одночасно.

2. Первинне закріплення.

Завдання № 8 виконується колективно.

Вчитель звертає увагу учнів на короткий запис у вигляді креслення. Якщо учні рухаються назустріч один одному (у протилежні напрямки), то стрілочки спрямовані відповідно; над цими стрілочками пишуть значення швидкостей тіл; місце зустрічі (місце, з якого почався рух) позначається прапорцем; над прапорцем записують час руху; відрізки, що позначають шлях кожного тіла позначаємо фігурними дужками; загальний шлях ілюструє цілий відрізок, його, так само, позначаємо фігурною дужкою.

Звертаємо увагу учнів на буквений запис сформульованих висновків.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння виконувати письмове ділення та множення на двоцифрове число.

Завдання № 3 – перший стовпчик виконується з коментарем; другий – самостійно учнями.

2. Вдосконалення вміння розв’язувати складені задачі, обернені до задач на різницеве порівняння двох часток.

Завдання №2 із робочого зошита виконується учнями самостійно.

3. Розвиток логічного мислення учнів.

За наявності резерву часу учням з високими пізнавальними потребами і можливостями пропонуємо задачу:

В класі 25 учнів. З них 6 учнів або не вміють грати в шашки, або в шахи. 18 учнів вміють грати в шашки, 20 – в шахи. Скільки учнів класу грають і в шашки і в шахи?

Розв’язання. Відомо, що 18 учнів грають в шашки, тому 25 – 18 = 7 учнів не вміють грати в шашки. Якщо ми із 7 – 6 = 1 учнів не вміють грати в шашки, але можуть вміти грати в шахи. Так як 20 учнів вміли грати в шахи, то 20 – 1= 19 учнів могли грати і в шахи і в шашки.

Відповідь: 19 учнів

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №3 – виконати письмове ділення на двоцифрове число та перевірити одержаний результат. Завдання № 7 (2) – записати задачу коротко в формі таблиці та записати розв’язання задачі по діях та виразом.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

З якими випадками письмового ділення ви працювали сьогодні на уроці? Як можна міркувати при письмовому діленні чисел, що закінчуються нулями? Що, крім цього, важливим було на уроці? Як можуть рухатися два тіла одне відносно одного? Які висновки можна зробити, спостерігаючи за одночасним рухом двох тіл назустріч одне одному? У протилежних напрямках? Коли вам доводилось спостерігати за таким рухом? Чим важливі задачі на рух? Поділіться враженнями від своєї роботи: що вдається добре; що викликає проблеми.

Урок №88/25 ( с. 44-45 )

Мета: формувати навички письмового ділення та множення

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати прийом ділення з остачею, в тому числі й у випадках ділення меншого числа на більше. Актуалізувати прийом письмового ділення багатоцифрового числа на одноцифрове у випадках, коли в середині запису частки є нуль. Зіставити способи міркування при письмовому діленні багатоцифрового числа на одноцифрове та багатоцифрового числа на двоцифрове, коли в середині запису частки є нулі; перенести спосіб міркування на випадки ділення багатоцифрового числа на одноцифрове; актуалізувати розуміння залежності значення частки від збільшення дільника. Формувати навички письмового ділення багатоцифрового числа на двоцифрове у випадках, коли в середині значення частки є нулі. Актуалізувати розуміння характеру зміни відстані між тілами під час одночасного руху двох тіл назустріч та у протилежних напрямках; числове значення зміни відстані між тілами за одиницю часу. Вдосконалювати уміння розв’язувати задачі на знаходження невідомих за двома різницями, в яких однаковим є час; перетворювати задачі на знаходження невідомих за двома різницями на задачу на знаходження четвертого пропорційного.

Розвивальна задача: розвивати функціональне мислення під час дослідження залежності значення частки від зміни дільника; логічне мислення під час перетворення задачі на знаходження невідомих за двома різницями на задачу на знаходження четвертого пропорційного.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Щоразу ми відзначаємо, що раніше вивчений матеріал є гарним помічником у засвоєнні нового. Так і сьогодні: ми продовжимо вправлятися у письмовому діленні багатоцифрового числа на двоцифрове. Розглянемо цікаві випадки, які будуть не складними, якщо пригадаєте прийом ділення з остачею, коли ділене менше за дільник. Також продовжимо розглядати ситуації, які описують одночасний рух двох тіл у різних напрямках. Цікаво, чи корисним цей матеріал буде для нових задач?

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

2. Математичний диктант.

1. Запишіть швидкість руху: хлопчика, якщо він щогодини проходить по 5 км; швидкість велосипедиста, якщо він щосекунди долає по 10 м.

2. Знайдіть швидкість машини, яка за 3 години подолала 222 км, рухаючись з однаковою швидкістю.

3. Знайдіть шлях, який подолав велосипедист за 20 хвилин, рухаючись зі швидкість 12 м/с.

4. За який час мотоцикліст подолає 150 км рухаючись зі швидкістю 75 км/ год?

5. Турист має подолати 105 км, Він подолав 1/7 всього шляху. Скільки кілометрів подолав турист?

6. Спортсмен пробіг 200 м, що становить 1/25 дистанції. Яку дистанцію має подолати спортсмен?

7. Два хлопчики вирушили одночасно назустріч один одному і зустрілись через 7 хвилин. Скільки хвилин рухався кожний хлопчик до зустрічі?

8. Подати у метрах: 35 км, 1 дм, 1 см, 1 мм.

9. Подати у хвилинах: 3 год, 1 с, 2 доби.

3. Усне опитування.

1. Що означає швидкість руху машини 60 км/год; швидкість руху велосипедиста 12 м/с; швидкість руху дівчинки 4 км/год?

2. Як знайти швидкість руху (час руху, подоланий шлях)? Якою буквою позначається ця величина? Запишіть формулу.

3. Як зміниться швидкість руху, якщо час (подоланий шлях) збільшиться в кілька разів, а подоланий шлях (час) не зміниться? Як зміниться час руху, якщо швидкість руху (подоланий шлях) зменшиться в кілька разів, а подоланий шлях (швидкість) не зміниться?

4. Як зміниться подоланий шлях, якщо швидкість (час) руху збільшиться у кілька разів, а час (швидкість) руху не зміниться?

5. Які висновки можна зробити при одночасному русу назустріч (у протилежні напрямки)?

6. Із двох міст одночасно назустріч вийшли два пішоходи і зустрілися через 3 години. Скільки часу рухався кожний пішохід? ( 3 години)

7. Із села в місто вийшов пішохід і в цей же час із міста назустріч йому виїхав мотоцикліст, який зустрів пішохода через 40 хвилин. Скільки часу рухався до зустрічі пішохід? ( 40 хвилин)

8. Два пішоходи вийшли одночасно в протилежних напрямах і закінчили свій рух через 2 години. Скільки часу рухався кожний пішохід? Що можна сказати про відстань, яку пройшов кожний пішохід, якщо:

• вони рухалися з однаковою швидкістю; ( відстань однакова, тому що швидкості однакові в обох пішоходів та час руху, теж однаковий – 2 год.);

• швидкість першого більше швидкості другого; ( відстань, яку пройшов перший пішохід, більша за відстань, яку пройшов другий; при однаковому часі руху, швидкість і відстань змінюються одному напрямі: чим більше швидкість, тим більша відстань).

4. Актуалізація способу міркування при діленні з остачею.

Завдання № 2 виконується з коментарем.

В усіх випадках не можна виконати ділення націло, можна виконати ділення з остачею. У другому та четвертому випадках ділене менше за дільник. За цією ознакою розбиваємо частки на дві групи. Пригадуємо, що при діленні меншого числа на більше у неповній частці одержуємо нуль, а ділене переходить у остачу. Виконуємо ділення в кожній групі і перевіряємо одержані результати (множимо неповну частку на дільник, додаємо остачу, і якщо одержуємо ділене, то ділення виконано правильно.)

5. Актуалізація письмового прийому ділення багатоцифрового числа на одноцифрове, у випадку, коли значення частки містить нулі в середині запису.

Завдання № 3 виконується з коментарем.

Пропонуємо учням виконати запис розв’язання розгорнено з фіксацією всіх неповних ділених, одиниць певного розряду, що розділились ( див. №3 на с.2, (запис зліва) підручника, частина 2). Наявність нуля в середині запису значення частки залежить від неповного діленого: якщо число розрядних одиниць менше за дільник, то при діленні меншого числа на більше у неповній частці одержуємо нуль. Можна міркувати інакше: число розрядних одиниць не можна розділити на дільник так, щоб одержати хоча б одну одиницю цього розряду, тому в значенні частки пишемо в цьому розряді нуль.

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Перенесення способу міркування при письмовому діленні багатоцифрового числа на одноцифрове, коли в середині запису частки є нулі, на аналогічні випадки ділення багатоцифрового числа на двоцифрове число.

Завдання № 4 виконується колективно.

2. Первинне закріплення.

Завдання №1 із робочого зошита виконується з коментарем.

19228 : 4: третє неповне ділене 2 десятки; при діленні 2 на 4 в значенні частки одержимо нуль. Пишемо нуль на місці десятків у результаті… Або: 2 десятки не можна розділити на 4, щоб одержати хоча б один десяток, тому на місці десятків у значенні частки пишемо нуль. Дією множення дізнаємось, скільки десятків розділилося: 0 * 4 = 0. Дією віднімання дізнаємось, скільки десятків не розділилося: 2 – 0 = 2.

39228 : 28: третє неповне ділене 2 десятки; при діленні 2 на 28 в значенні частки одержимо нуль. пишемо нуль на місці десятків у результаті. Або: 2 десятки не можна розділити на 28 , щоб одержати хоч би один десяток, тому на місті десятків у значенні частки пишемо нуль. Дією множення дізнаємось, скільки десятків розділилося: 0 * 28 = 0. Дією віднімання дізнаємось, скільки десятків не розділилося: 2 – 0 = 2.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння виконувати письмове ділення на двоцифрове число, коли у середині запису частки є нулі.

Завдання № 5 виконується з коментарем.

2. Закріплення висновків про зміну відстані між тілами, час руху кожного тіла та складу загального шляху при одночасному русі назустріч та у протилежні напрямки. Дослідження числового значення зміни відстані між тілами за одиницю часу.

Завдання № 6 виконується колективно.

1. До задачі 1) підходить короткий запис справа. За коротким записом пояснюємо: 70 км/год – швидкість першого автомобіля – це означає, що цей автомобіль щогодини долає по 70 км; 60 км/год – швидкість першого автомобіля – це означає, що цей автомобіль щогодини долає по 60 км. Оскільки автомобілі рухаються у протилежних напрямках, то вони відділяються один від одного: перший щогодини віддаляється від другого на 70 км, а другий – віддаляється від першого ще на 60 км; отже вони разом один від одного віддаляються на 70 + 60 = 130 (км) – відстань між автомобілями змінюється на суму шляхів, що долає кожний автомобіль за одиницю часу. Вся відстань між автомобілями на момент закінчення руху буде складатися з шляху подоланого першим автомобілем (відстань, на яку він віддалився від другого за весь час руху) і з шляху, подоланого другим автомобілем за весь час руху (відстань, на яку він віддалився від першого автомобіля за весь час руху).

2. До задачі 2) підходить короткий запис, поданий ліворуч. Аналогічно пояснюємо значення швидкостей автомобілів. Число 3 означає час руху до зустрічі, а також – час руху першого автомобіля, а також – час руху другого автомобіля. Оскільки автомобілі рухаються назустріч один одному, о відстань між ними буде зменшуватись. Оскільки перший автомобіль долає щогодини по 70 км, то він наближається до другого щогодини на 70 км. Оскільки другий автомобіль долає щогодини по 60 км, то він наближається до першого щогодини на 60 км. Отже, разом, один до одного автомобілі наближаються на (70 + 60 = 130 (км)) на суму шляхів, які вони долають за одиницю часу.

Робимо узагальнюючий висновок: при одночасному русі назустріч та у протилежні напрямки, відстань між тілами змінюється на суму шляхів, які вони долають за одиницю часу.

Навч. Зошит. Ч. 3 с.3 правило:

Для закріплення цього висновку можна запропонувати учням завдання №2 із робочого зошита виконується з коментарем.

А також:

3. Розвиток логічного мислення учнів.

За наявності резерву часу учням з високими пізнавальними потребами і можливостями можна запропонувати задачі:

Чи відомо тобі, що серед усіх порід кішок тільки гепарди не втягують кігті. Кігті, в них завжди ззовні, як у собак. Серед мешканців площадки молодняку у зоопарку 18 – котеня та щеня різних порід. З них 9 – щенят, а 13 не втягують кігті. Скільки мешканців – гепарди і скільки котенят інших порід?

Розв’язання. Серед 13 малюків, не витягують кігті, 9 –щенят, тому (13 – 9) = 4 – гепарди. Кошенят інших порід 18 – ( 9 + 4 ) = 5. Відповідь: 4 гепарди і 5 кошенят інших порід.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання № 5 – виконати ділення письмово та за бажанням перевірити одержані результати. Завдання № 7 – записати задачу коротко в формі таблиці та розв’язати задачу; за бажанням перетворити задачу на знаходження четвертого пропорційного та розв’язати її.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

З якими випадками ділення на двоцифрове число ви ознайомились сьогодні на уроці? Чому з’являється нуль в середині запису значення частки? Які задачі ви розв’язували? Які висновки можна зробити при одночасному русі назустріч ( а протилежні напрямки)? Що можна сказати про числове значення зміни відстані між тілами при русі назустріч? При русі у протилежні напрямки? Оцініть свою роботу на уроці. Що, на вашу думку, є успішним? Над чим треба додатково попрацювати?

Урок № 89/26 ( с. 46-47 )

Мета: формувати уміння розв’язувати задачі на одночасний рух двох тіл в різних напрямках; формування навички письмового множення та ділення

Дидактичні задачі. Вдосконалювати навички усних обчислень. Ознайомлювати із задачами на одночасний рух тіл назустріч на знаходження відстані між тілами на момент початку руху; змінити числові дані задачі і дослідити вплив цієї зміна на план розв’язування; змінити в умові напрямок руху для одержання задачі на одночасний рух в протилежних напрямках, і дослідження впливу цієї зміна на розв’язання задачі; зміна числових даних одержаної задачі і дослідження впливу цієї зміни на розв’язання задачі. Узагальнити спосіб розв’язування задач на знаходження відстані при одночасному русі двох тіл назустріч та у протилежних напрямках; задачі з буквеними даними; узагальнений план розв’язування задач цього типу. Формувати уміння розв’язувати задачі на знаходження відстані під час одночасного руху двох тіл в різних напрямках. Формувати навички письмового ділення та множення на двоцифрове число.

Розвивальна задача: розвивати логічне мислення учнів під час дослідження задач та узагальнення способу їх розв’язування .

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Сюжети задач, які ми розв’язуємо на уроках математики, відображують ситуації, що реально відбуваються у житті людини. Так, матуся йде до супермаркету й здійснює покупки. Задачі, в яких йдеться про процес покупки ми вже розв’язували. Батько працює на заводі, виготовляє прилади. І така задача нам траплялася. Про такі задачі кажуть: «задачі на процеси». Щодня ви спостерігаєте за процесом руху, наприклад, за спільним рухом двох тіл. Наведіть приклади. Машини їдуть назустріч по зустрічних смугах; діти, граючись, біжать у різні сторони… Подібні ситуації ми вже спостерігали і на уроці, навіть робили певні висновки, - саме вони допоможуть розв’язувати задачі на рух, з якими ознайомимось сьогодні.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 із робочого зошита виконується учнями самостійно.

2. Усне опитування.

• Пояснити зміст речень: равлик повзе зі швидкістю 6 ; літак летить зі швидкістю 950 .

• Назвіть швидкість, з якою на вашу думку їде машина: 6 , 80 , 8 .

• Чому дорівнює швидкість руху: меч-риби, якщо вона за кожну годину пропливає по 100 км; верблюда, якщо він за кожну годину проходить 25 км.

• Які висновки можна зробити, спостерігаючи одночасний рух назустріч ( у протилежні напрямки): про зміну відстані між тілами та про її числове значення, про час руху, про загальний шлях, який подолали обидва тіла.

• Як на кресленні проілюструвати одночасний рух назустріч ( у протилежних напрямках): як треба накреслити стрілочки, що слід написати над стрілочками, що означає прапорець, що пишуть поряд з прапорцем?

• Два лижники вийшли одночасно назустріч один одному. Перший лижник йшов зі швидкістю 12 , а другий – 14 . Як змінюється відстань між лижниками? (Відстань при одночасному русі назустріч весь час зменшується.)На скільки зменшиться відстань за 1-шу годину, за 2-гу годину ? За дві години? ( 12 – це означає, що перший лижник за кожну годину проходив по 12 км; 14 – означає, що другий лижник за кожну годину проходив по 14 км. Отже, за першу годину перший лижник наблизився на 12 км, а другий – на 14 км, тому всього вони наблизилися : 12 + 14 = 26 км. За другу годину перший лижник пройшов 12 км, а другий – 14 км, тому вони за другу годину наблизилися один до одного: 12 + 14 = 26 км.)

• Два велосипедисти виїхали одночасно з одного пункту в протилежних напрямах. Швидкість першого велосипедиста 5 , а другого – 3 . Як змінюється відстань між велосипедистами? ( Відстань при одночасному русі в протилежних напрямах весь час збільшується.)На скільки збільшиться відстань за 1-шу секунду, за 2-гу секунду ? ( 5 – це означає, що перший велосипедист за кожну секунду проїздив по 5 м; 3 – означає, що другий велосипедист за кожну секунду проїздив по 3 м. Отже, за першу секунду перший велосипедист відділився на 5 м, а другий – на 3 м, тому всього вони віддалилися один від одного : 5 + 3 = 8 м. За другу секунду перший велосипедист проїхав 5 м, а другий – 3 м, тому вони за другу секунду віддалилися один від одного: 5 + 3 = 8 м.)

3. Актуалізація правил та формул швидкості руху, часу руху та подоланого шляху.

Складіть за кожним рядком задачу і розв’яжіть ці задачі:

	S	V	t
Бджола	18 км	6	?
Бабка	200 км	?	2 год
Стриж	?	100	4 год

4. Індивідуальне опитування біля дошки з наступною колективною перевіркою.

У той час, поки відбувається усна лічба та усне опитування, учень біля дошки працює над задачею.

Машина їхала 3 год зі швидкістю 100 , і 4 год зі швидкістю 120 . Яку відстань подолала машина? ( Це задача на знаходження суми двох добутків.)

При колективній перевірці звертаємо увагу учнів на пояснення:

	S( км)	V( км/год)	t (год)
1	?	100	3 год.
	?
П	?	120	4 год.

Крім того до цієї задачі корисно зробити креслення:

• Що означає число 100? (Число 100 означає швидкість автомобіля першого разу. 100 означає, що автомобіль за кожну годину проїздив по 100 км.)

• Що означає число 3? ( Число 3 означає час руху автомобіля.)

• Отже автомобіль за першу годину подолав 100 км ( покажемо це відрізком), за другу годину подолав 100 км, за третю годину – 100 км.

• Що означає число 120? ( Число 120 означає швидкість автомобіля другого разу. 120 означає, що автомобіль за кожну годину проїздив по 120 км.)

• Що означає число 4? ( Число 4 означає час руху автомобіля другого разу.)

• Отже автомобіль за першу ( з 4-х годин) проїхав 120 км ( покажемо це відрізком), за другу годину – 120 км, за третю годину – 120 км, за четверту годину – 120 км.

• Яке число є шуканим? ( Шуканою є загальна відстань, яку подолав автомобіль за весь час руху.) Як це показати на кресленні? ( Фігурною дужкою.)

100 120

ІІІ. ПРОВЕДЕННЯ ДОСЛІДЖЕННЯ

1. Ознайомлення із задачами на одночасний рух назустріч на знаходження відстані між тілами на момент початку руху. Задача 1.

Завдання №1 виконується колективно.

Про що йде мова в задачі? ( В задачі йде мова про рух двох вершників.) Що відомо про час початку руху? (Вершники почали рухатися одночасно.) Як рухаються вершники? ( Вершники рухаються назустріч один одному.) Подивіться як це показано на кресленні стрілочками „назустріч”. Зробіть висновки. 1) Відстань між тілами весь час зменшується. 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. Чи відома швидкість першого вершника? Другого вершника? Зверніть увагу: над стрілочками записуємо швидкості руху кожного вершника. НА місті зустрічі поставлено прапорець Зверніть увагу: чому прапорець зміщено у бік другого вершника – швидкість другого вершника менше, ніж швидкість першого, на рух вони витратили однаковий час, тобто 3 год; значить другий пройшов менший шлях, ніж перший. Прапорець треба поставити ближче до другого селища. На рух кожний вершник витратив 3 години, оскільки вершники зустрілися через 3 години. Зверніть увагу: біля прапорця написано t = 3 год. Треба знайти відстань між селищами: її позначено фігурною дужкою. Нагадаємо, що вся відстань складається з шляху, який пройшов перший вершник та шляху, який пройшов другий вершник. Зверніть увагу: шлях, який подолав перший вершник позначено синьою фігурною дужкою: другий – червоною.)

За коротким записом поясніть числа задачі. ( Число 16 позначає швидкість першого вершника. 16 означає, що перший вершник за кожну годину долав по 16 км. Число 15 означає швидкість другого вершника. 15 означає, що за кожну годину другий вершник долає по 15 км. Число 3 означає час, який рухався кожний вершник.)

Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами? ( В задачі запитується про відстань між селищами. Відстань між селищами дорівнює усьому шляху, що подолали разом вершники. Отже, вся відстань складається з шляху, який подолав перший вершник та шляху, який пробіг другий. Щоб знайти подоланий шлях, треба швидкість руху тіла помножити на час руху.)

Яке запитання задачі? (Яка відстань між селищами?) Як ми його пере формулювали? ( Який шлях подолали обидва лижники разом?) Що треба знати , щоб відповісти на запитання задачі? ( Треба знати два числові значення: 1 – шлях, який подолав перший вершник , не відомо, та ІІ – шлях, який подолав другий , невідомо.) Якою арифметичною дією відповімо на запитання задачі? ( Дією додавання.) Чи можна відразу відповісти на запитання задачі? ( Не можна, тому що ми не знаємо: 1 – шлях, який подолав перший вершник та не знаємо ІІ – шлях, який подолав другий вершник.)

Що треба знати, щоб дізнатися про шлях, який подолав перший вершник? ( Треба знати два числові значення: 1 – швидкість першого вершника, відомо 16 , та ІІ – час руху першого вершника, відомо 3 год.) Якою арифметичною дією відповімо на це запитання? ( Дією множення.) Чи можна тепер відповісти на запитання задачі? ( Не можна, тому що ми не знаємо який шлях подолав другий вершник.)

Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – швидкість другого вершника, відомо 15 , та ІІ – час руху другого вершника, відомо 3 год.) Якою арифметичною дією відповімо на це запитання? ( Дією множення.) Чи можна тепер відповісти на запитання задачі? ( Так, ми від запитання задачі перейшли до числових даних. Аналіз закінчено.)

Складіть план розв’язування задачі. (Першою дією дізнаємося про шлях, який подолав перший вершник, дією множення. Другою дією дізнаємося про шлях, який подолав другий вершник, дією множення. Третьою дією дізнаємося про шлях, який подолали разом обидва вершники, а тому й про відстань між селищами і відповімо на запитання задачі, дією додавання.) Запишіть розв’язання по діях з поясненням.

Розв’язання

1. 16 * 3 = 48 ( км) – шлях, який подолав перший вершник, S₁;

2. 15 * 3 = 45 ( км) – шлях, який подолав перший вершник, S₂;

3. 48 + 45 = 93 ( км) – шлях, який подолали обидва вершники разом; відстань між селищами, S.

Відповідь: відстань між селищами 93 км.

2. З

   Зміна числових даних не вплине на план розв’язування задачі. План розв’язування лишиться тим самим. Першою дією дізнаємося про шлях, який подолав перший вершник, дією множення. Другою дією дізнаємося про шлях, який подолав другий вершник, дією множення. Третьою дією дізнаємося про шлях, який подолали разом обидва вершники, а тому й про відстань між селищами і відповімо на запитання задачі, дією додавання.

   міна числових даних задачі 1 і дослідження впливу зміни на розв’язання задачі.

4

60

90

3. Зміна напрямку руху тіл, одержання задачі на одночасний рух в протилежних напрямках (задача 2), та дослідження впливу цієї зміни на розв’язання задачі.

6

6

Що відомо про час початку руху? ( Лижники почали рухатися одночасно.) Як рухаються лижники? ( Лижники рухаються в протилежних напрямах.) Зробіть висновки. 1) Відстань між тілами весь час збільшується. 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. Виконуємо зміни у короткому записі: міняємо напрямок стрілочок. За коротким записом поясніть числа задачі. Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами?

Порівняйте цю задачу з попередньою. Чим вони відрізняються? ( В першій задачі вершники рухалися назустріч, а в цій – в протилежних напрямках.) Як ця зміна вплине на розв’язання задачі? Чи зміниться перша дія? Друга дія? Третя дія? Розкажи план розв’язання цієї задачі.

Першою дією дізнаються про відстань, яку пройшло перше тіло, дією множення.

Другою дією дізнаються про відстань, яку пройшло друге тіло, дією множення.

Третьою дією дізнаються про відстань, яку пройшли обидва тіла, дією додавання.

Отже, якщо в задачі треба знайти відстань при одночасному русі назустріч або в протилежних напрямках, то її розв’язують за планом:

4. З

   Зміна числових даних не вплине на план розв’язування задачі. План розв’язування лишиться тим самим. Першою дією дізнаємося про шлях, який подолав перший вершник, дією множення. Другою дією дізнаємося про шлях, який подолав другий вершник, дією множення. Третьою дією дізнаємося про шлях, який подолали разом обидва вершники, а тому й про відстань між селищами і відповімо на запитання задачі, дією додавання.

   міна числових даних задачі 2 та дослідження впливу цієї зміни на розв’язання задачі.

5. Заміна числових даних швидкостей тіл буквами та дослідження впливу цієї зміни на план розв’язання задачі.

Завдання №2 виконується колективно.

Заміна числових значень буквами не вплинула на план розв’язання задач: першою дією знаходимо відстань, що подолало перше тіло, другою дією – відстань, що подолало друге тіло і третьою дією знаходимо відстань, яку подолали обидва тіла. Читаємо пам’ятку, звертаємо увагу на запис арифметичних дій буквами.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння розв’язувати задачі на одночасний рух назустріч ( в протилежних напрямках) на знаходження відстані між тілами на момент початку (закінчення) руху.

Завдання №2 із робочого зошита. Диференційована робота над задачею.

Учні, які працювали самостійно над задачею одержують додаткове завдання: перетворити цю задачу на одночасний рух у протилежних напрямках; дослідити вплив цієї зміни на розв’язання задачі. За потреби можна запропонувати учням змінити числа задачі та дослідити вплив цієї зміни на розв’язання задачі.

2. Формування уміння виконувати письмове ділення та множення багатоцифрових чисел на двоцифрові.

Завдання № 3 виконується учнями самостійно.

Робота за сходинками складності: І виконати ділення на двоцифрове число; ІІ – виконати ділення на трицифрове число.

3. Розвиток логічного мислення учнів.

Магазин отримав зі складу 1000 лінійок. Одні з них мають довжину 20 см, а інші 30 см. Загальна довжина лінійок 220 м. Скільки 20-сантиметрових лінійок отримав магазин?

Розв’язання.

1. Якою була б загальна довжина лінійок, якби вони були усі 20-сантиметрові? 20 см х 1000 = 20000 см = 200 м.

2. Яка зайва загальна довжина, яка має місце тому, що серед лінійок є 30-сантиметрові? 220 м – 200 м = 20 м.

3. На скільки 30-сантиметрова лінійка довша за 20-сантиметрову? 30 – 20 = 10 ( см)

4. Скільки лінійок 30-сантиметрові? 20 м : 10 см = 2000см : 10 см = 200

5. Скільки лінійок 20-сантиметрові? 1000 – 200 = 800

Перевірка:

1. Яка загальна довжина 30-сантиметрових лінійок? 30 см х 200 =6000 см = 60м

2. Яка загальна довжина 20-сантиметрових лінійок? 20см х 800 =16000см =160м

3. Яка загальна довжина усіх лінійок? 60 + 160 = 220 ( м)

Відповідь: 800 лінійок.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання № 3 – виконати ділення письмово з перевіркою. Завдання №4 - розв’язати задачу, скориставшись пам’яткою.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Які випадки руху в різних напрямках існують? Що має бути дано у відповідних задачах? Що має бути шуканим? З чого складається вся відстань між селищами? Що можна сказати про спосіб розв’язування задач на одночасний рух назустріч та одночасний рух в протилежних напрямках на знаходження швидкості? Коли на уроці ви відчували складнощі? Що було зрозумілим? Що зацікавило?

Урок № 90/27 ( с. 48-49 )

Мета: формування уміння розв’язувати задачі на одночасний рух двох тіл в різних напрямках

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати спосіб розв’язування задач на одночасний рух двох тіл назустріч на знаходження відстані на момент початку руху; зміна шуканого задачі, одержання задачі на знаходження швидкості при одночасному русі назустріч й дослідити вплив цієї зміни на розв’язання задачі; змінити напрямок руху у задачі на знаходження швидкості одного з тіл для одержання задачі на рух у протилежні напрямки, дослідити вплив цієї зміни на розв’язання задачі. Узагальнити спосіб розв’язування задач на знаходження швидкості при одночасному русі двох тіл назустріч та у протилежних напрямках; вчити розв’язувати задачі з буквеними даними на основі узагальненого плану розв’язування задач цього типу. Формувати уміння розв’язувати задачі на знаходження швидкості одного з тіл під час одночасного руху двох тіл в різних напрямках. Вдосконалювати навичок письмового множення та ділення; вміння знаходити значення виразів на кілька дій.

Розвивальна задача: розвивати логічне мислення учнів під час дослідження задач та узагальнення способу їх розв’язування.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Ми тривалий час виконуємо дослідження. Пригадайте, що доводилось нам досліджувати в задачах на рух. Яким фахівцям у житті доводиться виконувати такі дослідження? Чи доводилось вам помічати щось подібне? Сьогодні ми виконаємо певні зміни в таких задачах і дослідимо, яким буде їх вплив на план розв’язування.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 із робочого зошита виконується учнями самостійно.

2. Усне опитування.

Що означає: легкова машина їде зі швидкістю 120 ? пліт пливе по річці зі швидкістю 4 ? швидкість велосипедиста 18 ? швидкість лижника 200 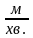? швидкість пароплаву 45 ? Земля рухається по орбіті зі швидкістю 30 ?

Чому дорівнює швидкість руху: пішохода, якщо він проходить 5 км за 1 годину ( 5 ) ; бджоли, якщо вона за кожну секунду пролітає 7 м; верблюда, якщо він в кожний час проходить 35 км; космічного корабля, якщо він у кожну секунду долає 8 км?

• Як зміниться швидкість руху, якщо час (подоланий шлях) збільшиться в кілька разів, а подоланий шлях (час) не зміниться? Як зміниться час руху, якщо швидкість руху ( подоланий шлях) зменшиться в кілька разів, а подоланий шлях ( швидкість) не зміниться?

• Як зміниться подоланий шлях, якщо швидкість (час) руху збільшиться у кілька разів, а час (швидкість( руху не зміниться?

• Які висновки можна зробити при одночасному русу назустріч ( у протилежні напрямки)?

• Із двох міст одночасно назустріч вирушили дві машини і зустрілися через 2 години. Скільки часу рухалась кожна машина? ( 2 години)

• З села в місто виїхав мотоцикліст і в цей же час із міста назустріч йому виїхав велосипедист, який зустрів мотоцикліста через 20 хвилин. Скільки часу рухався до зустрічі мотоцикліст? ( 20 хвилин)

• Два вершники вирушили одночасно в протилежних напрямках і закінчили свій рух через 45 хвилин. Скільки часу рухався кожний вершник? Що можна сказати про шлях, яку подолав кожний вершник, якщо:

• вони рухалися з однаковою швидкістю; ( відстань однакова, тому що швидкості однакові в обох вершників та час руху, теж однаковий .);

• швидкість першого більше швидкості другого; ( шлях, який пройшов перший вершник більший за шлях, який пройшов другий; при однаковому часі руху, швидкість і шлях змінюються одному напрямі: чим більше швидкість руху, тим більший шлях долає тіло).

• Два краби одночасно виринули назустріч одна одній. Швидкість першого краба 6 , а швидкість другого 8 . Як змінюється відстань між крабами? На скільки дм зменшується відстань між крабами за кожну хвилину?

• Два катери відійшли від пристані одночасно в протилежних напрямках. Швидкість першого катера 36 , а другого – 42 . Як змінюється відстань між катерами. На скільки кілометрів збільшується відстань між катерами за кожну годину? Складіть обернену задачу, в якій треба знайти швидкість першого катера.

• Два лижники вийшли з одного селища одночасно в протилежних напрямках. Знайдіть швидкість другого лижника, якщо швидкість першого лижника 5 і відомо, що вони віддаляються за кожну годину на 12 км.

• Хлопчик і дівчинка почали одночасно бігти на ковзанах. З якою швидкістю біжить дівчинка, якщо швидкість хлопчика 5 і вони наближаються один до одного на 9 м за кожну секунду?

3. Актуалізація уміння розв’язувати задачі на одночасний рух на зустріч на знаходження відстані між тілами на момент або початку руху.

Завдання №1 (1) колективна робота. Всі записи виконуються лише на дошці.

• Про що йде мова в задачі? Що відомо про час початку руху?

• Як рухаються велосипедисти? Покажемо це на кресленні стрілочками „назустріч”. Зробіть висновки.

• Складіть короткий запис задачі.

• За коротким записом поясніть числа задачі.

• Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами?

• Яке запитання задачі? Як ми його пере формулювали?

• Розкажіть план розв’язування задачі.

10

11

2

Розв’язання

1. 10 * 2 = 20 ( км) – шлях, який подолав перший велосипедист, S₁;

2. 11 * 2 = 22 ( км) – шлях, який подолав перший велосипедист, S₂;

3. 20 + 22 = 42 ( км) – шлях, який подолали обидва велосипедисти разом; відстань між містами, S.

ІІІ. ПРОВЕДЕННЯ ДОСЛІДЖЕННЯ

1. Ознайомлення із задачами на одночасний рух назустріч на знаходження швидкості руху одного з тіл. Задача 2.

Завдання №1 (обернена задача) виконується колективно.

Пояснюємо, як внесено зміни у короткий запис задачі у підручнику; паралельно вносимо зміни у короткий запис задачі 1, записаний на дошці. За коротким записом поясніть числа задачі. ( Число 10 позначає швидкість брички. 10 означає, що перший велосипедист за кожну годину проїздила по 10 км. Число 2 означає час, який рухався перший велосипедист і час, який рухалася другий, та час їх зустрічі. Число 42 означає відстань між містами, шлях, який подолали разом обидва велосипедисти.) Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами? ( В задачі запитується про швидкість другого велосипедиста. Щоб знайти швидкість другого , треба шлях, що подолав другий велосипедист поділити на час його руху.) Що треба знати , щоб відповісти на запитання задачі? ( Треба знати два числові значення: 1 – шлях, який подолав другий велосипедист , не відомо, та ІІ – час руху другого велосипедиста, відомо, 2 год.) Якою арифметичною дією відповімо на запитання задачі? ( Дією ділення.) Чи можна відразу відповісти на запитання задачі? ( Не можна, тому що ми не знаємо: 1 – шлях, який подолав другий велосипедист до зустрічі)

Що треба знати, щоб дізнатися про відстань, яку подолав другий велосипедист до зустрічі? ( Треба знати два числові значення: 1 – загальний шлях, який подолали обидва велосипедисти, відомо 42 км , та ІІ – шлях, який подолав перший велосипедист, невідомо.) Якою арифметичною дією відповімо на це запитання? ( Дією віднімання.) Чи можна відразу відповісти на це запитання? ( Не можна, тому що ми не знаємо яку шлях, який подолав перший велосипедист.)

Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – швидкість першого велосипедиста , відомо 10 , та П – час руху першого велосипедиста, відомо 2 год.) Якою арифметичною дією відповімо на це запитання? ( Дією множення.) Чи можна тепер відповісти на запитання задачі? ( Так, ми від запитання задачі перейшли до числових даних. Аналіз закінчено.)

Складіть план розв’язування задачі. (Першою дією дізнаємося про шлях, який подолав перший велосипедист, дією множення. Другою дією дізнаємося про шлях, який подолав другий велосипедист, дією віднімання. Третьою дією дізнаємося про швидкість другого велосипедиста і відповімо на запитання задачі, дією ділення.)

Отже, у розв’язанні першої задачі, що записано на дошці, перша дія лишається тією самою, змінюється друга дія, але пояснення лишаються тими самими; звичайно, змінюється третя дія, оскільки змінилося шукане. Вносимо зміни у розв’язання задачі 1, записане на дошці.

Розв’язання

4. 10 * 2 = 20 ( км) – шлях, який подолав перший велосипедист, S₁;

5. 42 - 20 = 22 ( км) – шлях, який подолав перший велосипедист, S₂;

6. 22 : 2 = 11 ( ) – швидкість другого велосипедиста, V₂.

2. Зміна напрямку руху в задачі 2 – тіла рухаються у протилежних напрямках. Дослідження впливу цієї зміни на план розв’язання задачі.

Пояснюємо поданий у підручнику короткий запис задачі і вносимо зміни у короткому записі задачі 2 на дошці.

Що відомо про час початку руху? Як вони рухаються ? Зробіть висновки. За коротким записом поясніть числа задачі. Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами? ( В задачі запитується про швидкість другого велосипедиста. Щоб знайти швидкість другого велосипедиста, треба шлях, який він подолав поділити на час його руху.)

Порівняйте цю задачу з попередньою. Чим вони відрізняються? Як ця зміна вплине на розв’язання задачі? Чи потрібно її розв’язувати? Розкажи план розв’язання цієї задачі.

О

Першою дією дізнаються про шлях, який подолало одне тіло, дією множення.

Другою дією дізнаються про шлях, який подолало інше тіло, дією віднімання.

Третьою дією дізнаються про швидкість тіла, дією ділення.

тже, якщо в задачі треба знайти швидкість при одночасному русі назустріч або в протилежних напрямах, то її розв’язують за планом:

3. Заміна числових даних швидкості одного з тіл та відстані буквами та дослідження впливу цієї зміни на план розв’язання задачі.

Завдання № 2 виконується колективно.

Заміна числових значень буквами не вплинула на план розв’язання задач: першою дією знаходимо відстань, що подолало одне тіло, другою дією – відстань, що подолало інше тіло і третьою дією знаходимо швидкість іншого тіла і відповідаємо на запитання задачі. Звертаємо увагу на пам’ятку, подану в підручнику та запис арифметичних дій буквами.

4. Узагальнення планів розв’язання задач на знаходження відстані та на знаходження швидкості при одночасному русі назустріч та у протилежних напрямках. Формулювання першого способу розв’язання цих задач.

Завдання № 2 , 3 із робочого зошита. Диференційована робота над задачею.

Учням, які працювали самостійно пропонуємо додаткове завдання: визначити спільне і відмінне у планах розв’язування задач на одночасний рух У різних напрямках на знаходження відстані між тілами та на знаходження швидкості одного з тіл.

Навч. Зош. 3 частина с. 7

Зазначимо, що над задачами на рух працюємо за пам’яткою:

Пам’ятка ( 1 спосіб: s, V )

1. Про що йде мова в задачі?

2. Що відомо про час початку руху?

3. Як рухаються тіла?

4. Зробіть висновки.

1. Відстань між тілами весь час .

2. Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло.

3. Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно.

5. Складіть короткий запис задачі.

6. За коротким записом поясніть числа задачі.

7. Складіть план розв’язування задачі.

Першою дією визначають відстань, яку пройшло перше тіло.

Другою дією визначають відстань, яку пройшло друге тіло.

Третьою дією відповідають на запитання задачі.

8. Запишіть розв’язання по діях з поясненням або виразом.

9. Запишіть відповідь до задачі.

10. Складіть і розв’яжіть обернену задачу (на знаходження ) або перетворіть задачу у задачу на .

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння виконувати письмове ділення та множення багатоцифрового числа на двоцифрове.

Завдання № 4 виконується учнями самостійно.

2. Вдосконалення уміння знаходити значення виразів на кілька дій.

Завдання №4 із робочого зошита виконується учнями самостійно.

3. Розвиток логічного мислення учнів.

На спортивному майданчику лісового містечка спортсмени вишукувалися в наступному порядку:

Заєць – Білка – Вовк – Лисиця – Лось – Ведмідь.

Головний суддя Єнот запропонував усім вишукуватися за зростом, починаючи з найвищого:

Лось – Ведмідь – Вовк – Лисиця – Заєць – Білка.

Дозволялося мінятися місцями лише тим, що поряд стоять парами й переходити на нове місце, проходячи пару звірів, що стоять поряд. За яке найменше число таких переходів можна було б вишукуватися за зростом ?

Розв’язання. Проводимо одне із можливих переміщень:

1. Заєць – Білка – Лось – Ведмідь – Вовк – Лисиця.

2. Лось – Ведмідь – Заєць – Білка – Вовк – Лисиця.

3. Лось – Ведмідь – Вовк – Лисиця – заєць – Білка.

Відповідь: всього 3 переміщення.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №3 – розв’язати задачу, скориставшись пам’яткою. Завдання № 4 – виконати обчислення письмово та перевірити одержаний результат.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Які варіанти руху тіл в різних напрямках існують? Що може бути шуканим у задачах на рух в різних напрямках? Як можна міркувати при розв’язуванні задачі на знаходження відстані на момент закінчення руху ( на момент початку руху)? Як можна міркувати при розв’язуванні задачі на знаходження швидкості одного з тіл при одночасному русі в різних напрямках? Що спільне у планах розв’язування задач на знаходження відстані між тілами та на знаходження швидкості одно з тіл? Коли на уроці відчували ускладнення? Що в роботі вас втішило?

Урок № 91/28 ( с.50-51)

Мета: формувати уміння розв’язувати задачі на одночасний рух двох тіл в різних напрямках

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати спосіб знаходження зміни відстані між тілами за одиницю часу при одночасному русі у протилежні напрямки; спосіб розв’язування задач на одночасний рух двох тіл в протилежних напрямках на знаходження відстані; зіставити задачі 1 і 2, з’ясувати можливості розв’язування задачі 2 іншим способом; дослідити вплив відмінності між задачами 1 і 2 на розв’язання задачі 2 іншим способом; зміни напрямку руху тіл у задачі 2, дослідити вплив цієї зміни на розв’язання задачі; розв’язання задачі на знаходження відстані між тілами при одночасному русі назустріч двома способами; узагальнити два способи розв’язування задач на знаходження відстані при одночасному русі двох тіл назустріч та у протилежних напрямках. Змінити шукане задачі 2 для одержання задачі на одночасний рух в протилежних напрямках на знаходження швидкості одного з тіл, дослідити вплив цієї зміни на розв’язання задачі ІІ-м способом; змінити напрямок руху тіл в одержаній задачі і дослідити вплив цієї зміни на план розв’язування задач ІІ-м способом на знаходження швидкості одного з тіл при одночасному русі назустріч; узагальнити два способи розв’язування задач на знаходження швидкості одного з тіл при одночасному русі назустріч та у протилежні напрямки. Формувати уміння розв’язувати задачі на знаходження відстані між тілами та на знаходження швидкості одного з тіл при одночасному русі в різних напрямках ( назустріч та у протилежних напрямках). Вдосконалювати навичок письмового множення та ділення.

Розвивальна задача: розвивати логічне мислення учнів під час дослідження задач та узагальнення способів їх розв’язування.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Сьогодні ми продовжимо досліджувати задачі. Зазвичай будь-яке дослідження завершується винаходом, відкриттям чогось нового для дослідника. Вам може здається, що ви вже все знаєте про розв’язування задач на рух. Проте, ще лишилися «білі плями». Наприклад, вам відомо, що деякі задачі можна розв’язати кількома способами? Може і задачі на рух на знаходження відстані між тілами та швидкості руху одного з тіл, так само, можна розв’язувати кількома способами? А вам відомий поки що один спосіб розв’язування. Сьогодні на уроці ми відкриємо другий спосіб розв’язування таких задач.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №4 виконується учнями самостійно.

2. Усне опитування:

• Що означає: черепаха повезе зі швидкістю 3 ? ластівка летить зі швидкістю а ?

• Чому дорівнює швидкість руху: поїзду, якщо він проїжджає за кожну хвилину 15 км? ( 15 ); літака, якщо він за годину, пролетів 870 км? ( 870 ); лижника, якщо він за хвилину пройшов в м? ( в ).

• Як зміниться швидкість руху, якщо час (подоланий шлях) збільшиться в кілька разів, а подоланий шлях (час) не зміниться? Як зміниться час руху, якщо швидкість руху (подоланий шлях) зменшиться в кілька разів, а подоланий шлях (швидкість) не зміниться?

• Як зміниться подоланий шлях, якщо швидкість (час) руху збільшиться у кілька разів, а час (швидкість) руху не зміниться?

• Які висновки можна зробити при одночасному русу назустріч (у протилежні напрямки)?

• Два равлики одночасно вирушили від гілки у протилежних напрямках. Швидкість першого равлика 6 , а швидкість другого 5 . Як змінюється відстань між равликами? На скільки метрів збільшується відстань між равликами щогодини?

• Два скутери відійшли від двох пірсів одночасно назустріч один одному. Швидкість першого скутера 750 , а другого – 730 . Як змінюється відстань між скутерами. На скільки кілометрів збільшується відстань між скутерами за кожну хвилину? Складіть обернену задачу, в якій треба знайти швидкість першого скутера.

• Дві машини виїхали одночасно вирушили в протилежних напрямах. Знайди швидкість другої машини, якщо відома швидкість першої 50 і відомо, що вони віддаляються за кожну годину на 120 км.

ІІІ. ПРОВЕДЕННЯ ДОСЛІДЖЕННЯ

1. Ознайомлення з другим способом розв’язування задач на одночасний рух в різних напрямках на знаходження відстані між тілами.

Завдання №1 виконується колективно.

1

Розв’язання

5 + 3 = 8 (м) – на стільки віддаляються мисливець і борсук щосекунди.

) Що означає число 3? Число 5? На скільки метрів щосекунди віддаляється борсук від мисливця щосекунди? На скільки метрів віддаляється мисливець від борсука щосекунди? На скільки метрів вони разом віддаляються один від одного щосекунди? Відповіді на запитання ілюструємо на кресленні на дошці.

2) Читаємо задачу 2); пояснюємо поданий у підручнику короткий запис; перетворюємо короткий запис задачі 1, поданий на дошці, на короткий запис задачі 2. В результаті зіставлення задач 1 і 2 доходимо висновку, що в задачах 1 і 2 однакові умови, але різні вимоги; задача 2 є продовженням задачі 1. З’ясовуємо, що для відповіді на запитання задачі 2 треба виконати ще одну арифметичну дію ( 8 * 45 = 360 (м)); дописуємо у розв’язанні задачі 1, поданому на дошці, ще одну арифметичну дію. Пояснюємо розв’язання, подане у підручнику.

2. Зміна напрямку руху в задачі 2 – тіла рухаються назустріч. Дослідження впливу цієї зміни на другий спосіб розв’язання. Задача 3.

Учні пояснюють числа задачі та шукане за коротким записом, поданим на с. 51 підручника. За коротким записом поясніть числа задачі. Спочатку розв’яжемо цю задачу другим способом:

Яке запитання задачі? Як можна його пере формулювати? ( Запитання: Яка відстань між дітьми буде через 45 с можна пере формулювати так – на скільки зменшиться відстань між мисливцем та борсуком через 45 с?)

Що треба знати, щоб відповісти на запитання задачі? ( Треба знати два числові значення: 1 – на скільки кілометрів зменшується відстань між мисливцем і борсуком за кожну секунду , не відомо, та ІІ – час руху, відомо, 45 с.) Якою арифметичною дією відповімо на запитання задачі? ( Дією множення.) Чи можна відразу відповісти на запитання задачі? ( Не можна, тому що ми не знаємо: на скільки зменшується відстань між мисливцем і борсуком за кожну годину.)

Що треба знати, щоб про це дізнатися ? ( Треба знати два числові значення: 1 – відстань, на яку наближається мисливець до борсука щосекунди, відомо 5 м , та ІІ – відстань, на яку наближається борсук до мисливця щосекунди, відомо 3 м.) Якою арифметичною дією відповімо на це запитання? ( Дією додавання.) Чи можна відразу відповісти на це запитання? ( Так, ми від запитання задачі перейшли до числових даних. Аналіз закінчено.)

?

? * 45

5 + 3

- Складіть план розв’язування задачі. (Першою дією дізнаємося на скільки метрів зменшується відстань між мисливцем і борсуком, дією додавання. Другою дією дізнаємося на скільки зменшиться відстань між ним за 3 години і відповімо на запитання задачі.) Учні самостійно записують розв’язання задачі у зошитах.

Отже, розв’язання задачі, записане на дошці, майже, не змінюється. Всі відмінність у поясненнях: мисливець і борсук не віддаляються, а наближаються один до одного. У поясненнях до арифметичних дій, у розв’язанні на дошці, виправляємо слова «віддаляється» на «наближається». Узагальнюємо ІІ спосіб розв’язування задач на одночасний рух на знаходження відстані між тілами за умов руху назустріч та за умов руху у протилежних напрямках.

Розв’язання

1. 5 * 45 = 225 ( м) - шлях, який подолав мисливець;

2. 3 * 45 = 135 ( м) - шлях, яку подолав борсук;

3. 225 + 135 = 360 ( м) - шлях, який подолали разом мисливець і борсук, відстань між ними на момент початку руху.