Задания для самостоятельной работы:
Найти
и
,
если:
;
;
;
;
;
;
;
;
;
;;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Найти и
,
если:
;
;
;
;
;
;; ;
;
;
;
;; ;
;
;
;
;
;
;;
;
;
;;
;;
;; ;
;
;
;
;
;
;
;
;;
;; ;
;
;;
;;
;;
;; ;
;
;;
;
;
;
;
.
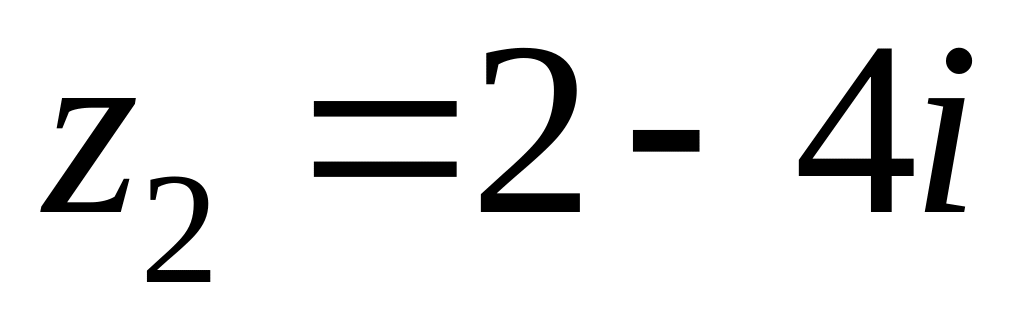Вычислить:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
Решить уравнения:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;;
;
;
.
Составить приведенное квадратное уравнение с действительными коэффициентами, имеющее данный корень:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
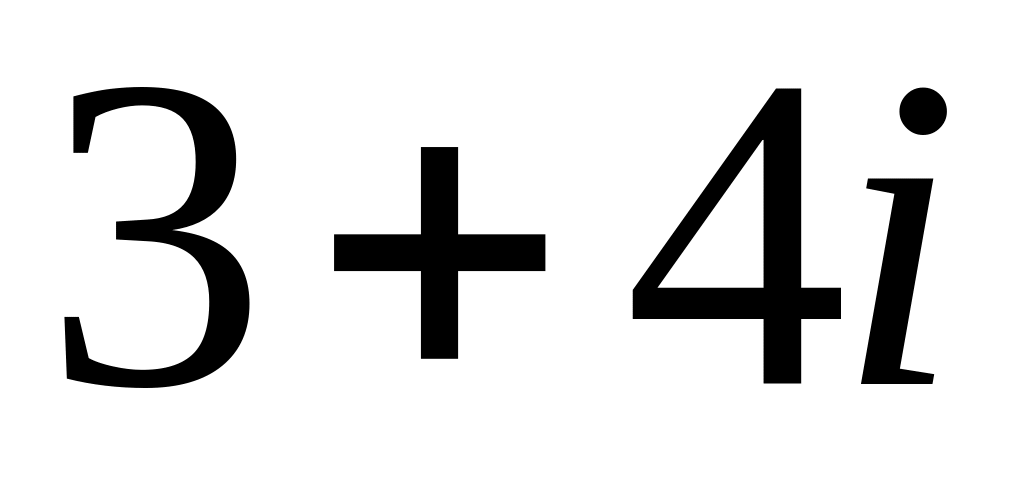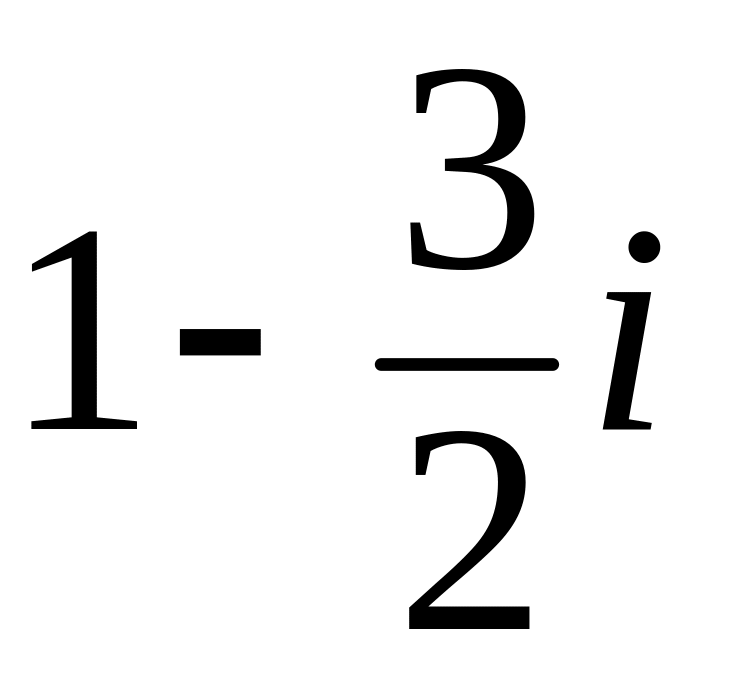Геометрическое представление комплексных чисел. Модуль и аргументы комплексного числа
Основные определения
Часто бывает удобно рассматривать комплексное число
как вектор
,
имеющий начало в начале координат
и конец в точке
(рис. 1).
Рис. 1. Геометрическое представление комплексного числа
Положение точки
может быть определено расстоянием
от начала координат и углом
- углом наклона радиус-вектора к
положительному направлению оси ОХ.
Модулем комплексного
числа
называется неотрицательное действительное
число, равное модулю (длине) соответствующего
этому числу вектора
.
Модуль числа
обозначается символом
или буквой
.
По теореме Пифагора получаем формулу
для вычисления модуля
.
Заметим, что модуль
комплексного числа
совпадает с модулем (абсолютной
величиной) действительного числа
:
.
Комплексным
числам, имеющим один и тот же модуль,
соответствуют точки комплексной
плоскости, лежащие на окружности радиуса
с центром в начале координат.
Пример 5. Найдём
модуль комплексного числа
.
.
Аргументом
комплексного числа
называется значение угла
между положительным направлением
действительной оси и вектором
,
причём, значение угла
считается положительным, если отсчёт
ведётся против часовой стрелки, и
отрицательным, если отсчёт производится
по часовой стрелке. Заданием модуля и
аргумента комплексное число определяется
однозначно. Для числа
аргумент не определяется, но в этом и
только в этом случае число задаётся
только своим модулем.
Аргумент комплексного
числа, в отличие от модуля, определяется
неоднозначно. Например, аргументами
числа
являются следующие углы:
,
,
и, вообще каждый
из углов
,
где
- произвольное целое число (рис. 2).
Рис. 2. Аргументы комплексного числа:
а)
;
б)
;
в)
Пусть
- угол, удовлетворяющий неравенствам
.
Тогда каждому комплексному числу соответствует один угол такого вида, он называется главным значением аргумента и обозначается
.
Множество всех других значений аргумента обозначают символом
.
Пример 6. Найдём
аргументы комплексных чисел
,
,
.
Построив векторы
,
,
(рис. 3), находим главное значение
аргумента для каждого числа.
Рис. 3. Аргументы чисел –i, 1, -1+i
,
,
.
Тогда,
,
,
,
-
целое число.
Действительная и мнимая части комплексного числа выражаются через его модуль и аргумент следующим образом:
,
.
Таким образом, аргумент комплексного числа может быть найден как решение системы уравнений
.
Пример 7. Найдём
аргумент комплексного числа
.
Здесь
,
,
,
.
Решая эту систему, найдём
,
,
Аргумент комплексного числа можно найти иначе:
.
Это уравнение не равносильно системе, оно имеет больше решений. Однако выбор аргумента упрощается, если установить в каком квадранте комплексной плоскости расположено число.
Пример 8. Найдём
аргумент комплексного числа
.
,
откуда
,
.
Так как комплексное число расположено в четвёртом квадранте, то
(рис. 4).
Рис. 4. Аргумент комплексного числа
