Федеральное агентство железнодорожного транспорта

Федеральное государственное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

________________________________________________________________

Кафедра «Экономика транспорта»

ЭКОНОМЕТРИКА

Методические указания к практическим занятиям

Часть I

САНКТ-ПЕТЕРБУРГ

ПГУПС

2014

Предназначены для студентов-бакалавров, обучающихся по направлению 080100.62 «Экономика» профиль «Экономика предприятий и организаций» (транспорт).

Лабораторная работа № 1 парная линейная и нелинейная корреляция

Социально-экономические явления, обладая большим разнообразием, характеризуются множеством признаков, отражающих те или иные их свойства. При этом для данных явлений характерно то, что наряду с существенными факторами на них оказывают воздей­ствие многие другие, в том числе случайные факторы. В этом случае говорят о статистической зависимости.

Частным случаем статистической зависимости является кор­реляционная зависимость, имеющая огромное значение в эконометрике. Корреляционная зависимость – это связь, при которой каждому значению не­зависимой переменной х соответствует определенное математическое ожидание (среднее значение) зависимой переменной у. Корреляция между двумя переменными может быть линейной и нелинейной.

Аналитически линейная корреляция определяется уравнением прямой:

(1.1)

К нелинейным относятся все другие виды корреляционных зависимостей, аналитически выражаемых уравнениями вида:

, , и т.п.

Тесноту линейной связи между двумя коррелирующими переменными без разделения их на зависимую и независимую переменные характеризуют линейным коэффициентом парной корреляции :

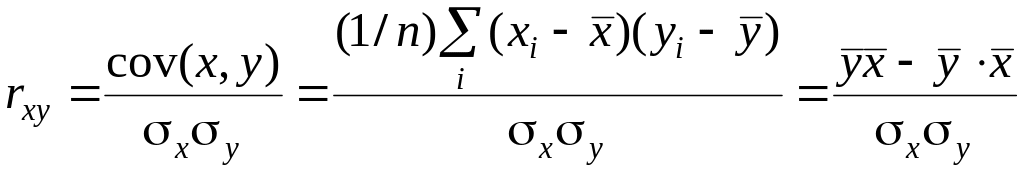, (1.2)

где – данные наблюдений переменных и ; – количество наблюдений; – средние значения переменных и (простое среднее арифметическое); – средние квадратические отклонения переменных и :

, . (1.3)

Линейный коэффициент парной корреляции изменяется в диапазоне . При связь между переменными является прямой, при связь обратная. Чем ближе к 1, тем теснее линейная связь между переменными и тем точнее аналитическое уравнение отражает данные наблюдений.

Часто используется следующая градация степени тесноты связи парной линейной корреляции: – связь практически отсутствует, – связь слабая, – связь умеренная, – связь сильная, – связь функциональная.

Теснота нелинейной связи между двумя коррелирующими переменными характеризуется индексом корреляции :

, (1.4)

где – расчётные значения переменной , т.е. значения переменной , вычисленные по уравнению нелинейной связи .

Индекс корреляции принимает значения в диапазоне . Чем ближе величина к 1, тем теснее нелинейная связь. При нелинейная связь является функциональной.

Для оценки статистической значимости линейного коэффициента парной корреляции используют расчётный критерий Стьюдента

. (1.5)

Значение сравнивается с критическим табличным значением критерия Стьюдента для количества степеней свободы и заданного уровня значимости . Если , то значение признается статистически значимым, в противном случае – статистически незначимым.

Уровень значимости статистического теста представляет собой вероятность отвергнуть нулевую статистическую гипотезу (обычно принимается на уровне 0,05 или 0,01), если она верна.

Для оценки статистической значимости индекса корреляции используется расчётное значение F-критерия Фишера

. (1.6)

сравнивается с критическим табличным значением критерия Фишера для количества степеней свободы , и заданного уровня значимости . Если , то значение признается статистически значимым, в противном случае – статистически незначимым.

Помимо проверки значимости полученного значения линейного коэффициента парной корреляции важное значение имеет построение доверительного интервала для . Доверительный интервал характеризует границы, в которых находится точное значение оцениваемого показателя с заданной вероятностью .

При построении доверительного интервала для сначала производится расчёт величины с использованием Z-преобразования Фишера

. (1.7)

Далее производится интервальная оценка для величины

, (1.8)

где , рассчитанное по формуле 1.7; – квентиль стандартного нормального распределения порядка .

Границы доверительного интервала для рассчитываются на основе границ доверительного интервала для с использованием обратного Z-преобразования Фишера :

, . (1.9)