
- •Введение
- •1. Физические свойства жидкости
- •2. Гидростатика
- •2.1. Гидростатическое давление и его свойства
- •2.2. Силы давления жидкости на плоские поверхности
- •2.3. Сила давления жидкости на криволинейные стенки
- •2.4. Эпюры гидростатического давления
- •2.5. Относительный покой жидкости
- •Приложение 1 Средние значения плотности и кинематической вязкости некоторых жидкостей
- •3. Гидродинамика
- •3.1. Основные понятия
- •3.2. Уравнение неразрывности
- •3.3. Уравнение Бернулли для элементарной струйки идеальной жидкости
- •3.4. Уравнение Бернулли для элементарной струйки реальной жидкости
- •3.5. Уравнение Бернулли для потока реальной жидкости
- •3.6. Режимы течения жидкости.
- •3.7. Потери на трение при движении жидкости
- •3.7.1. Потери на трение по длине
- •3.7.2 Потери напора в местных сопротивлениях
- •3.8. Истечение жидкости через отверстия и насадки
- •3.8.1 Истечение жидкости из отверстия в тонкой стенке
- •3.8.2 Истечение жидкости из насадков
- •Примеры решения задач
- •Зависимость плотности воды от температуры
- •Средние значения плотности и кинематической вязкости некоторых жидкостей
- •Средние значения эквивалентной шероховатости
- •4. Основы расчета трубопроводов
- •4.1. Тип трубопроводов и их классификация
- •4.2. Расчет гидравлически длинного трубопровода постоянного диаметра
- •4.3. Расчет трубопровода из последовательно соединенных труб
- •4.4. Расчет параллельного соединения труб
- •4.5. Расчет трубопровода с непрерывным распределением расхода по длине
- •4.6. Расчет коротких трубопроводов
- •4.6.1. Расчет всасывающего трубопровода
- •4.6.2. Расчет сифонного трубопровода
- •Примеры решения задач
- •Значения эквивалентной равномерно-зернистой шероховатости kэ
- •Значения модуля расхода к и коэффициента гидравлического трения
- •(Квадратичная область сопротивления)
- •Значения модуля расхода к и коэффициента гидравлического трения
- •(Квадратичная область сопротивления)
- •Значения модуля расхода к и коэффициента гидравлического трения
- •(Квадратичная область сопротивления)
- •Расчетные значения удельных сопротивлений а для неновых стальных и чугунных водопроводных труб (размеры даны в мм)
- •Стальных и чугунных водопроводных труб (размеры даны в мм)
- •Библиографический список
- •Оглавление
- •1. Физические свойства жидкости 4
3.2. Уравнение неразрывности
Для
жидкости, текущей вдоль стенок, ее
ограничивающих, можно применить закон
сохранения материи, из которого следует:
количество втекающей жидкости в канал
равно количеству жидкости, из него
вытекающей, то есть расход – величина
постоянная для любого сечения участка
канала:
![]() .
Из определения средней скорости следует:
.
Из определения средней скорости следует:
![]()
Это
уравнение носит название уравнения
неразрывности. Его можно преобразовать
в следующее:
![]() .
.
3.3. Уравнение Бернулли для элементарной струйки идеальной жидкости
Если применить закон сохранения энергии для единицы массы стационарно движущейся идеальной жидкости, то можно сделать вывод: и в сечении 1-1 и в сечении 2-2 (рис. 17) жидкость обладает одинаковой удельной (отнесенной к единице массы) энергией.

Рис. 17
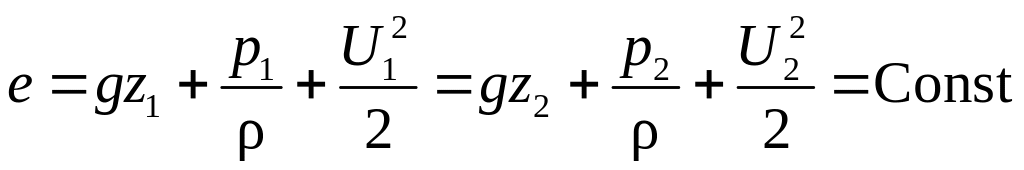 , (3)
, (3)
где gz
( )
– удельная потенциальная энергия
положения
)
– удельная потенциальная энергия
положения
![]() (
(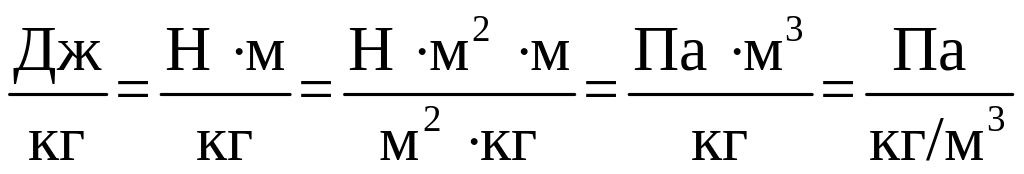 )
– удельная потенциальная энергия
давления
)
– удельная потенциальная энергия
давления
![]() (
( )
– удельная кинетическая энергия.
)
– удельная кинетическая энергия.
Изменение одной составляющей удельной энергии движущейся жидкости приводит к противоположному изменению других составляющих.
Уравнение Бернулли можно записать в следующем виде (разделим все члены уравнения на ускорение свободного падения g):
 ,
,
Первое слагаемое z представляет собой геометрический напор – высоту расположения потока над нулевой плоскостью.
Второе – пьезометрический напор p/(g) – расстояние от центра тяжести живого сечения до уровня жидкости в пьезометре. По уровню определяют давление жидкости в данном сечении.
Третье
– скоростной напор
![]() .
Определяется как разность уровней
жидкости в трубке Пито и пьезометре
(Рис.18). По показаниям трубки Пито
определяются два слагаемых в уравнении
Бернулли
.
Определяется как разность уровней
жидкости в трубке Пито и пьезометре
(Рис.18). По показаниям трубки Пито
определяются два слагаемых в уравнении
Бернулли
![]() (рис. 18).
(рис. 18).

Рис. 18
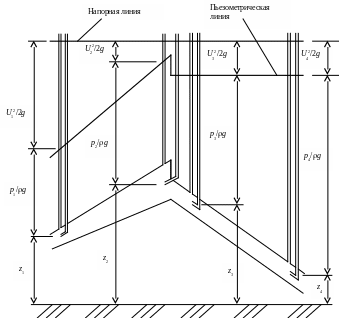
Таким образом, сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль потока идеальной жидкости. В этом заключается геометрическая интерпретация уравнения Бернулли (рис. 19).
Напорная линия, проходящая по уровням жидкости в трубках Пито, представляет собой горизонтальную прямую. Тогда как линия, проходящая по уровням жидкости в пьезометрах, или пьезометрическая линия, может располагаться различными способами, в зависимости от формы и расположения канала.
Умножив все члены уравнения (3) на , получим уравнение Бернулли, все члены которого выражены в единицах давления (Па):
![]()
где gz – весовое давление,
p – гидромеханическое давление, или просто давление,
![]() – динамическое давление.
– динамическое давление.
Рис. 19
3.4. Уравнение Бернулли для элементарной струйки реальной жидкости
Реальная жидкость обладает вязкостью, которая при движении жидкости вызывает появление внутреннего (трение струек жидкости друг о друга) и внешнего (о стенки) трения. Трение приводит к потерям энергии. Поэтому происходит постоянное уменьшение энергии потока жидкости вдоль течения.
 ,
,
где
![]() – потери удельной энергии на преодоление
сил трения при движении жидкости от
сечения 1-1 до сечения 2-2.
– потери удельной энергии на преодоление
сил трения при движении жидкости от
сечения 1-1 до сечения 2-2.
