
Глава 5 метод планирования экспериментов в обеспечении качества поверхностим деталей машин
Существует
несколько способов постановки факторных
экспериментов, для которых разработаны
сокращенные методы вычислений
[1,4–6,9,10]. Одним из них является эксперимент,
включающий факторы, каждый из которых
устанавливается только на двух уровнях:
верхнем ( + 1) и нижнем (–1). Такие эксперименты
называют факторными типа
 .
Общее число опытов в таких экспериментах
равно
,
т. е. удваивается с каждым новым фактором.
При большом числе факторов может
оказаться невозможным провести все эти
опыты. В этом случае получают заслуживающие
внимания результаты, выполняя определенную
часть опытов, так называемую дробную
реплику от полного факторного эксперимента.
При этом эффекты взаимодействий высших
порядков, чаще всего оказывающиеся
малозначимыми, смешиваются с эффектами
факторов. Для обозначения дробных
реплик, в которых
.
Общее число опытов в таких экспериментах
равно
,
т. е. удваивается с каждым новым фактором.
При большом числе факторов может
оказаться невозможным провести все эти
опыты. В этом случае получают заслуживающие
внимания результаты, выполняя определенную
часть опытов, так называемую дробную
реплику от полного факторного эксперимента.
При этом эффекты взаимодействий высших
порядков, чаще всего оказывающиеся
малозначимыми, смешиваются с эффектами
факторов. Для обозначения дробных
реплик, в которых
 эффектов факторов смешиваются с эффектами
взаимодействий, пользуются условным
обозначением
эффектов факторов смешиваются с эффектами
взаимодействий, пользуются условным
обозначением
 .
.
5.1. Основы метода планирования экспериментов
 Рассмотрим
сначала эксперименты
Рассмотрим
сначала эксперименты
 с
с
 повторениями (табл.5.1). Традиционное
представление плана таких экспериментов
заменяют матрицей планирования
(табл.
5.2). Эффект фактора (его влияние на
переменную) можно определить как
изменение отклика при изменении уровня
этого фактора. Так, если фактор
повторениями (табл.5.1). Традиционное
представление плана таких экспериментов
заменяют матрицей планирования
(табл.
5.2). Эффект фактора (его влияние на
переменную) можно определить как
изменение отклика при изменении уровня
этого фактора. Так, если фактор
 находится на нижнем уровне, влияние
фактора
находится на нижнем уровне, влияние
фактора
 равно
равно
 ;
при верхнем уровне фактора
влияние фактора
составляет
;
при верхнем уровне фактора
влияние фактора
составляет
 .
Следовательно, общий эффект фактора
,
так называемый контраст, находим как
.
Следовательно, общий эффект фактора
,
так называемый контраст, находим как
 (5.1)
(5.1)
Контраст фактора :
 (5.2)
(5.2)
Контраст взаимодействия :
 (5.3)
(5.3)
Таблица 5.2. Матрица планирования эксперимента
Номер опыта j |
|
|
|
|
|
1 |
-1 |
-1 |
+1 |
|
|
2 |
+1 |
-1 |
-1 |
|
|
3 |
-1 |
+1 |
-1 |
|
|
4 |
+1 |
+1 |
+1 |
|
|
Примечание. – суммарное значение переменных .
В
рассматриваемых уравнениях суммарные
значения откликов
 складываются алгебраически со знаками,
соответствующими значениям уровней
факторов и взаимодействий. Используя
значения контрастов, вычисляем суммы
квадратов для факторов и взаимодействия,
необходимые для дисперсионного анализа
экспериментальных данных:
складываются алгебраически со знаками,
соответствующими значениям уровней
факторов и взаимодействий. Используя
значения контрастов, вычисляем суммы
квадратов для факторов и взаимодействия,
необходимые для дисперсионного анализа
экспериментальных данных:



 (5.4)
(5.4)
Рассмотрим
эксперимент
 с
повторениями. Матрица планирования
такого эксперимента представлена в
табл. 5.3.
с
повторениями. Матрица планирования
такого эксперимента представлена в
табл. 5.3.
Таблица 5.3. Матрица планирования эксперимента
Номер опыта j |
|
|
|
|
|
|
|
|
|
1 |
–1 |
–1 |
–1 |
+1 |
+1 |
+1 |
–1 |
|
|
2 |
+1 |
–1 |
–1 |
–1 |
–1 |
+1 |
+1 |
|
|
3 |
–1 |
+1 |
–1 |
–1 |
+1 |
–1 |
+1 |
|
|
4 |
+1 |
+1 |
–1 |
+1 |
–1 |
–1 |
–1 |
|
|
5 |
–1 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
|
|
6 |
+1 |
–1 |
+1 |
–1 |
+1 |
–1 |
–1 |
|
|
7 |
–1 |
+1 |
+1 |
–1 |
–1 |
+1 |
–1 |
|
|
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
|
|
Контрасты факторов и взаимодействий находятся так же, как и в случае эксперимента :
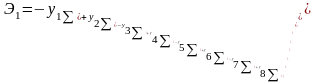






Необходимые для дисперсионного анализа суммы квадратов, соответствующие влиянию факторов и взаимодействий, определяются из уравнения
 (5.5)
(5.5)
Способ
построения матриц экспериментов типа
ясен из табл. 5.4, в которой приведены
планы полных факторных экспериментов
от
до
 .
Часто цифру 1 опускают, и матрица
планирования состоит из строк с
сочетаниями знаков (+) и (–). Фиктивная
переменная
.
Часто цифру 1 опускают, и матрица
планирования состоит из строк с
сочетаниями знаков (+) и (–). Фиктивная
переменная
 +1
введена в матрицу планирования для
единообразия записи и используется в
дальнейшем при расчете свободного члена
математической модели эксперимента.
Столбцы для парных взаимодействий и
взаимодействий более высоких порядков
получаются перемножением столбцов
соответствующих факторов. Отметим
следующие свойства таких матриц. Первое
из них – симметричность относительно
центра эксперимента: алгебраическая
сумма элементов вектор–столбца каждого
+1
введена в матрицу планирования для
единообразия записи и используется в
дальнейшем при расчете свободного члена
математической модели эксперимента.
Столбцы для парных взаимодействий и
взаимодействий более высоких порядков
получаются перемножением столбцов
соответствующих факторов. Отметим
следующие свойства таких матриц. Первое
из них – симметричность относительно
центра эксперимента: алгебраическая
сумма элементов вектор–столбца каждого
фактора
равна нулю,
 где
–
номер фактора,
где
–
номер фактора, –
номер опыта. Второе – свойство нормировки:
сумма квадратов элементов каждого
столбца равна числу опытов,
–
номер опыта. Второе – свойство нормировки:
сумма квадратов элементов каждого
столбца равна числу опытов,
 Третье свойство – ортогональность
матрицы: сумма парных произведений
элементов любых двух столбцов равна
нулю,
Третье свойство – ортогональность
матрицы: сумма парных произведений
элементов любых двух столбцов равна
нулю,
 при этом
при этом
 .
Последнее свойство – ротатабельность
матрицы: точность предсказания зависимой
переменной одинакова на равных расстояниях
от центра эксперимента и не зависит от
направления. Суммы квадратов,
.
Последнее свойство – ротатабельность
матрицы: точность предсказания зависимой
переменной одинакова на равных расстояниях
от центра эксперимента и не зависит от
направления. Суммы квадратов,
Таблица 5.4 Матрица полных факторных экспериментов от до
План эксперимента |
Номер опыта |
|
|
|
|
|
|
24
22
23
|
1 |
+ |
– |
– |
– |
– |
|
2 |
+ |
+ |
– |
– |
– |
|
|
3 |
+ |
– |
+ |
– |
– |
|
|
4 |
+ |
+ |
+ |
– |
– |
|
|
5 |
+ |
– |
– |
+ |
– |
|
|
6 |
+ |
+ |
– |
+ |
– |
|
|
7 |
+ |
– |
+ |
+ |
– |
|
|
8 |
+ |
+ |
+ |
+ |
– |
|
|
9 |
+ |
– |
– |
– |
+ |
|
|
10 |
+ |
+ |
– |
– |
+ |
|
|
11 |
+ |
– |
+ |
– |
+ |
|
|
12 |
+ |
+ |
+ |
– |
+ |
|
|
13 |
+ |
– |
– |
+ |
+ |
|
|
14 |
+ |
+ |
– |
+ |
+ |
|
|
15 |
+ |
– |
+ |
+ |
+ |
|
|
16 |
+ |
+ |
+ |
+ |
+ |
|
соответствующие влиянию факторов и взаимодействий, рассчитываются по уравнению
 (5.6)
(5.6)
где
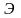 -
контраст фактора или взаимодействия,
получаемый в результате алгебраического
сложения столбца суммарных значений
отклика
-
контраст фактора или взаимодействия,
получаемый в результате алгебраического
сложения столбца суммарных значений
отклика
 со знаками соответствующего столбца
–фактора
или взаимодействия,
со знаками соответствующего столбца
–фактора
или взаимодействия,
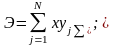 (5.7)
(5.7)
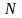 — число
опытов,
— число
опытов,
 .
.
Суммы квадратов и рассчитываются по уравнениям
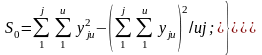 (5.8)
(5.8)
где
 – общая сумма квадратов факторов и
взаимодействий, рассчитанных по уравнению
(5.6).
– общая сумма квадратов факторов и
взаимодействий, рассчитанных по уравнению
(5.6).
Результаты дисперсионного анализа представляются в виде табл. 5.5. Отношение
 (5.9)
(5.9)
оценивает долю вариации отклика, обусловленную рассматриваемым фактором или взаимодействием.
Простейшей математической моделью полного факторного эксперимента, как известно, является линейная, описываемая уравнением
 (5.10)
(5.10)
Коэффициенты
модели определяются из системы линейных
уравнений (4.2). Поскольку суммы попарных
произведений
 при
,
системе таких уравнений соответствует
определитель
при
,
системе таких уравнений соответствует
определитель
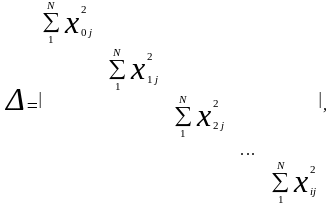 (5.11)
(5.11)
равный
 (5.12)
(5.12)
Соответственно определитель
 (5.13)
(5.13)
Тогда коэффициенты находятся из уравнений
 (5.14)
(5.14)
Учитывая,
что
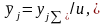 получим:
получим:
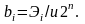 (5.15)
(5.15)
Следует
отметить, что коэффициенты
 являются взаимонезависимыми, что нельзя
утверждать в случае пассивного
эксперимента.
являются взаимонезависимыми, что нельзя
утверждать в случае пассивного
эксперимента.
После
вычисления коэффициентов
модель анализируется теми же методами,
что и уравнение множественной регрессии.
В общем случае план
позволяет оценить
 линейных эффектов и эффектов взаимодействия
(см. табл. 5.5). В связи с этим на первом
этапе следует провести дисперсионный
анализ экспериментальных данных и
выявить значимые линейные эффекты и
эффекты взаимодействий, составляющих
основу линейной модели. При отсутствии
повторений удается проверить только
значимость уравнения -модели. Линейная
модель значима, если
линейных эффектов и эффектов взаимодействия
(см. табл. 5.5). В связи с этим на первом
этапе следует провести дисперсионный
анализ экспериментальных данных и
выявить значимые линейные эффекты и
эффекты взаимодействий, составляющих
основу линейной модели. При отсутствии
повторений удается проверить только
значимость уравнения -модели. Линейная
модель значима, если
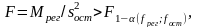 (5.16)
(5.16)
где
 сумма средних квадратов значимых
линейных эффектов и эффектов взаимодействий,
сумма средних квадратов значимых
линейных эффектов и эффектов взаимодействий,

 остаточный средний квадрат (сумма
квадратов, используемая для его
вычисления,
);
остаточный средний квадрат (сумма
квадратов, используемая для его
вычисления,
);
 ,
т. е. равно числу значимых эффектов,
число степеней свободы остаточного
среднего квадрата равно
,
т. е. равно числу значимых эффектов,
число степеней свободы остаточного
среднего квадрата равно

Средний
квадрат
иногда называют дисперсией неадекватности.
Для проверки адекватности вычисляют
дисперсию воспроизводимости для каждого
опыта с
 степенями свободы
степенями свободы
 (5.17)
(5.17)
Таблица 5.5. Результаты дисперсионного анализа эксперимента типа с повторениями
Источник изменчивости |
Число степеней свободы |
Сумма квадратов |
Средний квадрат |
- отношение |
Факторы:
…
|
|
|
…
|
…
|
Уравнение
5.6
… |
|
… |
… |
|
Взаимодействие трех факторов
… |
|
… |
… |
|
Взаимодействие четырех и более факторов … |
… |
… |
… |
|
Ошибка |
|
|
|
_ |
Сумма |
|
|
_ |
_ |
Если такие дисперсии однородны, что проверяется с помощью критерия Кохрана (см. прил. табл. 6), для дальнейших расчетов принимается среднее значение дисперсии
 (5.18)
(5.18)
с
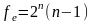 степенями свободы. Линейная модель
адекватна при
степенями свободы. Линейная модель
адекватна при
 .
(5.19)
.
(5.19)
Если модель неадекватна, необходимо перенести центр эксперимента или изменить интервалы варьирования факторов, или построить план более высокого порядка. При выявлении неоднородности дисперсий воспроизводимости в опытах следует преобразовать исходные данные (например, прологарифмировать их), чтобы дисперсии стали однородными.
Иногда опыты повторяют только в центре плана, тогда в качестве дисперсии воспроизводимости принимают
 (5.20)
(5.20)
с
 степенями свободы.
степенями свободы.
Напомним,
что линейная модель получается в
переменных, принимающих значения (+1)
или (–1). Если необходимо перейти к
натуральным переменным
 ,
нужно вместо
подставить значения натуральных
переменных
,
нужно вместо
подставить значения натуральных
переменных
 (5.21)
(5.21)
Рассмотрим метод дробных факторных экспериментов типа . Если в качестве уравнения связи между исследуемыми переменными принять линейную модель и пренебречь эффектами взаимодействий, то минимально возможное число опытов эксперимента должно быть не меньше или, в крайнем случае, равно числу коэффициентов модели.
Так, вместо восьми опытов для изучения трех факторов (как это было в случае полного факторного эксперимента ) оказывается достаточным поставить четыре, т. е. воспользоваться дробной репликой от полного факторного эксперимента. При построении дробных реплик используют следующее правило: при введении в планирование нового фактора следует этому фактору присвоить столбец матрицы, принадлежащий взаимодействию, которое можно не учитывать.
Рассмотрим вначале случай с тремя факторами. Полная матрица планирования двухфакторного эксперимента дана в табл. 5.3. Модель такого эксперимента представим как
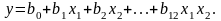 (5.22)
(5.22)
Если
пренебречь парным взаимодействием, т.
е. принять
 ,
то столбец матрицы
можно
использовать для нового фактора
.
В этом случае матрица планирования
выглядит в виде табл. 5.6.
,
то столбец матрицы
можно
использовать для нового фактора
.
В этом случае матрица планирования
выглядит в виде табл. 5.6.
Таблицы
5.6. Полуреплики плана
(планы
 )
)
|
|
|
|
|
|
|
Определяющий
контраст
|
||||||
1 |
+ |
+ |
+ |
+ |
+ |
+ |
2 |
- |
+ |
- |
- |
+ |
+ |
3 |
+ |
- |
- |
+ |
- |
+ |
4 |
- |
- |
+ |
- |
- |
+ |
Определяющий
контраст
|
||||||
1 |
+ |
+ |
- |
- |
- |
- |
2 |
- |
+ |
+ |
+ |
- |
- |
3 |
+ |
- |
- |
+ |
+ |
- |
4 |
- |
- |
- |
+ |
+ |
- |
Однако
при этом столбцы
и
,
и
,
а
также
и
одинаковы.
Значит, оценки
 и
и
 смешаны соответственно с оценками
смешаны соответственно с оценками
 и
и
 ,
что записывается следующим образом:
,
что записывается следующим образом:
 (5.23)
(5.23)
где
под
 понимается истинное значение коэффициента
регрессии.
понимается истинное значение коэффициента
регрессии.
Построение
плана
 начинают с соотношения
=
,
называемого генерирующим. При умножении
обеих частей его на
получим
начинают с соотношения
=
,
называемого генерирующим. При умножении
обеих частей его на
получим
 или, поскольку
=±1,
1=
.
Выражение этого типа называется
определяющим контрастом. С его помощью
легко установить, какие эффекты смешаны.
Для этого нужно умножить контраст на
интересующий нас фактор. Так, для
имеем
или, поскольку
=±1,
1=
.
Выражение этого типа называется
определяющим контрастом. С его помощью
легко установить, какие эффекты смешаны.
Для этого нужно умножить контраст на
интересующий нас фактор. Так, для
имеем
 ,
так как
,
так как
 .
Другим определяющим контрастом для
дробной реплики
(полуреплики) является 1=
.
Другим определяющим контрастом для
дробной реплики
(полуреплики) является 1= .
Ему соответствуют генерирующее
соотношение
=
.
Ему соответствуют генерирующее
соотношение
= и
матрица планирования (табл.5.6 ). В этом
случае запишем следующее смешивание
оценок:
и
матрица планирования (табл.5.6 ). В этом
случае запишем следующее смешивание
оценок:
 (5.24)
(5.24)
При
построении дробных реплик (полуреплик)
 возможны уже 8 решений: 1)
=
(или
=
);
2)
=
(или
=
возможны уже 8 решений: 1)
=
(или
=
);
2)
=
(или
= );
3)
=
);
3)
= (или
=
(или
=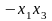 );
4)
);
4)
 (или
(или
 ).
).
Системы
смешивания оценок для каждой из таких
реплик различны. При отсутствии информации
об эффектах взаимодействия стремятся
выбрать реплику с наибольшей разрешающей
способностью, т. е. реплику, у которой
линейные эффекты смешаны с эффектами
взаимодействий наиболее высокого
порядка. Для реплик
это будут полуреплики, заданные
определяющими контрастами 1= и 1=
и 1= .
Система смешивания оценок для таких
реплик
.
Система смешивания оценок для таких
реплик
 (5.25)
(5.25)
где знак “ + ” соответствует первому контрасту, а знак “–” – второму.
При
выборе полуреплик
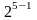 возможны
уже 22 варианта. Варианты, для которых
возможны
уже 22 варианта. Варианты, для которых
 =
и
=
и
 =
,
соответствуют репликам с наибольшей
разрешающей способностью. При исследовании
влияния пяти факторов можно еще больше
уменьшить число опытов – поставить не
16 опытов (как при плане
),
а только 8, т. е. воспользоваться четверть
репликой
=
,
соответствуют репликам с наибольшей
разрешающей способностью. При исследовании
влияния пяти факторов можно еще больше
уменьшить число опытов – поставить не
16 опытов (как при плане
),
а только 8, т. е. воспользоваться четверть
репликой .
В этом случае возможны 12 вариантов, если
приравнять к парному взаимодействию,
а
– тройному. Если выбран вариант, когда
=
и
=
,
то определяющими контрастами являются
1=
.
В этом случае возможны 12 вариантов, если
приравнять к парному взаимодействию,
а
– тройному. Если выбран вариант, когда
=
и
=
,
то определяющими контрастами являются
1= и 1=
и 1= .
При перемножении этих контрастов
получается третье соотношение 1=
.
При перемножении этих контрастов
получается третье соотношение 1= .
Разрешаемую
способность такой реплики определяет
обобщающий контраст 1=
=
=
.
Систему смешивания оценок получают
умножением обобщающего контраста
последовательно на
.
Разрешаемую
способность такой реплики определяет
обобщающий контраст 1=
=
=
.
Систему смешивания оценок получают
умножением обобщающего контраста
последовательно на
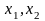 и
т. д.:
и
т. д.:
 (5.26)
(5.26)
Получается довольно сложная система смешивания эффектов с эффектами взаимодействия первого, второго, третьего и четвертого порядков. Чтобы нивелировать значимость парных взаимодействий, следует поставить вторую серию опытов, воспользовавшись так называемым методом “перевала”. Смысл этого метода заключается в том, что вторая четвертьреплика получается из первой путем изменения всех знаков матрицы на обратные. Тогда в обобщающем контрасте реплики тройные взаимодействия (определяющие парные взаимодействия в системе смешивания оценок) будут иметь знак, противоположный их знаку в первой четвертьреплике. Усредняя результаты обеих четвертьреплик, получаем эффекты, не смешанные с парными взаимодействиями.
Таблица П1. Фрагмент таблицы случайных чисел [1]
56 |
66 |
25 |
32 |
38 |
64 |
70 |
26 |
27 |
67 |
77 |
40 |
04 |
34 |
63 |
98 |
99 |
89 |
31 |
16 |
12 |
90 |
50 |
28 |
96 |
88 |
40 |
52 |
02 |
29 |
82 |
69 |
34 |
50 |
21 |
74 |
00 |
91 |
27 |
52 |
98 |
72 |
03 |
45 |
65 |
30 |
89 |
71 |
45 |
91 |
87 |
63 |
88 |
23 |
62 |
51 |
07 |
69 |
59 |
02 |
89 |
49 |
14 |
98 |
53 |
41 |
92 |
36 |
07 |
76 |
85 |
37 |
84 |
37 |
47 |
32 |
25 |
21 |
15 |
08 |
82 |
34 |
57 |
57 |
35 |
22 |
03 |
33 |
48 |
84 |
37 |
37 |
29 |
38 |
37 |
89 |
76 |
25 |
09 |
69 |
44 |
61 |
88 |
23 |
13 |
01 |
59 |
47 |
64 |
04 |
99 |
59 |
96 |
20 |
30 |
87 |
31 |
33 |
69 |
45 |
58 |
48 |
00 |
83 |
48 |
94 |
44 |
08 |
67 |
79 |
41 |
61 |
41 |
15 |
60 |
11 |
88 |
83 |
24 |
82 |
24 |
07 |
78 |
61 |
89 |
42 |
58 |
88 |
22 |
16 |
13 |
24 |
40 |
09 |
00 |
65 |
46 |
38 |
61 |
12 |
90 |
62 |
41 |
11 |
59 |
85 |
18 |
42 |
61 |
29 |
88 |
76 |
04 |
21 |
80 |
78 |
27 |
84 |
05 |
99 |
85 |
75 |
67 |
80 |
05 |
57 |
05 |
71 |
70 |
31 |
31 |
99 |
99 |
06 |
96 |
53 |
99 |
25 |
13 |
63 |
42 |
39 |
30 |
02 |
34 |
99 |
46 |
64 |
45 |
15 |
19 |
74 |
15 |
50 |
17 |
44 |
80 |
13 |
86 |
38 |
40 |
45 |
82 |
13 |
44 |
04 |
52 |
43 |
96 |
38 |
13 |
83 |
80 |
72 |
34 |
20 |
84 |
56 |
19 |
49 |
59 |
14 |
85 |
42 |
99 |
71 |
16 |
34 |
33 |
79 |
82 |
85 |
77 |
30 |
16 |
69 |
32 |
46 |
46 |
30 |
84 |
20 |
68 |
72 |
98 |
94 |
62 |
63 |
59 |
44 |
00 |
89 |
06 |
15 |
87 |
38 |
48 |
84 |
88 |
24 |
55 |
46 |
48 |
60 |
06 |
90 |
08 |
83 |
83 |
98 |
40 |
90 |
88 |
25 |
26 |
85 |
74 |
55 |
80 |
85 |
91 |
19 |
05 |
68 |
22 |
58 |
04 |
63 |
21 |
16 |
23 |
38 |
25 |
43 |
32 |
98 |
94 |
65 |
35 |
35 |
16 |
91 |
07 |
12 |
43 |
54 |
81 |
87 |
21 |
31 |
40 |
46 |
17 |
62 |
63 |
99 |
71 |
14 |
12 |
64 |
51 |
68 |
50 |
60 |
78 |
22 |
69 |
51 |
97 |
37 |
65 |
43 |
75 |
12 |
91 |
20 |
36 |
25 |
57 |
92 |
33 |
65 |
95 |
48 |
75 |
00 |
06 |
65 |
25 |
90 |
16 |
29 |
34 |
14 |
43 |
49 |
98 |
71 |
31 |
80 |
59 |
57 |
32 |
43 |
07 |
85 |
06 |
64 |
75 |
27 |
29 |
17 |
06 |
11 |
30 |
68 |
70 |
97 |
87 |
21 |
03 |
98 |
68 |
89 |
39 |
71 |
87 |
32 |
14 |
99 |
42 |
10 |
25 |
37 |
30 |
08 |
27 |
75 |
43 |
97 |
54 |
20 |
69 |
93 |
50 |
56 |
04 |
21 |
34 |
92 |
89 |
81 |
52 |
15 |
12 |
84 |
11 |
12 |
66 |
87 |
48 |
21 |
06 |
86 |
08 |
35 |
39 |
52 |
28 |
09 |
48 |
09 |
36 |
95 |
36 |
20 |
82 |
53 |
32 |
89 |
92 |
68 |
50 |
88 |
17 |
37 |
92 |
02 |
23 |
43 |
63 |
24 |
69 |
80 |
91 |
23 |
97 |
10 |
96 |
57 |
74 |
07 |
95 |
26 |
44 |
93 |
08 |
43 |
30 |
41 |
86 |
45 |
74 |
33 |
78 |
84 |
33 |
38 |
76 |
73 |
43 |
97 |
55 |
45 |
98 |
35 |
69 |
45 |
96 |
80 |
46 |
26 |
39 |
96 |
33 |
60 |
20 |
73 |
30 |
79 |
17 |
19 |
03 |
47 |
28 |
40 |
05 |
08 |
50 |
79 |
89 |
57 |
19 |
86 |
48 |
27 |
98 |
99 |
24 |
08 |
94 |
19 |
15 |
81 |
29 |
82 |
14 |
35 |
88 |
03 |
66 |
97 |
10 |
69 |
02 |
25 |
36 |
43 |
71 |
76 |
00 |
67 |
56 |
12 |
69 |
07 |
89 |
55 |
63 |
31 |
50 |
72 |
20 |
33 |
36 |
15 |
62 |
38 |
72 |
92 |
03 |
76 |
09 |
30 |
75 |
77 |
80 |
04 |
24 |
54 |
67 |
60 |
10 |
79 |
26 |
21 |
60 |
03 |
48 |
14 |
77 |
81 |
15 |
14 |
67 |
55 |
24 |
22 |
20 |
55 |
36 |
93 |
67 |
68 |
37 |
72 |
22 |
43 |
46 |
32 |
56 |
15 |
75 |
25 |
12 |
18 |
87 |
05 |
09 |
96 |
45 |
14 |
72 |
41 |
46 |
12 |
67 |
46 |
72 |
02 |
59 |
06 |
17 |
49 |
12 |
73 |
28 |
23 |
52 |
48 |
08 |
58 |
53 |
63 |
66 |
13 |
70 |
04 |
48 |
71 |
39 |
07 |
46 |
96 |
40 |
20 |
86 |
79 |
11 |
81 |
74 |
11 |
15 |
23 |
17 |
16 |
07 |
79 |
57 |
61 |
42 |
19 |
68 |
15 |
12 |
60 |
21 |
59 |
12 |
07 |
04 |
99 |
88 |
22 |
39 |
75 |
16 |
69 |
13 |
84 |
Таблица 1. Квантили распределения Стьюдента [101]
|
f |
|
f |
|
||||||||
|
0,05 |
0,01 |
0,05 |
0,01 |
||||||||
1 |
12,71 |
63,66 |
18 |
2,10 |
2,88 |
|
||||||
2 |
4,30 |
9,92 |
19 |
2,09 |
2,86 |
|
||||||
3 |
3,18 |
5,84 |
20 |
2,09 |
2,84 |
|
||||||
4 |
2,78 |
4,60 |
21 |
2,08 |
2,83 |
|
||||||
5 |
2,57 |
4,03 |
22 |
2,07 |
2,82 |
|
||||||
6 |
2,45 |
3,71 |
23 |
2,07 |
2,81 |
|
||||||
7 |
2,36 |
3,50 |
24 |
2,06 |
2,80 |
|
||||||
8 |
2,31 |
3,36 |
25 |
2,06 |
2,79 |
|
||||||
9 |
2,26 |
3,25 |
26 |
2,06 |
2,78 |
|
||||||
10 |
2,23 |
3,17 |
27 |
2,05 |
2,77 |
|
||||||
11 |
2,20 |
3,11 |
28 |
2,05 |
2,76 |
|
||||||
12 |
2,18 |
3,06 |
29 |
2,04 |
2,76 |
|
||||||
13 |
2,16 |
3,01 |
30 |
2,04 |
2,75 |
|
||||||
14 |
2,14 |
2,98 |
40 |
2,02 |
2,70 |
|
||||||
15 |
2,13 |
2,95 |
60 |
2,00 |
2,66 |
|
||||||
16 |
2,12 |
2,92 |
120 |
1,98 |
2,62 |
|
||||||
17 |
2,11 |
2,90 |
|
1,96 |
2,58 |
|
||||||
Таблица 3. Квантили распределения Пирсона [75]
f |
|
|
||
|
||||
0,05 |
0,02 |
0,05 |
0,02 |
|
2 |
7,38 |
9,21 |
0,051 |
0,020 |
3 |
9,35 |
11,34 |
0,216 |
0,115 |
4 |
11,14 |
13,28 |
0,484 |
0,297 |
5 |
12,83 |
15,08 |
0,831 |
0,554 |
6 |
14,45 |
16,81 |
1,24 |
0,872 |
7 |
16,01 |
18,48 |
1,692 |
1,24 |
8 |
17,53 |
20,09 |
2,18 |
1,65 |
9 |
19,01 |
21,67 |
2,70 |
2,09 |
10 |
20,48 |
23,21 |
3,25 |
2,56 |
11 |
21,92 |
24,72 |
3,82 |
3,05 |
12 |
23,34 |
26.22 |
4,40 |
3,57 |
13 |
24,74 |
27,69 |
5,01 |
4,11 |
14 |
26,12 |
29,14 |
5,63 |
4,66 |
15 |
27,49 |
30,58 |
6,26 |
5,23 |
16 |
28,85 |
32,00 |
6,91 |
5,81 |
17 |
30,19 |
33,41 |
7,56 |
6,41 |
18 |
31,53 |
34,81 |
8,23 |
7,01 |
19 |
32,85 |
36,19 |
8,91 |
7,63 |
20 |
34,17 |
37,57 |
9,59 |
8,26 |
22 |
36,78 |
40,29 |
10,98 |
9,54 |
24 |
39,36 |
42,98 |
12,40 |
10,86 |
26 |
41,92 |
45,64 |
13,84 |
12,20 |
27 |
44,46 |
48,28 |
15,31 |
13,56 |
30 |
46,98 |
50,89 |
16,79 |
14,95 |
35 |
53,20 |
57,34 |
20,57 |
18,51 |
40 |
59,34 |
63,69 |
24,43 |
22,16 |
45 |
65,41 |
69,96 |
28,37 |
25,90 |
50 |
71,42 |
76,15 |
32,36 |
29,71 |
60 |
83,30 |
88,38 |
40,48 |
37,48 |
70 |
95,02 |
100,43 |
48,76 |
45,44 |
80 |
106,63 |
112,33 |
57,15 |
53,54 |
90 |
118,14 |
124,12 |
65,65 |
61,75 |
100 |
129,56 |
135,81 |
74,22 |
70,06 |
Таблица
5. Квантили
распределения
 [101]
[101]
Число степеней свободы для знамена-теля f2 |
|
Число степеней свободы для числителя f |
|||||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
15 |
20 |
30 |
40 |
60 |
120 |
|
||
1 |
0.05 |
161 |
200 |
216 |
225 |
2.30 |
234 |
237 |
239 |
241 |
242 |
243 |
246 |
248 |
250 |
251 |
252 |
253 |
254 |
2 |
0,05 |
18,5 |
19,0 |
19,2 |
19,2 |
19,3 |
19,3 |
19,4 |
19,4 |
19,4 |
19.4 |
19,4 |
19,4 |
19,4 |
19,5 |
19,5 |
19,5 |
19,5 |
19,5 |
|
0,01 |
98,5 |
99,0 |
99,2 |
99,2 |
99,3 |
99,3 |
99.4 |
99,4 |
99,4 |
99,4 |
99,4 |
99,4 |
99,4 |
99,5 |
99,5 |
99,5 |
99,5 |
99,5 |
3 |
0,05 |
10,1 |
9.55 |
9,28 |
9,12 |
9,10 |
8,94 |
8,89 |
8.85 |
8.81 |
8.79 |
8,76 |
8,70 |
8,66 |
8,62 |
8,59 |
8,57 |
8,55 |
8,53 |
|
0,01 |
34,1 |
30.8 |
29,5 |
28,7 |
28,2 |
27,9 |
27.7 |
27,5 |
27,3 |
27,2 |
27,1 |
26,9 |
26,7 |
26,5 |
26,4 |
26,3 |
26,2 |
26,1 |
4 |
0,05 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
6,00 |
5,96 |
5,94 |
5,86 |
5,80 |
5,75 |
5,72 |
5,69 |
5,66 |
5,63 |
|
0,01 |
21,1 |
18,0 |
16,7 |
16.0 |
15,5 |
15,2 |
15,0 |
14,8 |
14,7 |
14.5 |
14,4 |
14,2 |
14,0 |
14,0 |
13,7 |
13,7 |
13,6 |
13,5 |
5 |
0,05 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,85 |
4,88 |
4,82 |
4,77 |
4,74 |
4.71 |
4,62 |
4,56 |
4,50 |
4,46 |
4,43 |
4,40 |
4,36 |
|
0,01 |
16,3 |
13,3 |
12,1 |
11,4 |
11,0 |
10,7 |
10,5 |
10,3 |
10,2 |
10.1 |
9,96 |
9,72 |
9,55 |
9,38 |
9,29 |
9,20 |
9,11 |
9,02 |
6 |
0,05 |
5,99 |
5.14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4.10 |
4,06 |
4,03 |
3,94 |
3,87 |
3,81 |
3,77 |
3,74 |
3,70 |
3,67 |
|
0.01 |
13.7 |
10,9 |
9.78 |
9,15 |
8,75 |
8.47 |
8.26 |
8,10 |
7,98 |
7,87 |
7,79 |
7,56 |
7,40 |
7,23 |
7,14 |
7,06 |
6,97 |
6,88 |
7 |
0,05 |
5,59 |
4,74 |
4.35 |
4,12 |
3,97 |
3.87 |
3,79 |
3.73 |
3.68 |
3,64 |
3,60 |
3.51 |
3,44 |
3,38 |
3,34 |
3,30 |
3,27 |
3,23 |
|
0.01 |
12,2 |
9,55 |
8,45 |
7,85 |
7,46 |
7.19 |
6.99 |
6,84 |
6,72 |
6.62 |
6,54 |
6,31 |
6,16 |
5,99 |
5,91 |
5,82 |
5,74 |
5,65 |
8 |
0,05 |
5,32 |
4,46 |
4,07 |
3.84 |
3,69 |
3.58 |
3,50 |
3,44 |
3.39 |
3,35 |
3.31 |
3,22 |
3,15 |
3,08 |
3,04 |
3,01 |
2,97 |
2,93 |
|
0,01 |
11,3 |
8,65 |
7,59 |
7.01 |
6,63 |
6,37 |
6,18 |
6,03 |
5,91 |
5,81 |
5.73 |
5,52 |
5,36 |
5,20 |
5,12 |
5,03 |
4,95 |
4,86 |
9 |
0,05 |
5,12 |
4.26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3.23 |
3.18 |
3,14 |
3,10 |
3,03 |
2,94 |
2,86 |
2,83 |
2,79 |
2,75 |
2,71 |
|
0,01 |
10,1 |
8,02 |
6,99 |
6,42 |
6,06 |
5.80 |
5,61 |
5,47 |
5.35 |
5,26 |
5,18 |
4,96 |
4,81 |
4,65 |
4,57 |
4,48 |
4,40 |
4,31 |
10 |
0.05 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3.07 |
3,02 |
2,98 |
2.94 |
2,85 |
2,77 |
2,70 |
2,66 |
2,62 |
2,58 |
2,54 |
|
0.01 |
10,0 |
7.56 |
6,55 |
5,99 |
5,64 |
5.39 |
5,20 |
5,06 |
4.94 |
4,85 |
4,77 |
4,56 |
4,41 |
4,25 |
4,17 |
4,08 |
4,00 |
3,91 |
11 |
0.05 |
4,84 |
3,98 |
3.59 |
3.36 |
3.20 |
3,09 |
3,01 |
2.95 |
2,90 |
2,85 |
2,82 |
2,72 |
2,65 |
2,57 |
2,53 |
2,49 |
2,45 |
2,40 |
|
0.01 |
9,65 |
7.21 |
6.22 |
5,67 |
5,32 |
5,07 |
4.89 |
4,74 |
4,63 |
4,54 |
4,46 |
4,25 |
4,10 |
3,94 |
3,86 |
3,78 |
3,69 |
3,60 |
12 |
0,05 |
4,75 |
3,89 |
3,49 |
3,26 |
3.11 |
3,00 |
2,91 |
2.85 |
2,80 |
2.75 |
2,72 |
2,62 |
2,54 |
2,47 |
2,43 |
,38 |
2,34 |
2,30 |
|
0.01 |
9,33 |
6,93 |
5,95 |
5,41 |
5.06 |
4,82 |
4,64 |
4.50 |
4.39 |
4,30 |
4,22 |
4,01 |
3,86 |
3,70 |
3,2 |
3,54 |
3,45 |
3,36 |
13 |
0,05 |
4,67 |
3.81 |
3,41 |
3,18 |
3,03 |
2,92 |
2,83 |
2.77 |
2,71 |
2,67 |
2,63 |
2.53 |
2,46 |
2,38 |
2,34 |
2,30 |
2,25 |
2,21 |
|
0.01 |
9,07 |
6,70 |
5,74 |
5,21 |
4,86 |
4,62 |
4.44 |
4,30 |
4,19 |
4,10 |
4.02 |
3,82 |
3,66 |
3,51 |
3,43 |
3,34 |
3,25 |
3,17 |
14 |
0,05 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,76 |
2.70 |
2,65 |
2,60 |
2.57 |
2,46 |
2,39 |
2,31 |
2,27 |
2,22 |
2,18 |
2,13 |
|
0.01 |
8,86 |
6,51 |
5,56 |
5,04 |
4,69 |
4,46 |
4,28 |
4,14 |
4.03 |
3.94 |
3,86 |
3,66 |
3,51 |
3,35 |
3,27 |
3,18 |
3,09 |
3,00 |
окончание табл. .5 |
|||||||||||||||||||
15 |
0,05 |
4.54 |
3,68 |
3,29 |
3.06 |
2,90 |
2.79 |
2.71 |
2,64 |
2,59 |
2,54 |
2,51 |
2,40 |
2,33 |
2,25 |
2,20 |
2,16 |
2,11 |
2,07 |
|
0,01 |
8.68 |
6,36 |
5.42 |
4,89 |
4.56 |
4,32 |
4.14 |
4.00 |
3.89 |
3,80 |
3,73 |
3,52 |
3,33 |
3,21 |
3,13 |
3,05 |
2,96 |
2,87 |
16 |
0,05 |
4,49 |
3.63 |
3,24 |
3,01 |
2.85 |
2,74 |
2,66 |
2,59 |
2.54 |
2.49 |
2,46 |
2,35 |
2,28 |
2,19 |
2,15 |
2,11 |
2,06 |
2,01 |
|
0,01 |
8,53 |
6,23 |
5.29 |
4.77 |
4,44 |
4,20 |
4,03 |
3.89 |
3,78 |
3,69 |
3,62 |
3.41 |
3,26 |
3,10 |
3,02 |
2,93 |
2,84 |
2,75 |
17 |
0,05 |
4,45 |
3.59 |
3.20 |
2.96 |
2.81 |
2,70 |
2.61 |
2,55 |
2.49 |
2,45 |
2,41 |
2,31 |
2,23 |
2,15 |
2,10 |
2,06 |
2,01 |
1,96 |
|
0,01 |
8,40 |
6,11 |
5,18 |
4.67 |
4,34 |
4.10 |
3,93 |
3,79 |
З,68 |
3.59 |
3,52 |
3.31 |
3,16 |
3,00 |
2,92 |
2,83 |
2,75 |
2,65 |
18 |
0,05 |
4,41 |
3.55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,58 |
2,51 |
2,46 |
2,41 |
2,37 |
2,27 |
2,19 |
2,11 |
2,06 |
2,02 |
1,97 |
1,92 |
|
0,01 |
8,29 |
6,01 |
5,09 |
4.58 |
4,25 |
4,01 |
3,84 |
3,71 |
3,60 |
3.51 |
З,43 |
3.23 |
3,08 |
2,92 |
2,84 |
2,75 |
2,66 |
2,57 |
19 |
0.05 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2.63 |
2.54 |
2,48 |
2.42 |
2,38 |
2,34 |
2,23 |
2,16 |
2,07 |
2,03 |
1,98 |
1,93 |
1,88 |
|
0.01 |
8.18 |
5.93 |
5,01 |
4,50 |
4,17 |
3,94 |
3.77 |
3.63 |
3,52 |
3,43 |
3,36 |
3,15 |
3,00 |
2,84 |
2,76 |
2,67 |
2,58 |
2,49 |
20 |
0.05 |
4,35 |
3.49 |
3,10 |
2,87 |
2.71 |
2,60 |
2.51 |
2,45 |
2,39 |
2,35 |
2,31 |
2.20 |
2,12 |
2,04 |
1,99 |
1,95 |
1,90 |
1,84 |
|
0,01 |
8,10 |
5.85 |
4.94 |
4,43 |
4.10 |
3,87 |
3,70 |
3,56 |
3,46 |
3,37 |
3.29 |
3,09 |
2.94 |
2,78 |
2,69 |
2,61 |
2,52 |
2,42 |
22 |
0.05 |
4,30 |
3,44 |
3.05 |
2,82 |
2,66 |
2,55 |
2,46 |
2,40 |
2,34 |
2,30 |
2.26 |
2,15 |
2,07 |
1,98 |
1,94 |
1,89 |
1,84 |
1,78 |
|
0,01 |
7.95 |
5,72 |
4,82 |
4.31 |
3.99 |
3,76 |
3,59 |
3,45 |
3,35 |
3,26 |
3,18 |
2,98 |
2.83 |
2,67 |
2,58 |
2,50 |
2,40 |
2,31 |
24 |
0,05 |
4.26 |
3,40 |
3,01 |
2.78 |
2.62 |
2.51 |
2.42 |
2.36 |
2,30 |
2.25 |
2.21 |
2,11 |
2.03 |
1,97 |
1,89 |
1,84 |
1,79 |
1,73 |
|
0,01 |
7,82 |
5,61 |
4,72 |
4,22 |
3,90 |
3,67 |
3,50 |
3,36 |
3,26 |
3.17 |
3,09 |
2.89 |
2,74 |
2,58 |
2,49 |
2,40 |
2,31 |
2,21 |
26 |
0,05 |
4,23 |
3.37 |
2,98 |
2,74 |
2,59 |
2,47 |
2.39 |
2,32 |
2,27 |
2,22 |
2,18 |
2.07 |
1,99 |
1,90 |
1,85 |
1,80 |
1,75 |
1,69 |
|
0,01 |
7,72 |
5.53 |
4.64 |
4,14 |
3,82 |
3,59 |
3,42 |
3.29 |
3.18 |
3,09 |
3,02 |
2,81 |
2,66 |
2,50 |
2,42 |
2,33 |
2,23 |
2,13 |
28 |
0,05 |
4,20 |
3,34 |
2,95 |
2.71 |
2,56 |
2,45 |
2.36 |
2.29 |
2.24 |
2.19 |
2,15 |
2,04 |
1,96 |
1,87 |
1,82 |
1,77 |
1,71 |
1,65 |
|
0,01 |
7,64 |
5,45 |
4,57 |
4.07 |
3,75 |
3,00 |
3.36 |
3,23 |
3,12 |
3,03 |
2,96 |
2.75 |
2,60 |
2,44 |
2,35 |
2,26 |
2,17 |
2,06 |
30 |
0,05 |
4.17 |
3.32 |
2,92 |
2.69 |
2,53 |
2,42 |
2,33 |
2,27 |
2.21 |
2.16 |
2,13 |
2,01 |
1,93 |
1,84 |
1,79 |
1,74 |
1,68 |
1,62 |
|
0,01 |
7,56 |
5,39 |
4.51 |
4,02 |
3,70 |
3,47 |
3,30 |
3,17 |
3.07 |
2.98 |
2,91 |
2,70 |
2,55 |
2,39 |
2,30 |
2,21 |
2,11 |
2,01 |
40 |
0.05 |
4,08 |
323 |
2,84 |
2,61 |
2,45 |
2.34 |
2.25 |
2,18 |
2.12 |
2,08 |
2,04 |
1,92 |
1,84 |
1,74 |
1,69 |
1,64 |
1,58 |
1,51 |
|
0.01 |
7.31 |
5,18 |
4.31 |
3,83 |
3,51 |
3,29 |
3,12 |
2,99 |
2,89 |
2,80 |
2.73 |
2,52 |
2,37 |
2,20 |
2,11 |
2,02 |
1,92 |
1,80 |
60 |
0.05 |
4.00 |
3.15 |
2.76 |
2,53 |
2,37 |
2,25 |
2,17 |
2,10 |
2,04 |
1,99 |
1.95 |
1,84 |
1,75 |
1,65 |
1,59 |
1,53 |
1,47 |
1,39 |
|
0,01 |
7.08 |
4,98 |
4,13 |
3,65 |
3,34 |
3,12 |
2.95 |
2,82 |
2,72 |
2,63 |
2.56 |
2,35 |
2,20 |
2,03 |
1,94 |
1,84 |
1,73 |
1,60 |
120 |
0.05 |
3,92 |
3,07 |
2,68 |
2.45 |
2,29 |
2.17 |
2,09 |
2,02 |
1,96 |
1.91 |
1,87 |
1,75 |
1,66 |
1,55 |
1,50 |
1,45 |
1,35 |
1,25 |
|
0,01 |
6,85 |
4.79 |
3.95 |
3,48 |
3,17 |
2.96 |
2,79 |
2.66 |
2,56 |
2,47 |
2,40 |
2,19 |
2,03 |
1,86 |
1,76 |
1,66 |
1,53 |
1,38 |
200 |
0,05 |
3.89 |
3.04 |
2.65 |
2,42 |
2,26 |
2,14 |
2.06 |
1.98 |
1,93 |
1.88 |
1.84 |
1.72 |
1,62 |
1,52 |
1,46 |
1,39 |
1,29 |
1,19 |
|
0.01 |
6,76 |
4,71 |
3.88 |
3,41 |
3,11 |
2,89 |
2,73 |
2.60 |
2,50 |
2,41 |
2,34 |
2.13 |
1,97 |
1,79 |
1,69 |
1,58 |
1,44 |
1,28 |
|
0,05 |
3,84 |
3,00 |
2,60 |
2,37 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1.79 |
1,67 |
1,57 |
1,46 |
1,39 |
1,32 |
1,22 |
1,00 |
|
0.01 |
6.63 |
4,61 |
3.78 |
3,32 |
3,02 |
2.80 |
2,64 |
2.51 |
2,41 |
2,32 |
2,25 |
2,04 |
1,88 |
1,70 |
1,59 |
1,47 |
1,32 |
1,00 |
Таблица
6. Квантили
распределения Кохрана
 [75]
[75]
k |
|
f |
||||||||
1 |
2 |
3 |
4 |
5 |
8 |
10 |
36 |
|
||
2 |
0,05 |
0,99 |
0,97 |
0,94 |
0,90 |
0,88 |
0,81 |
0,79 |
0,66 |
0,50 |
0,01 |
0,99 |
0,99 |
0,98 |
0,96 |
0,94 |
0,88 |
0,85 |
0,71 |
0,50 |
|
3 |
0,05 |
0,97 |
0,87 |
0,80 |
0,74 |
0,71 |
0,63 |
0,60 |
0,47 |
0,33 |
0,01 |
0,99 |
0,94 |
0,88 |
0,83 |
0,79 |
0,71 |
0,67 |
0,51 |
0,33 |
|
4 |
0,05 |
0,91 |
0,77 |
0,68 |
0,63 |
0,59 |
0,52 |
0,49 |
0,37 |
0,25 |
0,01 |
0,97 |
0,86 |
0,78 |
0,72 |
0,68 |
0,59 |
0,55 |
0,40 |
0,25 |
|
5 |
0,05 |
0,84 |
0,68 |
0,60 |
0,54 |
0,51 |
0,44 |
0,41 |
0,31 |
0,20 |
0,01 |
0,93 |
0,79 |
0,69 |
0,63 |
0,59 |
0,50 |
0,47 |
0,33 |
0,20 |
|
6 |
0,05 |
0,78 |
0,62 |
0,53 |
0,48 |
0,44 |
0,38 |
0,36 |
0,26 |
0,17 |
0,01 |
0,88 |
0,72 |
0,62 |
0,56 |
0,52 |
0,44 |
0,41 |
0,28 |
0,17 |
|
7 |
0,05 |
0,73 |
0,56 |
0,48 |
0,43 |
0,40 |
0,34 |
0,31 |
0,23 |
0,14 |
0,01 |
0,84 |
0,66 |
0,57 |
0,51 |
0,46 |
0,39 |
0,36 |
0,25 |
0,14 |
|
8 |
0,05 |
0,68 |
0,51 |
0,44 |
0,39 |
0,36 |
0,30 |
0,28 |
0,20 |
0,12 |
0,01 |
0,79 |
0,61 |
0,52 |
0,46 |
0,42 |
0,35 |
0,32 |
0,22 |
0,12 |
|
9 |
0,05 |
0,64 |
0,48 |
0,40 |
0,36 |
0,33 |
0,28 |
0,26 |
0,18 |
0,11 |
0,01 |
0,75 |
0,57 |
0,48 |
0,42 |
0,39 |
0,32 |
0,29 |
0,20 |
0,11 |
|
10 |
0,05 |
0,60 |
0,44 |
0,37 |
0,33 |
0,30 |
0,25 |
0,23 |
0,16 |
0,10 |
0,01 |
0,72 |
0,53 |
0,45 |
39 |
0,36 |
0,29 |
0,27 |
0,18 |
0,10 |
|
20 |
0,05 |
0,39 |
0,27 |
0,22 |
0,19 |
0,17 |
0,14 |
0,13 |
0,09 |
0,05 |
0,01 |
0,48 |
0,33 |
0,26 |
0,23 |
0,20 |
0,16 |
0,15 |
0,10 |
0,05 |
|
40 |
0,05 |
0,24 |
0,16 |
0,12 |
0,11 |
0,10 |
0,08 |
0,07 |
0,05 |
0,02 |
0,01 |
0,29 |
0,19 |
0,15 |
0,13 |
0,11 |
0,09 |
0,08 |
0,05 |
0,02 |
|
60 |
0,05 |
0,17 |
0,11 |
0,09 |
0,08 |
0,07 |
0,05 |
0,05 |
0,03 |
0,02 |
0,01 |
0,21 |
0,14 |
0,11 |
0,09 |
0,08 |
0,06 |
0,06 |
0,03 |
0,02 |
|
|
0,05 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,01 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
Таблица
8. Квантили
распределения выборочного коэффициента
корреляции
 [75]
[75]
F |
|
f |
|
|||
0,05 |
0,01 |
0,05 |
0,01 |
|||
1 |
0,997 |
1,000 |
16 |
0,468 |
0,590 |
|
2 |
0,950 |
0,990 |
17 |
0,456 |
0,575 |
|
3 |
0,878 |
0,959 |
18 |
0,444 |
0,661 |
|
4 |
0,811 |
0,917 |
19 |
0,443 |
0,549 |
|
5 |
0,754 |
0,874 |
20 |
0,423 |
0,537 |
|
6 |
0,707 |
0,834 |
25 |
0,381 |
0,487 |
|
7 |
0,666 |
0,798 |
30 |
0,349 |
0,449 |
|
8 |
0,632 |
0,765 |
35 |
0,325 |
0,418 |
|
9 |
0,602 |
0.735 |
40 |
0,304 |
0,393 |
|
10 |
0,576 |
0,708 |
45 |
0.287 |
0,372 |
|
11 |
0,553 |
0,684 |
50 |
0,273 |
0,354 |
|
12 |
0,532 |
0,661 |
60 |
0.250 |
0.325 |
|
13 |
0,514 |
0,641 |
70 |
0,232 |
0,302 |
|
14 |
0,497 |
0,623 |
80 |
0,217 |
0,283 |
|
15 |
0,482 |
0,606 |
90 |
0,205 |
0,267 |
|
|
|
|
100 |
0,197 |
0,254 |
|































































 Уравнение
5.8
Уравнение
5.8

 Уравнение
5.8
Уравнение
5.8
 (
(
 )
) (
(
 )
)

