
Глава 2
2. Исследование связи между параметрами качества поверхностного слоя
В технологических исследованиях приходится определять различного рода характеристики, например показатели качества поверхностного слоя деталей. Истинные значения таких показателей можно получить при исследовании всех изготовляемых деталей. Это, безусловно, потребует больших затрат времени, поскольку число таких деталей может быть сколь угодно большим, а в ряде случаев просто невозможно. Поэтому речь может идти только о так называемых вероятностных оценках подобных показателей.
2.1. Применение методов теории выборок
Предположим,
имеется некоторая большая конечная или
бесконечная совокупность объектов
исследования, называемая генеральной.
Из нее извлекаются (с возвратом или без
возврата) объекты, образующие выборку.
Эти объекты изучаются для определения
свойств, характеристик всей генеральной
совокупности. Число

 называют объемом выборки, а характеристики,
определенные по
объектам,
– выборочными.
называют объемом выборки, а характеристики,
определенные по
объектам,
– выборочными.
На
практике чаще всего определяют выборочное
среднее
 исследуемых случайных величин
исследуемых случайных величин

 (2.1)
(2.1)
и выборочную дисперсию
 (2.2)
(2.2)
Знаменатель
дисперсии
 называют числом ее степеней свободы.
называют числом ее степеней свободы.
На основании выборочных характеристик судят о генеральных характеристиках, в частности о генеральном среднем исследуемых случайных величин и генеральной дисперсии 2.
В технологических исследованиях наряду с контролируемыми управляемыми факторами (например, режимы обработки) действуют также неуправляемые факторы (неоднородность структуры и твердости обрабатываемых поверхностей и т.п.). Чтобы нивелировать влияние таких случайных факторов на характеристики выборки, отбор ее объектов должен быть рандомизирован, т. е. проведен случайным образом.
Если объем генеральной совокупности велик, а выборка представляет лишь небольшую ее часть, результаты оценки генерального среднего и генеральной дисперсии по случайной выборке с возвратом и без возврата мало отличаются между собой.
Зная
объем выборки
,
находим с доверительной вероятностью
 следующую интервальную оценку для
генерального среднего:
следующую интервальную оценку для
генерального среднего:
 (2.3)
(2.3)
где
 – квантили распределения Стьюдента
(табл. П 1),
– квантили распределения Стьюдента
(табл. П 1),
 - среднее квадратичное отклонение.
Верхние и нижние границы отклонений
образуют так называемый доверительный
интервал. Значение ,
выраженное в процентах, показывает, в
скольких выборках из 100 такие доверительные
интервалы не будут содержать генеральное
среднее.
- среднее квадратичное отклонение.
Верхние и нижние границы отклонений
образуют так называемый доверительный
интервал. Значение ,
выраженное в процентах, показывает, в
скольких выборках из 100 такие доверительные
интервалы не будут содержать генеральное
среднее.
Относительная ошибка в определении выборочного среднего
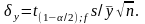 (2.4)
(2.4)
На
основании полученного уравнения можно
решить задачи определения объема
выборки. Располагая данными о вариационном
коэффициенте
 ,
полученном из предварительных испытаний,
в зависимости от требуемой относительной
ошибки у
вычисляем значение коэффициента k:
,
полученном из предварительных испытаний,
в зависимости от требуемой относительной
ошибки у
вычисляем значение коэффициента k:
 (2.5)
(2.5)
с помощью которого по табл. П 2 приложения находим необходимый объем выборки.
Дисперсия может использоваться как характеристика точности применяемой методики исследований, для оценки стабильности технологических процессов и т.д.
Распределение
величины
 (
( квадрат-распределение) зависит только
от числа степеней свободы
квадрат-распределение) зависит только
от числа степеней свободы
 .
В отличие от
.
В отличие от
 -распределения
распределение
-распределения
распределение
 несимметрично. Квантили распределения
приведены в табл. П3 приложения.
несимметрично. Квантили распределения
приведены в табл. П3 приложения.
С
доверительной вероятностью р=1- справедливо неравенство, являющееся
доверительной оценкой генеральной
дисперсии:
справедливо неравенство, являющееся
доверительной оценкой генеральной
дисперсии:
 (2.6)
(2.6)
Для генерального среднего квадратического отклонения такая оценка имеет вид
 (2.7)
(2.7)
В
ряде исследованиях наибольший интерес
представляют верхние границы дисперсии
и генерального среднего квадратического
отклонения как характеризующие наибольшую
изменчивость исследуемого признака.
Представив их как
 и
и
 ,
получим следующие выражения:
,
получим следующие выражения:
 (2.8)
(2.8)
 (2.9)
(2.9)
на
основании которых в зависимости от
относительной ошибки определения
дисперсии
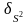 или среднего квадратического отклонения
или среднего квадратического отклонения
 и принятой доверительной вероятности
(1-
)
возможно (с помощью табл. П4) определение
минимального объема выборки.
и принятой доверительной вероятности
(1-
)
возможно (с помощью табл. П4) определение
минимального объема выборки.
Фактический объем выборки следует брать с некоторым запасом. После проведения исследований определяем фактическую погрешность определения искомых параметров.
При проведении исследований часто возникает вопрос, можно ли считать сравниваемые выборочные дисперсии оценками одной и той же генеральной дисперсии (например, считать сравниваемые технологические процессы одинаково стабильными).
Рассмотрим
метод сравнения двух дисперсий
 и
и
 ,
имеющих соответственно
,
имеющих соответственно
 и
и
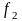 степеней
свободы. Предположим, что первая выборка
сделана из генеральной совокупности с
дисперсией
степеней
свободы. Предположим, что первая выборка
сделана из генеральной совокупности с
дисперсией
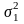 ,
вторая – с дисперсией
,
вторая – с дисперсией
 .
Выдвигается так называемая нулевая
гипотеза о равенстве
.
Выдвигается так называемая нулевая
гипотеза о равенстве
 .
Чтобы отвергнуть эту гипотезу, нужно
показать значимость расхождения между
и
при принятом уровне значимости
.
В качестве критерия значимости
используются квантили распределения
Фишера или
.
Чтобы отвергнуть эту гипотезу, нужно
показать значимость расхождения между
и
при принятом уровне значимости
.
В качестве критерия значимости
используются квантили распределения
Фишера или
 -
распределения
(табл. П 5):
-
распределения
(табл. П 5):
 (2.10)
(2.10)
Если обозначить через большую из сравниваемых дисперсий, то нулевую гипотезу (гипотезу о равенстве дисперсий) следует отбросить при
 (2.11)
(2.11)
Когда
отношение дисперсий меньше критического
значения
,
сравниваемые
выборочные дисперсии являются однородными,
т. е. оценками одной и той же генеральной
совокупности. В таких случаях для
генеральной дисперсии может быть
получена средневзвешенная оценка
 c
c
 степенями
свободы:
степенями
свободы:
 (2.12)
(2.12)
Рассмотрим
метод сравнения нескольких дисперсий

 имеющих
равные числа степеней свободы
имеющих
равные числа степеней свободы
 .
В этом случае, если отношение наибольшей
дисперсии ко всей сумме дисперсий больше
квантиля распределения Кохрана (табл.
П6) с определенным уровнем значимости
,
то расхождение между дисперсиями нужно
считать значимым,
т. е. при
.
В этом случае, если отношение наибольшей
дисперсии ко всей сумме дисперсий больше
квантиля распределения Кохрана (табл.
П6) с определенным уровнем значимости
,
то расхождение между дисперсиями нужно
считать значимым,
т. е. при
 (2.13)
(2.13)
нулевая гипотеза (о равенстве дисперсий) отвергается.
Рассмотрим
метод сравнения двух средних
 и
и
 .
Вначале нужно проверить равенство
дисперсий
и
с
помощью
-критерия
Фишера. Если нулевая гипотеза о равенстве
.
Вначале нужно проверить равенство
дисперсий
и
с
помощью
-критерия
Фишера. Если нулевая гипотеза о равенстве
 не отвергается, то вычисляется
средне-взвешенная дисперсия
(2.12) с
степенями свободы. Затем расматривается
нулевая гипотеза
не отвергается, то вычисляется
средне-взвешенная дисперсия
(2.12) с
степенями свободы. Затем расматривается
нулевая гипотеза
 .
Критерием проверки этой гипотезы
являются квантили
–
распределения. Гипотеза о равенстве
средних отвергается, при
.
Критерием проверки этой гипотезы
являются квантили
–
распределения. Гипотеза о равенстве
средних отвергается, при
 (2.14)
(2.14)
В
оценке используются квантили величины
,
соответствующие
 степеням
свободы.
степеням
свободы.
Если
дисперсии
и
оказываются неоднородными, пользуются
приближенным критерием
 для проверки гипотезы о равенстве
генеральных средних:
для проверки гипотезы о равенстве
генеральных средних:
 (2.15)
(2.15)
Нулевая
гипотеза
отклоняется,
если окажется что
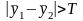 .
.
Для
оценки существенности различий
коэффициентов вариации используется
 -критерий,
подсчитываемый по уравнению
-критерий,
подсчитываемый по уравнению
 (2.16)
(2.16)
При >3 различие коэффициентов вариации полагают значимым.
Одно из важных условий правильного применения статистических методов заключается в отсутствии грубых ошибок в исследованиях. При этом единственный надежный способ – тщательный анализ условий самих испытаний. Результаты, полученные в нарушенных условиях, должны отбрасываться независимо от того, насколько они отличаются от предыдущих измерений. Когда такой анализ провести не удается, сомнению, как правило, подвергаются самый большой и самый малый (крайний) элементы выборки.
Если
( - крайний элемент выборки, по которой
подсчитаны
- крайний элемент выборки, по которой
подсчитаны
 и
и
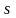 и
и
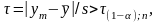 (2.17)
(2.17)
то
величина
отбрасывается как грубо ошибочная
величина (на уровне значимости
),
после чего заново нужно вычислить
значения
 и
.
Значение квантилей
и
.
Значение квантилей
 -распределения
приведены в табл. П7. В случаях, когда
сомнение вызывают несколько элементов
выборки, поступают следующим образом.
Для каждого из них вычисляется величина
и исследование назначают с элемента,
имеющего наименьшее значение
.
Остальные сомнительные элементы из
рассмотрения временно исключаются, и
для такой уменьшенной выборки (в которой
остался лишь один сомнительный элемент)
вычисляются значения
-распределения
приведены в табл. П7. В случаях, когда
сомнение вызывают несколько элементов
выборки, поступают следующим образом.
Для каждого из них вычисляется величина
и исследование назначают с элемента,
имеющего наименьшее значение
.
Остальные сомнительные элементы из
рассмотрения временно исключаются, и
для такой уменьшенной выборки (в которой
остался лишь один сомнительный элемент)
вычисляются значения
 и
.
Если это
не
превышает табличное
и
.
Если это
не
превышает табличное
 ,
(число
степеней свободы соответствует
первоначальному объему выборки до всех
отбрасываний), то сомнительный элемент
присоединяется к выборке и начинают
исследовать следующий сомнительный
элемент, вычисляя заново
и
.
Если же
превосходит табличное значение, то
сомнительное значение является ошибочным,
тем более ошибочными будут и ранее
отброшенные сомнительные значения.
,
(число
степеней свободы соответствует
первоначальному объему выборки до всех
отбрасываний), то сомнительный элемент
присоединяется к выборке и начинают
исследовать следующий сомнительный
элемент, вычисляя заново
и
.
Если же
превосходит табличное значение, то
сомнительное значение является ошибочным,
тем более ошибочными будут и ранее
отброшенные сомнительные значения.
