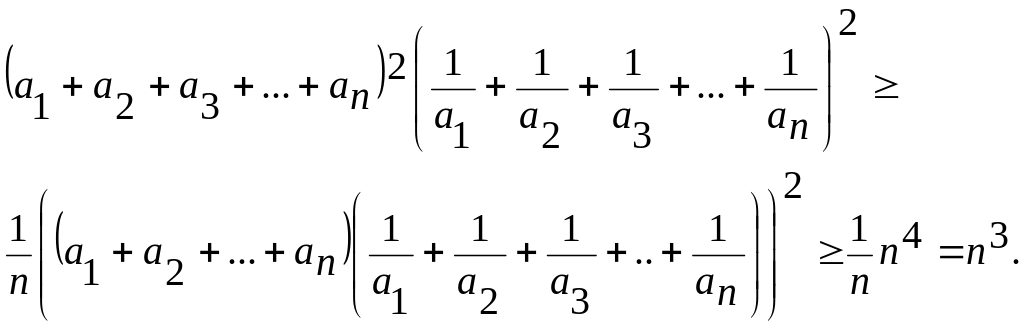1.4 Теорема про нерівність для наборів з n чисел

Розглядаємо два набори чисел, які складаються з n чисел , . Запишемо число, яке позначимо: Нехай - перестановка чисел (таких перестановок n! ).

Теорема 3. Нехай і - одномонотонні послідовності , а послідовність - це перестановка чисел , тоді має місце така нерівність . Якщо послідовності протилежно монотонні, то знак нерівності змінюється на протилежний.

Доведення. Нам треба довести, що із усіх чисел максимальним серед них буде число . Послідовність відрізняється від , тому знайдеться пара чисел така, що послідовності і не одномонотонні, отже, помінявши місцями числа і , ми збільшимо суму , а значить і усю суму .

Приклад 7. Довести , що для додатних дійсних чисел a, b, c , d має місце нерівність .

Розв’язання. Нехай , тоді запишемо перерозміщувальну нерівність , що треба було довести.

Приклад 8. Нехай - додатні дійсні числа, . Довести , що для додатних дійсних чисел .

Розв’язання. Послідовності і 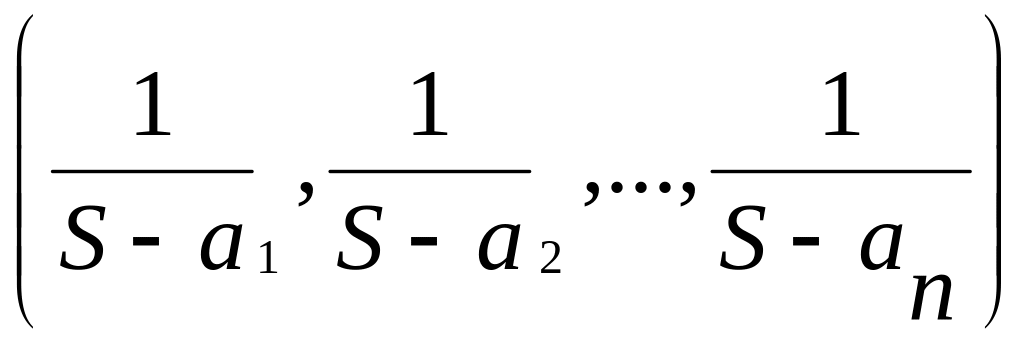- одномонотонні. Запишемо ліву частину даної нерівності . Запишемо перерозміщувальну нерівність . Додавши почленно ці нерівності, отримаємо нерівність, яку треба було довести.

Приклад 9. Нехай - додатні дійсні числа. Довести, нерівність .

Розв’язання. Послідовності і 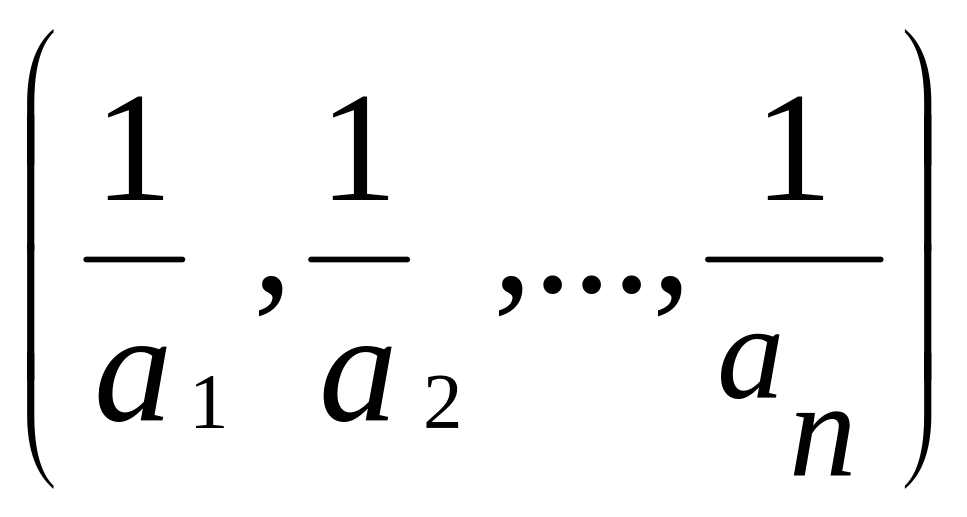- протилежно монотонні. Запишемо перерозміщувальну нерівність для цих послідовностей :

. Нерівність доведено.

Зауважу, що при розв’язанні цієї задачі можна було починати з одномонотонних послідовностей: . Помноживши обидві частини нерівності на -1, отримаємо потрібну нерівність.

Приклад 10. Нехай - додатні дійсні числа. Довести, нерівність .

Розв’язання. Послідовності і одномонотонні. Для лівої частини даної нерівності запишемо перерозміщувальну нерівність і отримали потрібну нерівність.

Розділ 2 Доведення нерівностей за допомогою перерозміщувальних нерівностей

1. Нерівність Чебишова і її наслідки

Розглянемо дві одномонотонні послідовності і . Для цих послідовностей запишемо n перерозміщувальних нерівностей :

1. ;

2. ;

3. ;

...............................................................................

n.

Додамо почленно усі n нерівностей і отримаємо нову нерівність . Ця нерівність називається нерівністю П.Л. Чебишова, який її довів і використав у своїх наукових працях.

Якщо розглядати протилежно монотонні послідовності, то у нерівності Чебишова треба змінити знак нерівності на протилежний. Отже, якщо і - протилежно монотонні послідовності, то має місце нерівність .

Приклад 11. Довести нерівність , де а,b,c – додатні дійсні числа.

Розв’язання. Розглянемо дві числові послідовності і . Це одномонотонні послідовності, тому запишемо для них нерівність Чебишова . Виконавши тотожні перетворення останньої нерівності, отримаємо нерівність , , яку треба було довести.

Приклад 12. Нехай - довільні дійсні числа. Довести, що .

Розв’язання. Запишемо нерівність Чебишова для двох одномонотонних послідовностей і і отримаємо нерівність , що треба було довести.

Приклад 13. Нехай - додатні дійсні числа. Довести, що .

Розв’язання. Розглянемо одномонотонні послідовності і . Запишемо для цих послідовностей нерівність Чебишова:

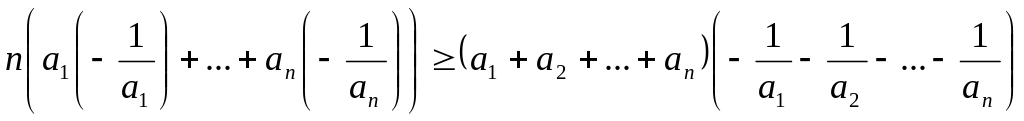, або , звідки, помноживши обидві частини на -1, отримаємо вірну нерівність: .

Приклад 14. Нехай - додатні дійсні числа. Довести, що .

Розв’язання.

1. Виконаємо тотожні перетворення даної нерівності:

.

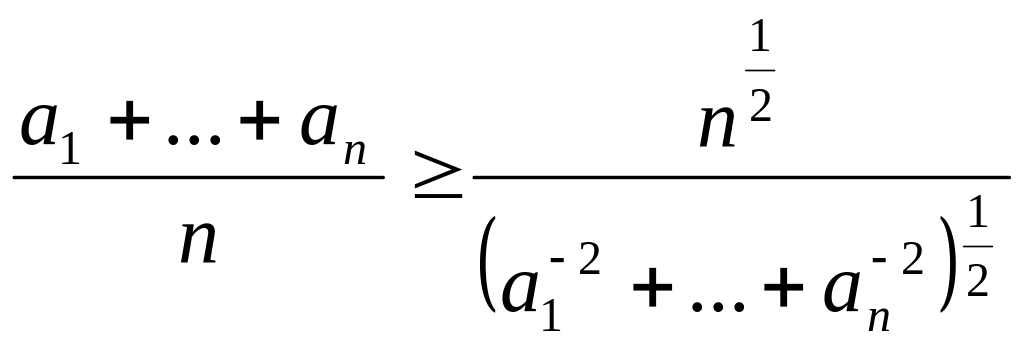
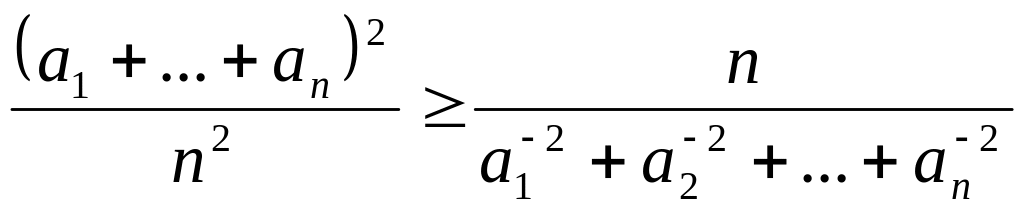
2. За нерівністю Чебишова маємо .

3. За нерівністю Чебишова запишемо таку нерівність