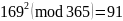2.4. Возведение в степень и нахождение порождающего элемента группы

Приведенный шаблон реализует так называемое «наивное» модульное возведение в степень в конечном поле. Для примера взято поле F₁₉. Заносим его элементы в первую строку таблицы, а в ячейку A2 вводим формулу (рис. 7).

Рис. 7. Исходная формула

Распространяем формулу на диапазон ячеек A2:R18

Рис. 8. Таблица Кэли с выделенными примитивными элементами

В результате получилась таблица Кэли для возведения в степень по модулю 19. Особое внимание обратим на столбцы, выделенные серым цветом. В них многократное применение операции умножения к заглавным элементам столбцов образует полную перестановку элементов поля. Такие элементы называют порождающими или примитивными. Кроме того, следует обратить внимание на последнюю строку таблицы (все единицы). Она хорошо иллюстрирует малую теорему Ферма:

На практике наивное возведение в степень оказывается неэффективным. Приведем алгоритм бинарного модульного возведения в степень. В основе алгоритма лежит схема Горнера. Проиллюстрируем ее на конкретном примере [8]:

что в итоге вместо 26 умножений дает 4 возведения в квадрат и 3 умножения. Для больших чисел экономия становится еще более значительной. Заметим, что последовательность возведений в квадрат и удвоений соотносится с двоичным представлением показателя степени:

Начиная со второго старшего двоичного разряда, при 1 возвести в квадрат и домножить, при 0 возвести в квадрат.

Алгоритм бинарного модульного экспоненцирования [1].

Представить показатель степени в двоичном виде:

Присвоить

Для i от 1 до r: ;

Задача 2.3. Возвести число x в степень y по модулю числа N, используя метод бинарного модульного экспоненцирования.

Пример решения.

Дано: x = 134 y = 344 N = 365	Решение:

		y_i
Найти:		0
x^y mod N		1
		0
		1
		1
		0
		0
		0

2.5. Генерация простых чисел

Детерминированной зависимости распределения простых чисел не существует. Также не существует детерминированного алгоритма их генерации. Наилучшие результаты дают вероятностные тесты числа на простоту, из которых на практике наиболее применим тест Рабина-Миллера [13]:

Выбрать для тестирования число p. Вычислить b – число делений p – 1 на 2 (то есть 2^b – это наибольшая степень числа 2, на которую делится p – 1). Затем вычислить m, такое, что p = 1 + 2^b · m.

Далее для генерации простого p:

Выбрать случайное число a, меньшее p.
Установить j = 0 и z = a^m mod p.
Если z = 1 или если z = p – 1, то p проходит тест и может быть простым числом.
Если j > 0 и z = 1, то p не относится к простым числам.
Установить j = j + 1. Если j < b и z  (p – 1), установить
z = z² mod p и вернуться к шагу 4. Если z = p – 1, то p проходит тестирование и может быть простым числом.
Если j = b и z  (p – 1), то p не относится к простым числам.