3.4. Криптосистема Эль-Гамаля
В данной системе исправлен недостаток RSA по однозначному шифрованию. В самой схеме заложено присутствие случайного элемента – эфемерного сеансового ключа k, передаваемого в сообщении неявным образом. Кроме того, система позволяет использовать общие для всех абонентов параметры, аналогичные протоколу Диффи-Хеллмана – простое число P и примитивный элемент G.
Каждый абонент системы генерирует секретный ключ
.
Открытый
ключ Y
вычисляют как:
Абонент,
желающий зашифровать сообщение m
выбирает сеансовый ключ
.
Обязательность соблюдения условий
и аналогична протоколу Диффи-Хеллмана.
Особенностью
(и недостатком) шифрования является то,
что сообщение при шифровании удваивается
по длине и представляет собой пару
-
первая часть сообщения, не зависящая
от открытого текста. C1
служит для неявной передачи эфемерного
ключа и из-за независимости от шифруемого
сообщения может быть выработано заранее
в фоновом режиме.
-
вторая часть сообщения, служащая
собственно для передачи m.
Расшифрование сообщения производится как:
.
Приведем краткое доказательство работоспособности, в котором для удобства опущены операции приведения по модулю:
Недостатком системы также является необходимость помимо возведения в степень при расшифровании применить обобщенный алгоритм Евклида, что отрицательно сказывается на скорости вычислений.
Задача 3.4. Для заданного простого числа P и открытого текста m определить самостоятельно минимальный порождающий элемент G и остальные параметры шифрсистемы Эль-Гамаля, осуществить зашифрование и расшифрование. Проверить совпадение исходного m и полученного значений открытого текста.
Пример решения
Дано: P = 131 m = 59 |
Решение:
|
Найти: Gmin, x, Y, k, C1, C2, m’ Проверить: m’ = m |
|
|
|
3.5. Криптосистема Рабина
Данная система не получила широкого применения, но приведена здесь для иллюстрации возможности использовать при асимметричном шифровании операции модульного возведения в квадрат. Система основана на трудности извлечения квадратного корня по модулю составного числа без знания разложения модуля на множители.
Каждый
абонент выбирает собственную пару
простых чисел p
и q,
с соблюдением следующего требования:
,
что позволит извлекать квадратный
корень, не прибегая к алгоритму Шенкса.
Затем
вычисляют
и выбирают
Открытым
ключом является пара
Закрытым
ключом является пара
Особенностью системы является очень простая и быстрая операция зашифрования :
Для расшифрования необходимо вычислить:
Приведем краткое доказательство работоспособности, в котором для удобства опущены операции приведения по модулю:
Для
удобства вычислений принимаем
и
соответственно
Извлечение корней производится по модулю простых чисел p и q:
.
Каждое из сравнений дает по два корня, соответственно вариантов значения si получается всего четыре (что является основным недостатком системы). Найдем их попарно, при помощи КТО и свойства корней:
Четыре варианта расшифрования получим, выполнив вычисления:
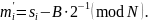
Для распознавания правильного варианта расшифрования, как правило, вводят некоторую обратимую функцию избыточности F(m), позволяющую с высокой вероятностью выбрать правильный вариант, например F(m) = 44||m.
Задача 3.5. Для заданной пары простых чисел p и q и открытого текста m определить самостоятельно остальные параметры шифрсистемы Рабина и осуществить зашифрование и расшифрование. Проверить совпадение исходного m и одного из четырех полученных mj’ значений открытого текста.
Пример решения
Дано: p = 127 q = 131 m = 4410 = 44||10 |
Решение:
|
|
Найти: N, B, C, m1-4’ Проверить:
|
||
|
||
|
|
|
|
||
mi’
= m
