Тригонометрическая форма числа

Из геометрических соображений видно, что . Тогда комплексное число можно представить в виде:

Такая форма записи называется тригонометрической формой записи комплексного числа.

При этом величина r называется модулем комплексного числа, а угол наклона  - аргументом комплексного числа.

.

Из геометрических соображений видно:

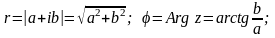
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.

Действия с комплексными числами

Основные действия с комплексными числами вытекают из действий с многочленами.

1) Сложение и вычитание

2) Умножение

В тригонометрической форме:

,

С случае комплексно – сопряженных чисел:

3) Деление

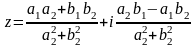
В тригонометрической форме:

4) Возведение в степень

Из операции умножения комплексных чисел следует, что

В общем случае получим:

,

где n – целое положительное число.

Это выражение называется формулой Муавра.

(Абрахам де Муавр (1667 – 1754) – английский математик)

Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.

Пример. Найти формулы sin2 и cos2.

Рассмотрим некоторое комплексное число

Тогда с одной стороны .

По формуле Муавра:

Приравнивая, получим

Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то

Получили известные формулы двойного угла.

5) Извлечение корня из комплексного числа

Возводя в степень, получим:

Отсюда:

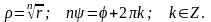
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.

Пример. Даны два комплексных числа . Требуется а) найти значение выражения в алгебраической форме, б) для числа найти тригонометрическую форму, найти z²⁰, найти корни уравнения

1. Очевидно, справедливо следующее преобразование:

Далее производим деление двух комплексных чисел:

Получаем значение заданного выражения: 16(-i)⁴ = 16i⁴ =16.

б) Число представим в виде , где

Тогда .

Для нахождения 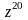воспользуемся формулой Муавра.

Если , то

Дифференциальное исчисление функции одной переменной

Производная функции, ее геометрический и физический смысл

Определение. Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

у

f(x)

f(x₀ +x) P

f

f(x₀) M

  x

0 x₀ x₀ + x x

Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МР к графику функции.

,

где  - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой:

Уравнение нормали к кривой: .

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.