Уравнение Бернулли.
Определение. Уравнением Бернулли называется уравнение вида
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для
решения уравнения Бернулли применяют
подстановку
,
с помощью которой уравнение Бернулли
приводится к линейному.
Для этого разделим исходное уравнение на yn.
Применим
подстановку, учтя, что
.
Т.е. получилось линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:
Пример.
Решить уравнение
Разделим
уравнение на xy2:
Полагаем
.
Полагаем
Произведя обратную подстановку, получаем:
Пример.
Решить уравнение
Разделим
обе части уравнения на
Полагаем
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
Получаем:
Применяя обратную подстановку, получаем окончательный ответ:
Уравнения вида y = f(y’) и x = f(y’).
Решение уравнений, не содержащих в одном случае аргумента х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную неизвестной функции.
Для
уравнения первого типа получаем:
Делая
замену, получаем:
В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.
Общий интеграл в параметрической форме представляется системой уравнений:
Исключив из этой системы параметр р, получим общий интеграл и не в параметрической форме.
Для дифференциального уравнения вида x = f(y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат:
Дифференциальные уравнения высших порядков.
Определение. Дифференциальным уравнением порядка n называется уравнение вида:
В некоторых случаях это уравнение можно разрешить относительно y(n):
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.
Определение.
Решение
удовлетворяет начальным условиям
,
если
Определение. Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши.
Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.
Рассмотрим подробнее методы нахождения решений этих уравнений.
Уравнения, допускающие понижение порядка.
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y(n) = f(x).
Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.
…………………………………………………………….
Пример.
Решить уравнение
с начальными условиями x0=0;
y0=1;
Подставим начальные условия:
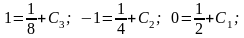
Получаем
частное решение (решение задачи Коши):
.