Ряд Фурье для четных и нечетных функций

Отметим следующие свойства четных и нечетных функций:

1)

2) Произведение двух четных и нечетных функций является четной функцией.

3) Произведение четной и нечетной функций – нечетная функция.

Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций.

Если f(x) – четная периодическая функция с периодом 2, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:

Таким образом, для четной функции ряд Фурье записывается:

Аналогично получаем разложение в ряд Фурье для нечетной функции:

Пример. Разложить в ряд Фурье периодическую функцию с периодом T = 2 на отрезке [-;].

Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

Получаем:

.

Ряды Фурье для функций любого периода

Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [-l, l] имеет вид:

Для четной функции произвольного периода разложение в ряд Фурье имеет вид:

Для нечетной функции:

Контрольная работа №2 «Дифференциальные уравнения»

Вариант 1

Задание 1

Найти общее решение дифференциального уравнения:

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Материальная точка массой m = 2 г. погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности k = 0,002 кг/с. Найти скорость точки через 1 с. после начала погружения, если в начальный момент она была равна нулю.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 2

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Моторная лодка двигалась в спокойной воде со скоростью км/ч. На полном ходу ее мотор был выключен, и через 10с скорость лодки уменьшилась до 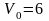км/ч. Сила сопротивления воды пропорциональна скорости движения лодки. Найти скорость лодки через 1мин после остановки мотора.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .