5.4.4 Определение выражений для тока и напряжений

Выражения для остальных токов и напряжений определяется из системы уравнений, составленной по законам Кирхгофа (5.40).

. (5.50)

Выражения для тока i₂ получается из второго уравнения системы (5.40) после подстановки выражений (5.50) и (5.37).

. (5.51)

Выражения для напряжения u_c конденсатора получается из третьего уравнения системы (4.36).

. (5.52 )

Ток конденсатора i_c определяется из выражения i_c = после подстановки в него уравнения (5.52).

. (5.53)

6 Методические указания по расчету переходных процессов в цепях при действии источника, изменяющегося

по синусоидальному закону

Уравнение, определяющее любую переменную цепи: токи в ветвях, напряжение на элементах, в общем случае содержит две составляющие: вынужденную и свободную. Свободная составляющая определяется решением однородного дифференциального уравнения, то есть, уравнением без правой части. Значит вид свободной составляющей не зависит от вида источника, действующего в цепи, а определяется только схемой соединения элементов цепи и их параметрами.

Вынужденная составляющая искомой переменной зависит от вида источника, действующего в цепи. Расчет вынужденной составляющей при действии источника синусоидальной формы производится в комплексной форме.

Кроме расчета вынужденной составляющей необходимо обратить внимание на определение начальных условий при определении постоянных интегрирования. В этом случае производится расчет значений токов и напряжений в комплексной форме для цепи до коммутации. Затем найденные значения переменных записываются в синусоидальной форме и в полученные выражения подставляется t=0. Рассмотрим расчет начальных значений переменных на примере цепи, приведенной на рис.6.1.

Рисунок 6.1

На входе цепи действует напряние, изменяющееся по синусоидальному закону Определим токи в ветвях схемы комплексным методом.

Запишем напряжение источника в комплексной форме:

.

Определим входной ток цепи до коммутации

, где . (6.1)

Тогда выражение для тока в комплексной форме будет иметь вид:

.

Выразим токи и через параметры цепи:

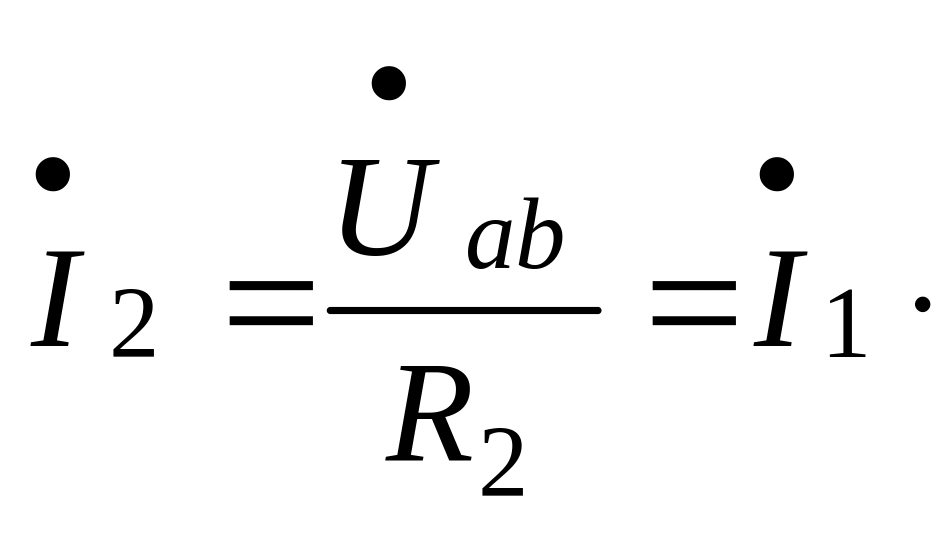
, (6.2)

. (6.3)

Тогда выражение для токов и будут иметь следующий вид:

= , = . (6.4)

Запишем токи цепи в синусоидальной форме:

(6.5)

Подставим в полученные выражения t=0 и найдем значения этих токов в момент времени непосредственно перед коммутацией.

(6.6)

Аналогично находятся начальные значения напряжений на элементах цепи.

7 Методические указания по расчету переходных процессов

операторным методом

7.1 Общая методика расчета переходных процессов

операторным методом

7.1.1 Основные положения и соотношения

В основу операторного метода положено следующее: функция f(t), которая является током i(t) или напряжением u(t), называется оригиналом, заменяется соответствующей ей функцией F(p) комплексного переменного p, называемой изображением. Эти функции связаны соотношением, называемым прямым преобразованием Лапласа

, (7.1)

или . (7.2)

При таком преобразовании операция дифференцирования над функцией вещественного переменного f(t) заменяется операцией умножения на оператор p функции комплексного переменного F(p). В свою очередь операция интегрирования заменяется операцией деления на оператор p.

В таблице 7.1 приводятся оригиналы простейших функций и их изображения, полученные по формуле (7.1) .

Таблица 7.1

№	Оригинал	Изображение	№	Оригинал	Изображение
1	1		8
2	t		9

Продолжение таблицы 7.1

№	Оригинал	Изображение	№	Оригинал	Изображение
3			10
4			11
5			12
6			13
7			14

Схемы замещения реактивных элементов, составленные по формуле 7.1 цепи с ненулевыми начальными условиями, приведены на рис. 7.1.

Индуктивный элемент	Емкостной элемент
.	.
Рисунок 7.1 Схемы замещения реактивных элементов