1. Ур. Максвелла в интегральной и дифференциальной формах.

Под электромагнитным полем (ЭМП) следует понимать среду, пространственно-временное состояние которой полностью определяется четырьмя векторами:

(х,y,z,t) – вектор напряженности электрического поля.

(x,y,z,t) – вектор электрического смещения.

(x,y,z,t) – вектор индукции магнитного поля.

(x,y,z,t) – вектор напряженности магнитного поля.

Будем рассматривать ЭМП в объеме V с граничной поверхностью S, на которой происходит скачок свойств среды. Во всех внутренних точках V, т.е. точках, не принадлежащих S, векторы поля непрерывны вместе с первой и второй производными по координатам, а также конечны. Эти векторы удовлетворяют четырем уравнениям Максвелла (УМ):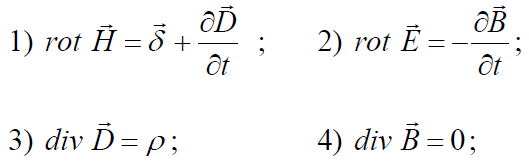

Первое УМ – обобщение закона Ампера, в соответствии с которым:

В первом УМ член 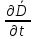- плотность тока смещения.

Для перехода к интегральной форме записи первого УМ воспользуемся теоремой Стокса для некоторой поверхности S, опирающейся на контур l . Проинтегрируем обе части уравнения по S:

Применяя к левой части теорему Стокса, получим:

Где – электрический ток через поверхностьS, - ток смещения через эту поверхность.

Второе УМ – обобщение закона электромагнитной индукции.

Интегральная форма этого уравнения получается из дифференциальной тем же путем, что и первое уравнение. В результате применения теоремы Стокса в левой части получаем:

Третье уравнение Максвелла является обобщением уравнения Гаусса-Кулона на случай произвольной среды. Применяя интегрирование по V с границей S к обеим частям уравнения и используя теорему Остроградского-Гаусса к левой части, получим:

Четвертое уравнение Максвелла утверждает отсутствие магнитных за рядов и одновременно постулирует его справедливость для любой среды. Те же действия, как и в предыдущем случае, дают интегральную форму этого уравнения:

2. Закон сохранения заряда и его связь с током смещения в 1-м ум.

Центральным постулатом теории Максвелла является закон сохранения заряда. Полагается, что сумма электрических в мировом пространстве постоянна. Заряды не возникают и не исчезают. Причиной изменения величины заряда в данном объеме V является перемещение зарядов, т.е. электрический ток через ограничивающую этот объем поверхность S. Иначе говоря, можно утверждать для V с границей S:

Представим q и как:

Тогда:

Применим к левой части теорему Остроградского-Гаусса и положим, что V не зависит от t, при этом получим:

Поскольку объем произволен, последнее равенство может выполнятся только при условии:

Данное условие называется уравнением непрерывности.

3. Материальные уравнения и классификация сред.

В общем случае зависимости имеют линейный характер.

Рассмотрим векторную функцию и разложим её в ряд Маклорена:

Здесь

Рассмотрим линейный случай, когда квадратичным и высшими членами разложения можно пренебречь:

Или в подробной записи:

Обозначим:

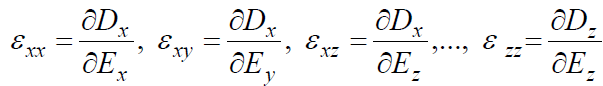
Введем тензор:

Используя тензор диэлектрической проницаемости, уравнение для линейных сред можно записать в следующей форме:

Аналогичным образом вводятся тензоры магнитной проницаемости и удельной проводимости:

Среда называется изотропной, если , при условии:

Тогда материальные уравнения имеют вид:

Среда называется однородной, если не зависят от координат в рассматриваемом объеме.

В противном случае среда называется неоднородной.