Шпоры и задачи 2012 (Саломатин) [7171 вопросов] / scr / doc / 31-36

31. Характеры ДПФ

Дискретное преобразование Фурье устанавливает связь между временным и частотным представлениями сигнала при разложении его по гармоническим дискретно экспоненциальным функциям. Дискретные прямое и обратное преобразования Фурье по базисам из идеальных отсчетных функций:

имеют следующий вид: (Х(к)- прямое ДПФ; х[n]-обратное ДПФ )

где {x[n]}- последовательность отсчетов сигнала

{X(k)} – последовательность спектральных коэффициентов:

- интервалы дискретизации сигнала x(t) и его спектра Фурье X(f);

Здесь характеры есть базисные функции преобразования, равные степеням КОРНЕЙ из 1

32. Базисы характеров дискретных преобразований

Базисные функции:

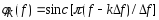
ДПФ:

ОДПФ:

,

{x[n]}- последовательность отсчетов сигнала:

{X(k)} – последовательность спектральных коэффициентов:

;

и - интервалы дискретизации сигнала x(t) и его спектра Фурье X(f); .

33. Спектральный анализ сигналов с помощью текущего, взвешенного ДПФ.

Спектральный анализ – это один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала.

Спектральная плотность мощности стационарных процессов, статистические характеристики которых не меняются (плотность распределения вероятности и в первом приближении математическое ожидание, дисперсия), удобно вычислять коррелограммным алгоритмом. В случае нестационарных процессов СПМ будет изменяться во времени. Для отображения изменения спектра во времени вводится временная ось, и СПМ уже является функцией частоты и времени. Такой подход вычисления СПМ используется в частотно-временных преобразованиях. Под частотно-временным преобразованием понимается некоторая совместная функция времени и частоты, характеризующая распределение спектра в частотно- временной плоскости. Простым примером является текущее преобразование Фурье:

где x[n]– дискретные отсчеты сигнала; n, k – индексы дискретных отсчетов по времени и частоте соответственно; L – длина дискретного преобразования Фурье. Результат F[k,n] вычисляется в координатах частота – время.

Весовая функция окна (оконная функция или просто «окно») используется для

управления эффектами, обусловленными наличием боковых лепестков в

спектральных оценках. Наличие боковых остатков (боковых лепестков) приводит к

амплитудным ошибкам в спектре и к маскированию присутствующих слабых

сигналов. Основное назначение функции окна – уменьшить величину смещения и

уровень боковых остатков (боковых лепестков) в СПМ.

Дискретное преобразование Фурье от взвешенной окном последовательности есть свертка спектров сигнала x[n] и окна w[n]:

где X ( f ) – преобразование от сигнала x[n];

- ядро Дирихле или дискретная функция «sinc», которая является преобразованием от прямоугольной функции (в данном случае w[n] – прямоугольное окно).

Из выражения видно, что спектр является искаженным относительно X ( f ) функцией окна.

Известен ряд весовых функций, которые в большей или в меньшей степени снижают боковые остатки. Снижение уровня боковых остатков достигается ценой

расширения главного лепестка спектра окна, что приводит к ухудшению разрешения.

Следовательно, должен выбираться какой-то компромис между шириной главного

лепестка и уровнем подавления боковых лепестков.

Текущее преобразование Фурье можно дополнить, умножив сигнал на весовое

окно w[l] (получим взвешенное ДПФ):

34. КИХ-фильтр: оптимальный частотный фильтр.

Особенность – линейная ФЧХ, устойчивость

Проектирование:

1.теоретический синтез - методы оптимизации (критерии: min взвешенной СКО, минимаксный критерий)

2.на практике методы:

идеальная ИХ+выбор оконной функции,

ЧХ с равными боковыми лепестками.

КИХ фильтр = конечная ИХ фильтра.

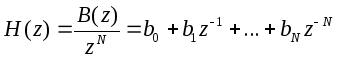
Фильтры «скользящего типа».Полюс при z=0 (стабильная структура). N нулей (нули B(z)), дает фильтры «все нули»

Разностное уравнение:

Импульсная характеристика:

Схема КИХ:

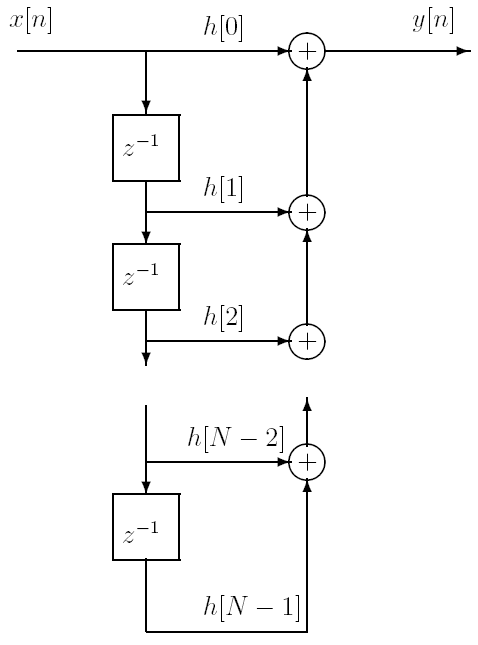
КИХ-фильтры с ЛФЧХ.Тип-1

N=2L=четное; Симметричная импульсная характеристика; h[k]=h[N-k];

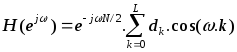
Типы фильтров: НЧ/ВЧ/ПФ

КИХ-фильтры с ЛФЧХ. Тип-2

N=2L+1=нечетное;Симметричная импульсная характеристика;h[k]=h[N-k] ;

нуль в

Типы фильтров: НЧ/ПФ

КИХ-фильтры с ЛФЧХ. Тип-3

N = 2L = четное;антисимметричная импульсная характеристика h[k] = – h[N – k]

нуль в

Типы фильтров: ПФ

КИХ-фильтры с ЛФЧХ.Тип-4

N = 2L+1 = нечетное; антисимметричная импульсная характеристика

h[k] = – h[N – k]

нуль в

Типы фильтров: ВЧ

Фильтры 1 типа – универсальны. Фильтры 3 и 4 типов – часто используются при проектировании дифференциаторов и фильтров, реализующих преобразование Гильберта, поскольку они могут давать сдвиг фазы на 90º

Разработка КИХ-фильтров:

1.Спецификация фильтра

2.Вычисление коэффициентов

3. Выбор структуры

4. Анализ следствий конечной разрядности

5.Воплощение

35. Проектирование КИХ-фильтра по методу частотной дискретизации

Выберем базисную форму для получения ЛФЧХ. Например, для Тип-1:

Спецификация желаемой ЧХ (НЧ, ВЧ, ПФ,…) :

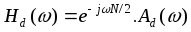
Критерий оптимизации:

Где - весовая функция

Синтез через оптимизацию:

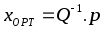
Решение оптимизации квадратичной формы:

Функция оптимизации:

Окно:

Критерий минимакса Minimax:

Где весовая функция

Исходные данные задаются по желаемой АЧХ и ФЧХ

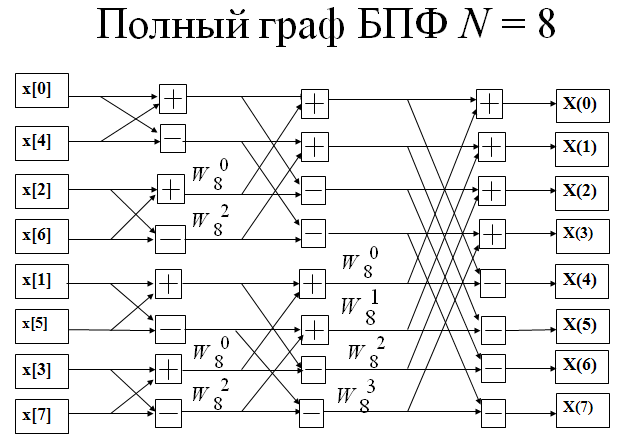
36. Быстрое преобразование Фурье с прореживанием во времени

Исходная последовательность

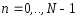
разбивается на две последовательности длиной N/2, соответствующие четным и нечетным отсчетам

Вычисление N-точечного ДПФ в этом случае сводится к двум N/2- точечным ДПФ N/2 умножениям на поворачивающие фазовые множители и N сложениям:

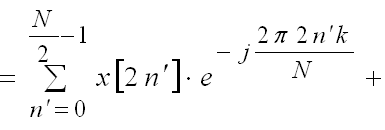
ДПФ -> 2 ДПФ (N/2):

Структура «бабочка»: Для k = 0,…, N –1 получаем

На втором шаге данная процедура применяется для замены двух N/2-точечных ДПФ на четыре N/4- точечные ДПФ. Далее, каждое ДПФ N/4 расщепляется на два ДПФ N/8 .

Эта процедура продолжается до тех пор, пока не останутся только двухточечные ДПФ.

Вычислительная сложность N-точечных ДПФ, N=2^m

Требуется m = log N шагов, на каждом из которых:

– точечных ДПФ сводятся к – точечным ДПФ;

каждая итерация выполняет N сложений и N/2 умножений на поворачивающие множители

Вычислительная сложность: Сложность N-точечного ДПФ методом прореживания по времени составляет (N/2)log₂N операций комплексного умножения и N log₂ N операций комплексного сложения.