Шпоры и задачи 2012 (Саломатин) [7171 вопросов] / scr / doc / 67

67.ТЧП ФЕРМА

Число Ферма имеет вид , где t — положительное целое число называется t-м числом Ферма. Например, пятое число Ферма равно

. Первые четыре числа Ферма являются простыми. Все по­следующие числа Ферма, по-видимому, являются составными. Когда модуль ранен числу Ферма, ТЧП реализуется для любого N, равного степени двойки и не превышающего , если число Ферма составное (т.е. начинается с F₅), а также для любого N , равного степени двойки и меньшего, чем М, если число Ферма простое (т.е. F₁ – F₄). В этом случае такие размеры преобразования позволяют использовать алгоритмы, подобные алгоритмам БПФ по основанию 2.

Арифметические операции по модулю F_t, могут быть выполнены с помощью b разрядных двоичных чисел. Количество разрядов, используемых для представления сигналов и коэффициентов фильтра (например, согласованного), определяет выбор значения b, которое необходимо использовать во избежание появления ошибок на вы­ходе из-за перевыполнения. Обычно значение b несколько больше удвоенного числа двоичных разрядов, используемых для представления сигналов. Если значение b, по­лученное из соображения отсутствия перевыполнения, не являются степень 2, то для того чтобы можно было использовать числа Ферма, его необходимо увеличить до ближайшей степени 2.

Прямое и обратное ТЧПФ последовательности длины N = 2^m определяются сле­дующим образом:

, ;

,

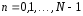
Заметим , что и . Теперь рассмотрим возможные значе­ния L, для которых существуют ТЧПФ.

Для простых чисел Ферма целое 3 является элементом поля порядка N = 2^b, допус­кающим наибольшую длину преобразования. Целое 2 имеет порядок N = 2^b = 2^t+1. Если 1, выбирается равным 2 или степени 2, то все степени L будут некоторыми степенями 2 и для таких случаев ТЧПФ может быть вычислено эффективно. Такое ТЧПФ (с базисной функцией L=2) называется преобразованием Рейдера. 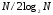Для вычисления такого N - точного преобразования, аналогичного БПФ требуется порядка сложе­ний—вычитаний и операций умножений на степень 2, которые выполняются путем поразрядных сдвигов с последующем вычитанием — значительно более быстрых операций, чем умножение. В итоге это может привести к сокращению объема вычисле­ний. Преобразование Рейдера обладает и другими преимуществами по сравнению с БНФ. Во-первых, в случае БПФ необходимо запоминать все степени V, что требует значительного объема Памяти. Это обстоятельство может оказаться существенным фактором при технической реализаций специализированных процессоров. Во-вторых, при вычислениях БПФ с фиксированной запятой на выходе вносится значительный по величине шум округления — 6-8 бит в зависимости от входных данных [4]. Это ухуд­шает отношение сигнал/шум при осуществлении операций фильтрации. В преобразованиях Рейдера шум округления отсутствует и единственным источником погрешности является преобразование аналог/цифра на входе.

Ограничение на применение этого преобразования связано с тем, что оно при­годно для вычислений сравнительно коротких сверток (последовательностей). На­пример, при использовании ТЧПФ и выборе b = 2, М = 2⁶⁴+1 длина преобразуемой по­следовательности N = 2^b = 128 и вычисления должны производиться с 64-ыми разряд­ными словами. Это создает определенные трудности для аппаратной и программной реализации обработки сигналов в реальном масштабе времени, т.к. существующие со­временные сумматоры, вычислители предполагают операции с 16- 12-битовыми сло­вами, что ведет к сокращению быстродействия, росту габаритных размеров процессо­ров цифровых фильтров, потребляемой мощности.