2.2.2. Вторая задача

Определение производительности проходческого комбайна с соосными роторами в породах с известными свойствами при заданных мощностях приводов отдельных механизмов.

Исходные данные:

сечение выработки – арочное;

площадь сечения S = 7,0 м²;

коэффициенты, определяющие затраты энергии: С₁ = 8·10⁵, С₂ = –0,4.

Параметры комбайна:

масса эксплуатационная m = 58000 кг;

механизм перемещения и подачи – гусеничный ход;

исполнительный орган – соосные буры;

механизм погрузки – ковшовый;

механизм формирования нижней части выработки – бермовые фрезы и отрезные коронки;

диаметр внешнего ротора – D₂ = 2,8 м;

диаметр центрального бура – D₁ = 2,0 м;

диаметр бермовых фрез – d₃ = 0,5 м;

диаметр отрезных коронок – d₄ = 0,5 м;

мощность двигателя привода соосных буров – 200 кВт;

мощность двигателя привода бермовых фрез и отрезных коронок – 110 кВт;

мощность двигателей привода гусениц – 2×20 кВт;

мощность двигателя привода конвейера – 10 кВт;

частоты вращения, об/мин:

– внешнего ротора п₂ = 8,0;

– центрального бура п₁ = 15,0;

– бермовых фрез п₃ = 20,0;

– отрезных коронок п₄ = 20,0.

Обоснование методики решения

Существуют несколько способов решения этой задачи, применение которых обуславливается, прежде всего, наличием исходных данных. Если, как в рассматриваемом примере, рассчитывается теоретическая производительность конкретного комбайна, то наиболее рациональная методика решения задачи следующая:

– составляется уравнение баланса мощности привода исполнительного органа (как правило, это наиболее нагруженный привод);

– из этого уравнения определяется теоретическая скорость подачи;

– по величине этой скорости определяются потребные мощности приводов всех остальных механизмов;

– полученные мощности сравниваются с мощностями установленных двигателей;

– если мощности двигателей не меньше определенных расчетом, то расчетная теоретическая скорость подачи принимается и по ее величине определяется теоретическая производительность;

– в противном случае теоретическая скорость подачи определяется из уравнения баланса мощности тех приводов, мощность двигателей которых недостаточна для обеспечения скорости подачи, определенной из уравнения баланса мощности основного исполнительного органа. За скорость подачи принимается наименьшая из них;

– по этой скорости и определяется теоретическая производительность.

Расчеты

Составление основного уравнения баланса мощности. Записываем уравнение баланса мощности привода центрального и внешнего буров, учитывая, что оба бура имеют общий привод,

, (54)

где N₁ – мощность для разрушения породы центральным буром;

N₂ – мощность для разрушения породы внешним ротором;

N_2и3 – мощность для зачерпывания породы ковшами и погрузки на конвейер;

η₁ и η₂ – КПД соответствующих приводов.

; (55)

– удельные затраты мощности на разрушение породы центральным буром;

 – площадь сечения, разрушаемая центральным буром;

v_n – скорость подачи;

– толщина стружки, снимаемой резцами центрального бура;

– число резцов в линии резания центрального бура;

b₁ = 0,05 м – ширина захвата резца центрального бура;

к₁ = 20 – общее число резцов центрального бура;

– угловая скорость центрального бура.

Вычисляем величины, необходимые для определения N₁:

м²;

рад/с;

;

;

.

Тогда

Вт.

Определяем N₂:

, (56)

где – удельные затраты мощности на разрушение породы внешним ротором;

– площадь сечения выработки, разрушаемая внешним ротором;

– толщина стружки, снимаемой резцами центрального бура;

– среднее число резцов в линии резания внешнего ротора;

b₂ = 0,05 м – ширина захвата резца внешнего ротора;

к₂ = 8 – общее число резцов внешнего ротора;

R₂ = 1,4 м – наружный радиус внешнего ротора;

– угловая скорость внешнего ротора.

м²;

рад/с;

;

;

.

Тогда

Вт.

Далее вычисляем мощность для погрузки породы на конвейер с учетом затрат энергии на зачерпывание породы ковшами

, (57)

где е₃ = 200000 Вт·с/м³ – удельные затраты энергии на зачерпывание породы ковшами;

h = 2,7 м – высота подъема породы ковшами.

= 1800000·v_n Вт.

Решение уравнения и его проверка

В окончательном виде уравнение баланса мощности привода соосных буров имеет вид

.

Принимаем КПД равным 0,75. Тогда

(58)

и окончательно с учетом значения N_д и вычисления правой части уравнения в киловаттах (кВт)

,

или

.

Приближенное решение этого уравнения м/с.

Производим проверку решения по уравнению баланса мощности привода соосных буров:

кВт,

что незначительно (на 2,3 %) выше, чем мощность двигателя N_д12 = 200 кВт. Погрешность в 2,3 % получена в результате округления приближенного значения скорости подачи в большую сторону. Примем значение скорости подачи, произведя округление до второй значащей цифры в меньшую сторону, т.е. м/с.

Проверим теперь, удовлетворяет ли определенная скорость подачи мощностям приводов остальных механизмов.

Привод бермовых фрез и отрезных коронок:

(59)

где е_р3 и е_р4 – удельные затраты мощности разрушения массива бермовыми фрезами и отрезными коронками, Вт·с/м³;

S₃ и S₄ – площади сечения, разрушаемые бермовыми фрезами и отрезными коронками, S₃ = 0,75 м²; S₄ = 0,12 м²;

f = 0,7 – коэффициент трения разрушаемой породы о почву выработки;

f₂ = 0,5 – коэффициент трения разрушаемой породы о лопасти бермовых фрез;

ω₃ – угловая скорость вращения бермовых фрез;

рад/с;

l = 0,7 м – средняя длина перемещения породы шнеками бермовых фрез;

η₃ и η₄ – КПД приводов бермовых фрез и отрезных коронок, η₃ = η₄ = 0,75.

Вычисляем е_р3 и е_р4, предварительно определив z₃ и z₄. Принимаем их равными значениям из предыдущего примера: z₃ = 1,5; z₄ = 1,6.

Тогда

= 2455000 Вт·с/м³; (60)

= 25195400 Вт·с/м³. (61)

Определяем теперь необходимую мощность двигателя привода бермовых фрез и отрезных коронок

= 18659 + 3100 + 2500 ≈ 24300 Вт = 24,3 кВт.

Полученное значение намного меньше установленной мощности двигателей по исходным данным.

Привод механизма перемещения и подачи. Мощность в рабочем режиме

, (62)

где – суммарное тяговое усилие гусеничных лент;

η = 0,7 – КПД привода гусениц;

ε = 0,05 – коэффициент буксования.

Сила сопротивления перемещению комбайна

. (63)

Значения μ = 0,03, k = 0,05 и φ = 12º принимаем как и в предыдущем примере.

При массе комбайна, равной 58000 кг,

Н.

Сила сопротивления подаче исполнительного органа

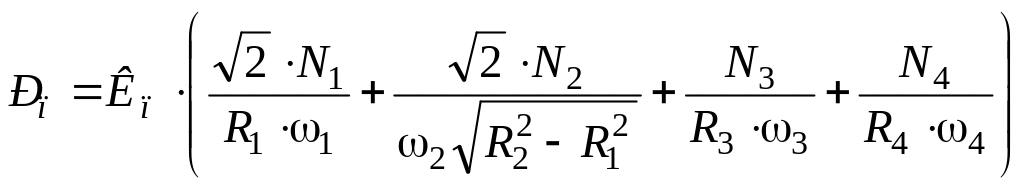, (64)

где К_п = 0,8 – коэффициент пропорциональности между силами сопротивления резанию и подаче;

– мощность для разрушения породы центральным буром;

– то же для внешнего бура;

– то же для бермовых фрез;

– то же для отрезных коронок.

Вт·с/м³,

Вт·с/м³,

Вт,

Вт,

Вт,

Вт,

= 125660 Н.

Крюковое усилие примем таким же, как и в предыдущем примере, Н. Тогда

Н,

а мощность для перемещения комбайна и подачи исполнительного органа на забой

кВт.

В транспортном режиме при скорости v_n = 180 м/ч

кВт.

Установленные двигатели обеспечивают требуемую мощность с большим запасом.

Проводим также проверку достаточности мощности двигателя привода ленточного конвейера:

, (65)

где Р_тк – окружное усилие на ведущем барабане;

v_б = 1,3 м/с – окружная скорость барабана;

η_к = 0,7 – КПД привода конвейера.

Величину Р_тк находим так же, как и в предыдущем примере:

. (66)

м/с; м; кг; К = 0,1; φ = 12º;

кг/с.

Н.

Вт = 5,8 кВт.

Установленный двигатель с запасом обеспечивает работу конвейера.

Вывод: комбайн может работать в породах с заданными свойствами с теоретической скоростью подачи 0,0076 м/с, что дает теоретическую производительность Q = 7·0,0076 = 0,053 м³/с.