2. Явление теплопроводности. Коэффициент теплопроводности.

Теплопрово́дность — способность материальных тел к переносу энергии (теплообмену) от более нагретых частей тела к менее нагретым телам, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналогпроводимости.

Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В системе СИ единицей измерения коэффициента теплопроводности является Вт/(м·K).

Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.

КОЭФФИЦИЕНТ ТЕПЛОПРОВОДНОСТИ

величина, характеризующая теплопрово - дящие свойстваматериала и определяемая плотностью теплового потока при единичной разности температур междуповерхностями слоя материала единичной толщины

еплопроводность представляет собой процесс распространения тепла путем непосредственного соприкосновения беспорядочно движущихся (колеблющихся) структурных частиц вещества – молекул, атомов, электронов. Это так называемый молекулярный способ переноса тепловой энергии, который может осуществляться в любых термически неравновесных (т.е. имеющих различные температуры) телах или системах тел.

В основу теории теплопроводности положен закон Фурье – тепловой поток прямо

пропорционален температурному градиенту:

(2.1)

,

где Н – площадь поверхности, через которую проходит тепло, [м²];

- коэффициент теплопроводности;

- температурный градиент, [К/м], [^oC/м].

Коэффициент теплопроводности характеризует способность тел проводить тепло:

(2.2)

.

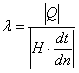По своему физическому смыслу коэффициент теплопроводности представляет собой количество тепла, проходящего в единицу времени через единицу изотермической поверхности при температурном градиенте, равном единице, или другими словами, это тепловой поток в единицу времени через единицу изотермической поверхности при изменении температуры на единицу толщины стенки в один градус. Коэффициент теплопроводности зависит от природы тела, его пористости, влажности, давления, температуры и других параметров. Для всех материалов с изменением температуры λ изменяется по линейному закону во всем рассматриваемом интервале температур:

(2.3)

,

где λо – коэффициент теплопроводности при 0 ^оС;

b – постоянная, характеризующая приращение (уменьшение) λ материала при повышении его температуры на 1 ^оС.

Численное значение коэффициента теплопроводности определяется опытным путем различными методами (шара, плиты и др). Для теплоизоляционных материалов ( λ ≤ 0,3 [Вт/м·К]) наибольшее распространение получил метод трубы (цилиндра), сущность которого заключается в следующем.

При установившемся тепловом режиме количество тепла Q, передаваемого в единицу времени от внутренней поверхности цилиндра к наружной на участке длиной L, определяется согласно закону Фурье для цилиндрической стенки:

(2.4)

.

Установившийся (стационарный) режим предполагает неизменность температур t₁ и t₂ на внутренней и внешней поверхностях стенки диаметром, соответственно d₁ и d₂ (см. рис. 3.4), в различные моменты времени.

Таким образом, если коэффициент теплопроводности рассматривать как постоянную в диапазоне температур t₁-t₂ величину, то измерив значения t₁, t₂, Q, его можно вычислить из уравнения

(2.5)

.

БИЛЕТ №3

1. Скорость движения материальной точки. Мгновенная скорость. Ускорение. Их проекции на координатные оси. Уравнения движения. Ускорение при криволинейном движении: тангенциальное и нормальное ускорения.

Ско́рость (часто обозначается  , от англ. velocity или фр. vitesse, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени^[1]. Этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, т. е. проекцию этого вектора на касательную к траектории точки^[2].

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.

Обобщениями понятия скорости является четырёхмерная скорость, или скорость в релятивистской механике, и обобщённая скорость, или скорость в обобщённых координатах.

Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.

Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.

Ускоре́ние (обычно обозначается латинскими буквами a (от лат. acceleratio) или w) — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости   тела при его движении за единицу времени:

Например, тела, свободно падающие вблизи поверхности Земли в вертикальном направлении, в случаях, когда испытываемое имисопротивление воздуха мало, увеличивают свою скорость примерно на 9,8 м/с каждую секунду, то есть их ускорение примерно равно 9,8 м/с².

Важно, что ускорение является вектором, то есть учитывает не только изменение величины скорости (модуля векторной величины), но и изменение её направления. В частности, ускорение тела, движущегося по окружности с постоянной по модулю скоростью, не равно нулю; тело испытывает постоянное по модулю (и переменное по направлению) ускорение, направленное к центру окружности (центростремительное ускорение).

Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s², м/с²), существует также внесистемная единица гал (gal), применяемая в гравиметрии и равная 1 см/с².

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

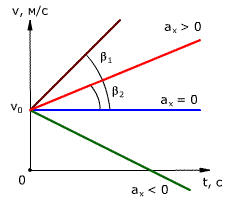  Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

  Рис. 1.18. Зависимость перемещения тела от времени.

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

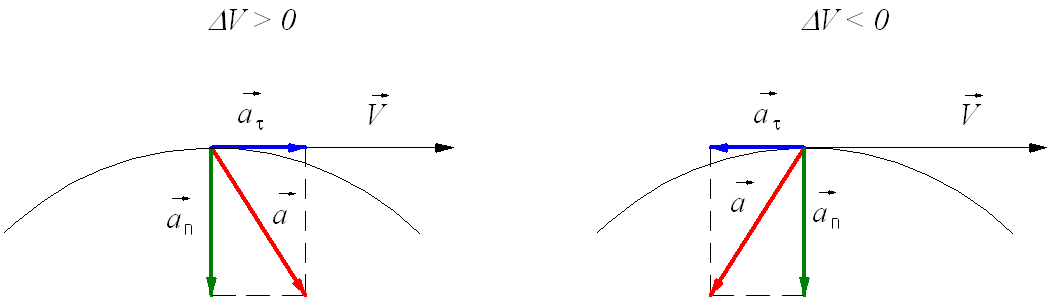Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  _τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой  _n. Вектор нормального ускорения направлен по радиусу кривизны траектории.