2. Понятие адиабатного процесса. Уравнение Пуассона. Показатель адиабаты идеального газа.

АДИАБАТНЫЙ ПРОЦЕСС

Адиабатный процесс — процесс, при котором отсутствует теплообмен между системой и окружающей средой.

Из первого начала термодинамики следует, что работа газа при адиабатном процессе совершается за счет его внутренней энергии:  (1). С другой стороны, из уравнения Клапейрона-Менделеева следует:  (2). Разделим уравнение (2) на уравнение (1): , где . Проинтегрируем полученное уравнение: . Таким образом, при адиабатном процессе  или   — уравнение Пуассона. С учетом уравнения Клапейрона-Менделеева ( , ) уравнение Пуассона может быть представлено в виде:  или   или  .

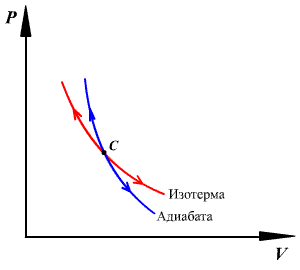График адиабатного процесса — более крутая кривая, чем гипербола при изотермическом процессе. Это следует из выражения производной  , полученной из уравнения Пуассона.

Работа газа при адиабатном процессе равна убыли внутренней энергии: .

Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством.  Серьёзное исследование адиабатических процессов началось в XVIII веке^[1].

Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна^[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётсяравновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы^[3].

Адиабата Пуассона[

Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением^[6][15][16]

где   — его объём,   — показатель адиабаты,   и   — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

График адиабаты (жирная линия) на  диаграмме для газа.  — давление газа;  — объём.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

где   — абсолютная температура газа. Или к виду

Поскольку   всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении  ) газ нагревается (  возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент  .

Вывод уравнения[править | править вики-текст]

Согласно закону Менделеева — Клапейрона^[6] для идеального газа справедливо соотношение

где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обеих частей уравнения, полагая независимыми термодинамическими переменными  , получаем

(3)

Если в (3) подставить   из (2), а затем   из (1), получим

или, введя коэффициент  :

.

Это уравнение можно переписать в виде

что после интегрирования даёт:

.

Потенцируя, получаем окончательно:

что и является уравнением адиабатического процесса для идеального газа.

Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении ( ) к теплоёмкости при постоянном объёме ( ). Иногда его ещё называют фактором изоэнтропийного расширения. Обозначается греческой буквой   (гамма) или   (каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква  ^[1].

Уравнение:

,

где

 — теплоёмкость газа,

 — удельная теплоёмкость (отношение теплоёмкости к единице массы) газа,

индексы   и   обозначают условие постоянства давления или постоянства объёма, соответственно.

БИЛЕТ 9