20

Тема 3. Множественная регрессия и корреляция

На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Например, спрос на некоторый товар определяется не только ценой данного товара, но и ценами на замещающие и дополняющие товары, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии рассматривается множественная регрессия

(1)

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и в ряде других вопросов экономики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике.

Основной целью множественной регрессии является построение модели с большим числом факторов, а также определение влияния каждого фактора в отдельности и совокупного их воздействия на моделируемый показатель.

Включение в уравнение множественной регрессии того или иного набора факторов связано, с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. они должны быть количественно измеримы (качественные показатели могут быть проранжированы);

2. факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной зависимости.

Множественный корреляционный и регрессионный анализ

Корреляционный анализ обычно предшествует регрессионному анализу.

Анализ матрицы парных коэффициентов корреляции

Матрица состоит из коэффициентов парной корреляции, рассчитанных для набора переменных y, x₁, x₂,….., x_m и размещенных в виде матрицы. Переменная y называется зависимой, а остальные x₁, x₂,….., x_m независимыми.

Так как r_xy = r_yx, то корреляционная матрица симметрична относительно главной диагонали, поэтому естественно анализировать только одну из частей корреляционной матрицы (верхнюю или нижнюю относительно главной диагонали).

Корреляционная матрица R имеет вид:

y x₁ x₂ … x_m

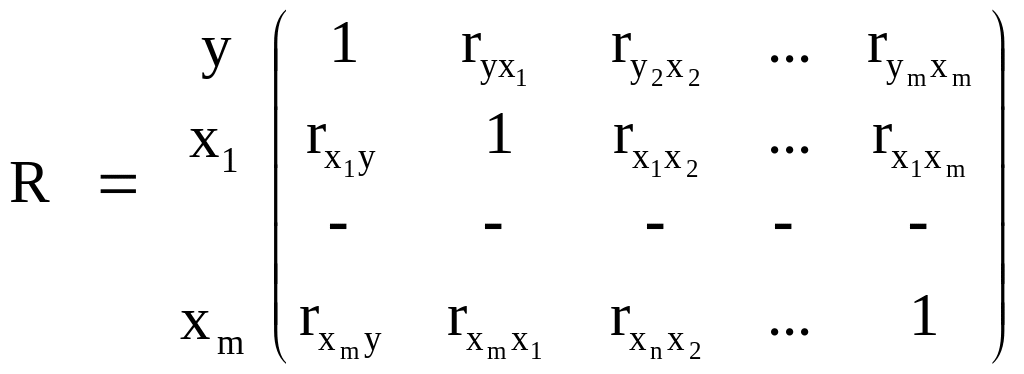
Первая строка матрицы содержит коэффициенты корреляции между зависимой переменной y и независимыми переменными х₁, х₂, …, x_m. Коэффициенты этой строки анализируют с целью выявления значимых независимых переменных. Значимость независимой переменной здесь понимается с точки зрения влияния ее на зависимую переменную. Если проверка гипотезы Н₀: = 0 покажет, что коэффициент корреляции между y и x_i не значимо отличен от нуля, то это означает, что соответствующая независимая переменная незначима, и в уравнение регрессии ее включать не следует. Подобные выводы правомерны лишь на начальном этапе анализа информации.

Второй этап анализа матрицы парных коэффициентов корреляции заключается в выявлении мультиколлинеарности среди независимых переменных.

Мультиколлинеарность – это наличие линейной зависимости между независимыми переменными (факторами х) в регрессионной модели. При этом различают полную коллинеарность, которая означает наличие функциональной (тождественной) линейной зависимости и частичную или просто мультиколлинеарность — наличие сильной корреляции между факторами.

Полная коллинеарность приводит к неопределенности параметров в линейной регрессиионной модели независимо от методов оценки.

Идеальным условием реализации регрессионного анализа является независимость между собой независимых переменных.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Включаемые во множественную регрессию факторы, должны объяснить вариацию независимой переменной.

Если строится модель с набором факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака у за счет рассматриваемых в регрессии факторов.

Влияние других, не учтенных в модели факторов, оценивается как с соответствующей остаточной дисперсией .

Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы.

Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение при этом отдается, который при достаточно тесной связи с результатом у имеет наименьшую тесноту связи с другими факторами.

Пусть, например, при изучении зависимости матрица парных коэффициентов корреляции оказалась следующей:

	1	0,8	0,7	0,6
	0,8	1	0,8	0,5
	0,7	0,8	1	0,2
	0,6	0,5	0,2	1

Очевидно, что факторы и дублируют друг друга.

В анализ целесообразно включить фактор , а не , хотя корреляция с результатом слабее, чем корреляция фактора с , но зато значительно слабее межфакторная корреляция . Поэтому в данном случае в уравнение множественной регрессии включаются факторы , .

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

1. Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде; параметры линейной регрессии теряют экономический смысл.

2. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений, что делает модель непригодной для анализа и прогнозирования.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

1. Метод исключения – отсев факторов из полного его набора.

2. Метод включения – дополнительное введение фактора.

3. Шаговый регрессионный анализ – исключение ранее введенного фактора.

При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия.

Как и в парной зависимости возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции (степенная легко линеаризуется).

Ввиду четкой интерпретации параметров наиболее широко используется линейная функция.

В линейной множественной регрессии параметры при называются коэффициентами «чистой» регрессии.

Коэффициенты «чистой» регрессии характеризуют среднее изменение результата у с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

.

Пример. По предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов ( от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих ( ).

Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:

№
1	2	3	4	5	6	7	8	9	10
1	7,0	3,9	10,0	27,3	70,0	39,0	15,21	100,0	49,0
2	7,0	3,9	14,0	27,3	98,0	54,6	15,21	196,0	49,0
3	7,0	3,7	15,0	25,9	105,0	55,5	13,69	225,0	49,0
4	7,0	4,0	16,0	28,0	112,0	64,0	16,0	256,0	49,0
5	7,0	3,8	17,0	26,6	119,0	64,6	14,44	289,0	49,0
6	7,0	4,8	19,0	33,6	133,0	91,2	23,04	361,0	49,0
7	8,0	5,4	19,0	43,2	152,0	102,6	29,16	361,0	64,0
8	8,0	4,4	20,0	35,2	160,0	88,0	19,36	400,0	64,0
9	8,0	5,3	20,0	42,4	160,0	106,0	28,09	400,0	64,0
10	10,0	6,8	20,0	68,0	200,0	136,0	46,24	400,0	100,0
11	9,0	6,0	21,0	54,0	189,0	126,0	36,0	441,0	81,0
12	11,0	6,4	22,0	70,4	242,0	140,8	40,96	484,0	121,0
13	9,0	6,8	22,0	61,2	198,0	149,6	46,24	484,0	81,0
14	11,0	7,2	25,0	79,2	275,0	180,0	51,84	625,0	121,0
15	12,0	8,0	28,0	96,0	336,0	224,0	64,0	784,0	144,0
16	12,0	8,2	29,0	98,4	348,0	237,8	67,24	841,0	144,0
17	12,0	8,1	30,0	97,2	360,0	243,0	65,61	900,0	144,0
18	12,0	8,5	31,0	102,0	372,0	263,5	72,25	961,0	144,0
19	14,0	9,6	32,0	134,4	448,0	307,2	92,16	1024,0	196,0
20	14,0	9,0	36,0	126,0	504,0	324,0	81,0	1296,0	196,0
Сумма	192	123,8	446	1276,3	4581	2997,4	837,74	10828,0	1958,0
Ср. знач.	9,6	6,19	22,3	63,815	229,05	149,87	41,887	541,4	97,9

1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

Вычисление параметров линейного уравнения множественной регрессии.