Лаба 1-8 Лабы и ПЗ [Вариант 1] / 5 / 7цос

Белорусский государственный университет

информатики и радиоэлектроники

Кафедра радиотехнических систем

Отчет

по лабораторной работе №7

“ Теоретико-числовые преобразования ”

Выполнил: Проверил:

Студент гр. 740101 Ходыко Д.Л

Дрягин Д.В

Минск 2010

Цель работы:

Изучение алгоритмов цифровой обработки сигналов на основе теоретико-числовых преобразований в конечном поле или кольце целых чисел по модулю чисел Ферма и по методу чисел Мерсенна.

Предварительное задание

а)N=5 – число отсчетов, a=2 – основание , S(n) = {-1,1,-1, -1,1}

b). N=7, a=2, S(n) = {-1,1,-1,-1,1,1,1}

Решение:

1) Определить модуль, с которым будет выполняться прямое и обратное теоретико-числовые преобразования.

a)

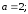
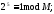
Условие выполнения обратного теоретико-числового преобразования: элементы и должны существовать в кольце целых чисел по модулю М. Проверим, выполнение данного условия

Для операции сложения:

Для операции умножения:

Ответ: M=31.

b)

Операция сложения:

Операция умножения:

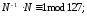
Ответ:M=127.

2) Построить прямую и обратную матрицу ТЧП для заданных параметров

a) Для построения матрицы прямого теоретико-числового преобразования воспользуемся следующими соотношениями:

Матрица обратного теоретико-числового преобразования имеет вид:

b) Для построения матрицы прямого теоретико-числового преобразования воспользуемся следующими соотношениями:

Матрица обратного теоретико-числового преобразования имеет вид:

3)Вычислить прямое и обратное ТЧП для последовательностей

а)

Перейдем к вычислению коэффициентов прямого теоретико-числового преобразования.

б)

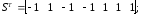
Вычислим коэффициенты прямого теоретико-числового преобразования.

4) Найти четырехточечную циклическую свертку последовательности (1, 2, 0, 0) саму с собой с помощью графа быстрого ТЧП.

Выполнение

1)Выбор параметров:

элемент ТЧП а=2

Длина(размерность) N=4

, то M=15

2)Формирование матрицы ТЧП

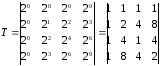
4)Вычисление свертки

2 элемент ТЧП для {S(n)} 0mod15=0

5) Быстрое ТЧП

S(n)={0,1,-1,3}

6) Последовательность S(n) после двоично-инверсной перестановки

7)Последовательность после первой итерации

8)Последовательность после второй итерации

9)Последовательность после возведения в квадрат,умножение на число обратное N

и изменения знака степени

10) Последовательность S(n) после двоично-инверсной перестановки

11)Последовательность после первой итерации

Вывод: в этой работе исследовались теоретико-числовые преобразования. Было изучено какими преимуществами ТЧП обладают перед обычными БПФ, а также о недостатках ТЧП; основные свойства базисных функций и теоретико-числового преобразо­вания; преобразования с числами Ферма и Мерсенна; быстрое вычисление свертки с помощью теоретико-числового преобразования Ферма