
Лаба 1-8 Лабы и ПЗ [Вариант 1] / 1 / laba#1 с предварительным заданием
.pdfБелорусский государственный университет информатики и радиоэлектроники
Кафедра радиотехнических систем
О Т Ч Ё Т
по лабораторной работе по курсу “Цифровая обработка сигналов”
на тему
“Линейные дискретные системы”
Выполнил: |
Проверил: |
студент ФРЭ, гр. 742801 |
доц. каф. РТС |
Борисенко Сергей Юрьевич |
Семашко Павел Геннадьевич |
Минск 2010

1.Цели работы
а) исследование разностных уравнений и Z-преобразований
б) ознакомление со средой математического моделирования MATLAB в) моделирование линейных дискретных систем в MATLAB
2.Домашнее задание
а) вычислить Z-преобразование от y[n]
б) по заданной передаточной характеристике H[z] записать разностное уравнение и определить первые шесть значений импульсной характеристики
Разностное уравнение получено. Теперь подадим на вход устройства воздействие типа дельта-функции 





 :
:

в) по заданной передаточной характеристике построить схему цифрового фильтра
Рис. 1. Схема цифрового БИХ-фильтра

г) по разностному уравнению определить передаточную характеристику, а также определить реакцию фильтра на входное воздействие x[n]=2n
Для отыскания реакции фильтра на заданное воздействие, определим несколько отсчетов импульсной характеристики, а затем, по известной формуле свертки
определим реакцию у[n].
Отсчеты импульсной характеристики:
Применяем формулу свертки:
Видим, что полученные значения можно свести к формуле:
Это и есть искомая реакция фильтра.

3. Экспериментальная часть, выполненная в MATLAB
ВАРИАНТ 7. БИХ-фильтр верхних частот.
Частота дискретизации Частота среза Вектор воздействия:
Вектор реакции:
Фазовые величины:
a) Вычисление импульсной характеристики путем воздействия дельта-функцией Код для MATLAB:
b=[0.012 -0.123 0.555 -1.479 2.588 -3.106 2.588 -1.479 0.555 -0.123 0.012]; a=[1 -1.872 3.428 -2.78 2.663 -0.909 0.881 -0.06 0.375 -0.06 0.132]; N=length(b);
delta=[1;zeros(N, 1)]; h=filter(b,a,delta); stem(0:N-1,h)
grid
Рис. 2. Импульсная характеристика
b) Вычисление импульсной характеристики по отсчетам разностного уравнения Код для MATLAB:
b=[0.012 -0.123 0.555 -1.479 2.588 -3.106 2.588 -1.479 0.555 -0.123 0.012]; a=[1 -1.872 3.428 -2.78 2.663 -0.909 0.881 -0.06 0.375 -0.06 0.132];
N=50;
Fs=48000;
[h,nT]=impz(b,a,N,Fs);
stem(nT,h), grid

Рис. 3. Импульсная характеристика, вычисленная по отсчетам РУ
c)Вычисление реакции ЛДС на входное воздействие на основе разностного уравнения. В качестве входного воздействия использовать сумму двух гармонических колебаний. Амплитуды двух колебаний принять равными 1В
Код для MATLAB:
b=[0.012 -0.123 0.555 -1.479 2.588 -3.106 2.588 -1.479 0.555 -0.123 0.012]; a=[1 -1.872 3.428 -2.78 2.663 -0.909 0.881 -0.06 0.375 -0.06 0.132]; n=0:32;
x=sin(0.982*n)+sin(0.524);
y=filter(b,a,x); plot(n,x,'-or', n,y,'-ob') grid
hold on stem(n,x, '-or') stem(n,y)
gtext('Output signal') gtext('Input signal')
Рис. 4. Реакция ЛДС на сумму гармонических колебаний

d)Вычислить реакции ЛДС на основе уравнения свертки. В качестве входного воздействия использовать сумму двух гармонических колебаний. Амплитуды двух колебания принять равными 1В
Код для MATLAB:
b=[0.012 -0.123 0.555 -1.479 2.588 -3.106 2.588 -1.479 0.555 -0.123 0.012]; a=[1 -1.872 3.428 -2.78 2.663 -0.909 0.881 -0.06 0.375 -0.06 0.132]; delta=[1;zeros(50,1)];
h=filter(b,a,delta);
n=0:50;
x=sin(0.982*n)+sin(0.524);
y=conv(x,h);
k=length(y); stem(0:k-1,y),grid
Рис. 5. Реакция ЛДС на основе уравнения свертки
e) Рассчитать АЧХ и ФЧХ фильтра и построить графики
Код для MATLAB:
b=[0.012 -0.123 0.555 -1.479 2.588 -3.106 2.588 -1.479 0.555 -0.123 0.012]; a=[1 -1.872 3.428 -2.78 2.663 -0.909 0.881 -0.06 0.375 -0.06 0.132]; N=length(a)*10
h=impz(b,a,N); Ah=fft(h,N); H=abs(Ah); ph=angle(Ah); dl=round(N/2); H=H(1:dl); ph=ph(1:dl); n=0:dl-1;
plot(n,H,'-or',n,ph,'-ob'); grid
Рис. 6. АЧХ и ФЧХ фильтра

f)собрать КИХ-фильтр 4-го порядка, определить импульсную и частотную характеристики фильтра
Рис. 7. КИХ-фильтр 4-го порядка
Рис. 8. Импульсная и частотная характеристики КИХ-фильтра
g)собрать БИХ-фильтр по передаточной характеристике из пункта 2б, определить импульсную и частотную характеристики фильтра.
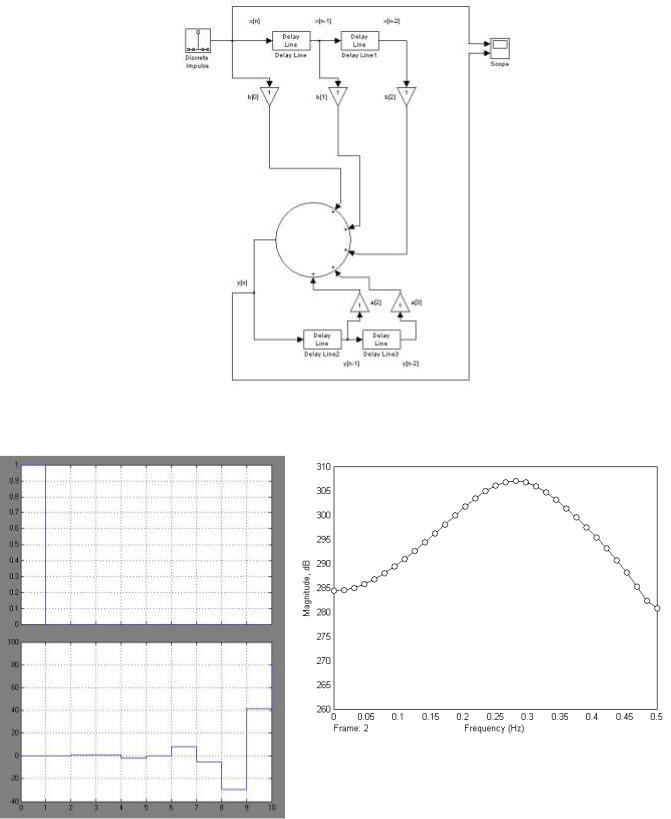
Рис. 9. БИХ-фильтр
Рис. 10. Импульсная и частотная характеристики БИХ-фильтра
4.Выводы
Вработе производились исследования линейных дискретных систем с помощью MATLAB. Были изучены основные характеристики КИХ- и БИХ-фильтров, теоретически определены математические выражения, описывающие работу конкретных фильтров. Результаты, полученные экспериментально, подтверждаются соответствующими сведениями из теории ЛДС.
