Примеры решения задач по физике (3часть) Геометрическая оптика

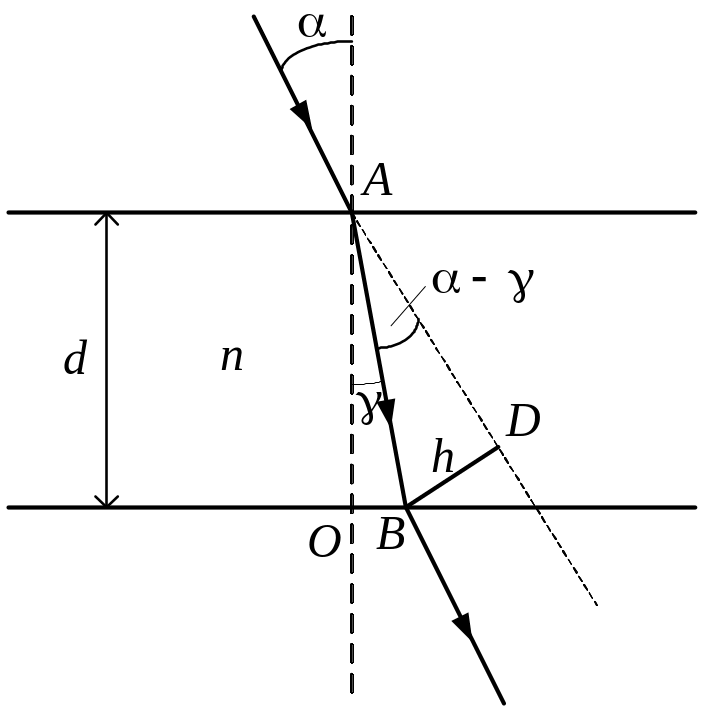
Задача 3.1

На плоскопараллельную стеклянную пластинку толщиной = 8 см падает под углом = 60° луч света. Определить боковое смещение луча , прошедшего сквозь эту пластинку.

Дано: = 8∙10–2 м = 60°	Решение Вышедший из пластинки луч будет параллелен падающему, т.е. плоскопараллельная пластинка не изменяет направление падающих на нее лучей, а только смещает их относительно первоначального хода.
– ?

Это смещение и надо определить.

Из (см. рис.)

. (1)

Из найдем:

. (2)

Подставляя (2) в (1), получим:

. (3)

Угол найдем, используя закон преломления:

;

;

;

.

Подставив числовые значения в формулу (3), получим:

.

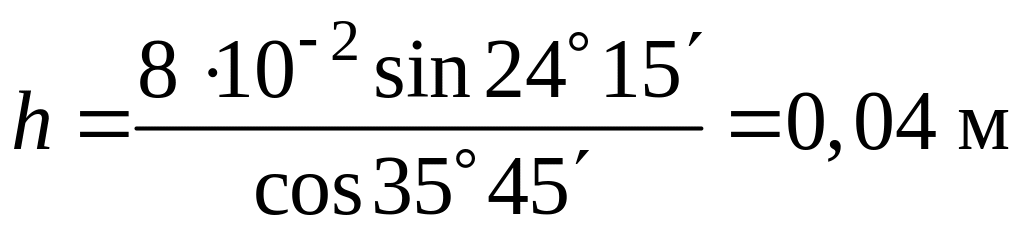Ответ: .

Задача 3.2

Наблюдатель рассматривает светящуюся точку через плоскопараллельную стеклянную пластину с показателем преломления 1,5 толщиной 3 см так, что луч зрения нормален к пластине. Определить расстояние между светящейся точкой и ее изображением (см. рис.).

Дано: = 1,5 = 3∙10–2 м	Решение В глаз наблюдателя попадает световой пучок, лучи которого образуют между собой весьма малые углы. Продолжения этих лучей пересекаются в одной
– ?

точке , являющейся изображением светящейся точки . Пусть два луча выходят из точки и попадают в глаз. Один из них, луч , падает нормально на пластинку. Другой луч попадает под произвольным весьма малым углом . Этот луч, дважды преломившись, выйдет из пластинки параллельно отрезку .

Чтобы определить положение точки , в которой пересекутся продолжения этих двух лучей, проведем отрезок , параллельный лучу .

Из параллелограмма следует:

.

П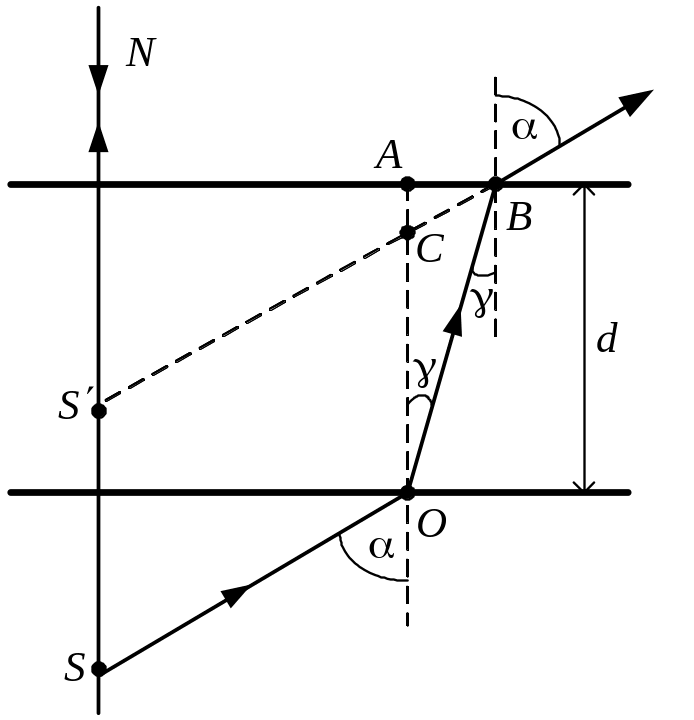 ри этом отрезок можно выразить через толщину пластинки и ее показатель преломления . Для этого заметим, что если бы в точке находился источник света, его изображением явилась бы точка , так как здесь пересекались бы лучи, выходящие из точки , после преломления на верхней грани пластинки:

.

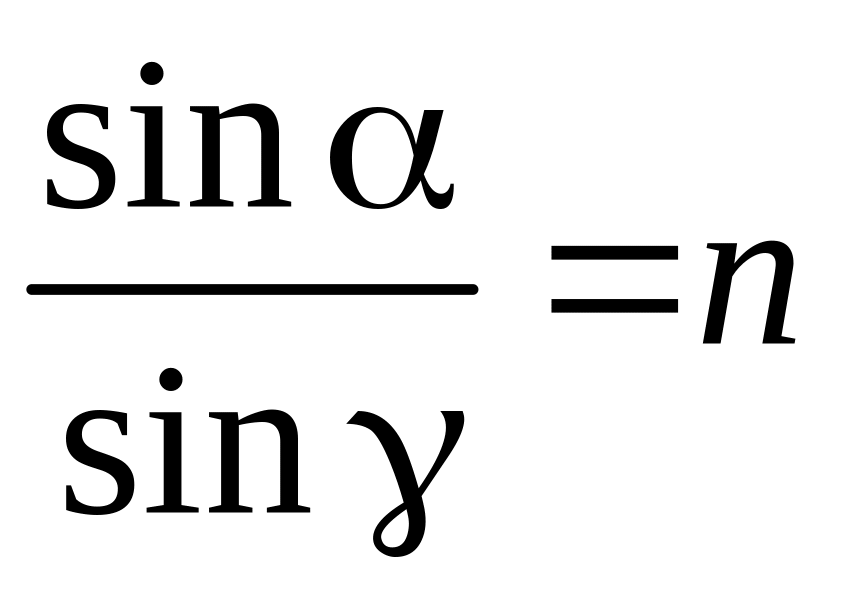Из треугольника

,

из треугольника

,

тогда получим:

.

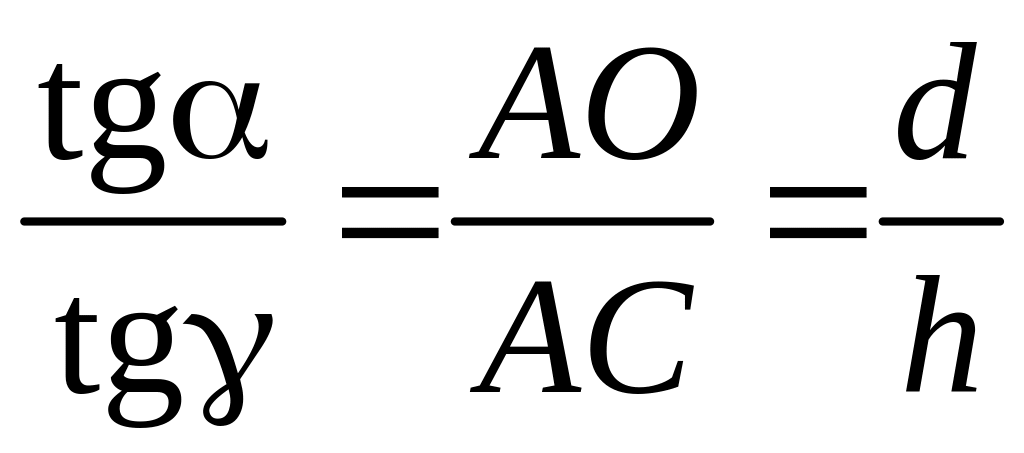Так как углы малы, то

.

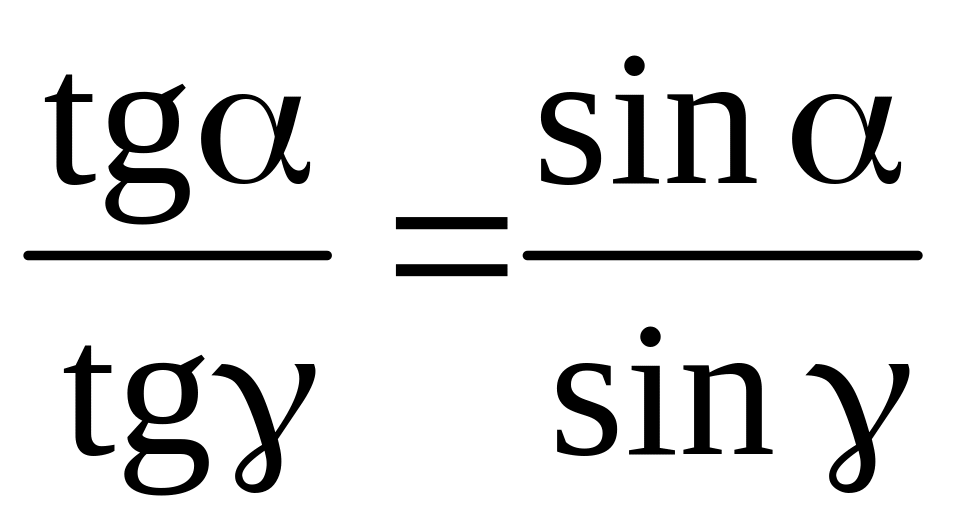Следовательно,

; .

Отсюда

;

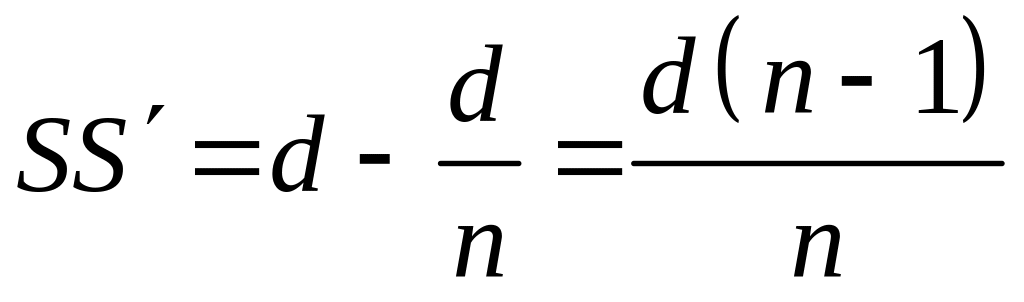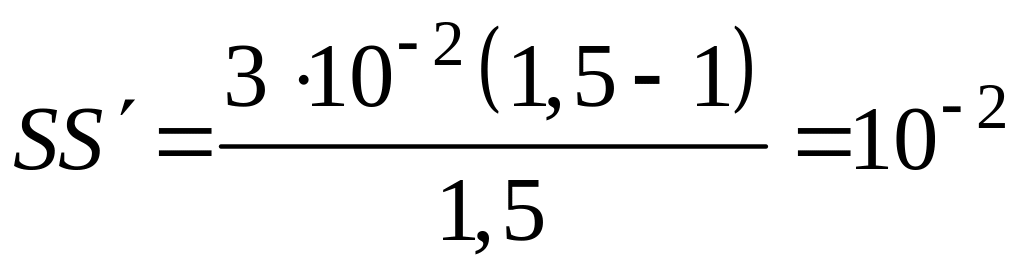м.

Изображение смещено относительно светящейся точки на 1 см в сторону наблюдателя.

Ответ: м.

Задача 3.3

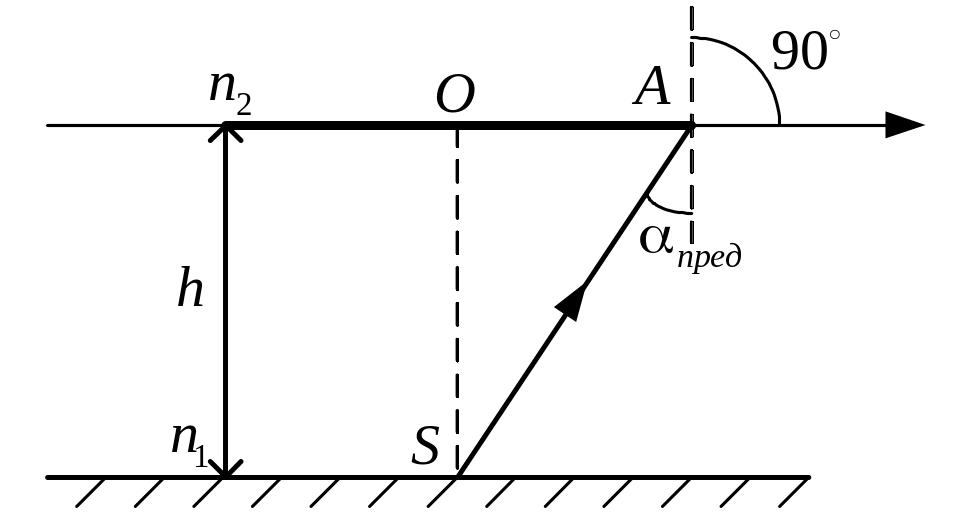
На дно сосуда, наполненного скипидаром до высоты 10 см, помещен источник света . На поверхности скипидара плавает круглая непрозрачная пластина так, что ее центр находится над источником света. Какой наименьший радиус должна иметь эта пластинка, чтобы ни один луч не мог выйти из скипидара (см. рис.)? Определить скорость света в скипидаре.

Дано: м м/с	Решение Луч света идет из среды более оптически плотной (скипидар) в менее плотную среду (воздух). При угле падения, равном предельному, угол преломления будет равен 90°. При угле падения больше луч будет отражаться от границы раздела (полное внутреннее отражение);
– ?

;

.

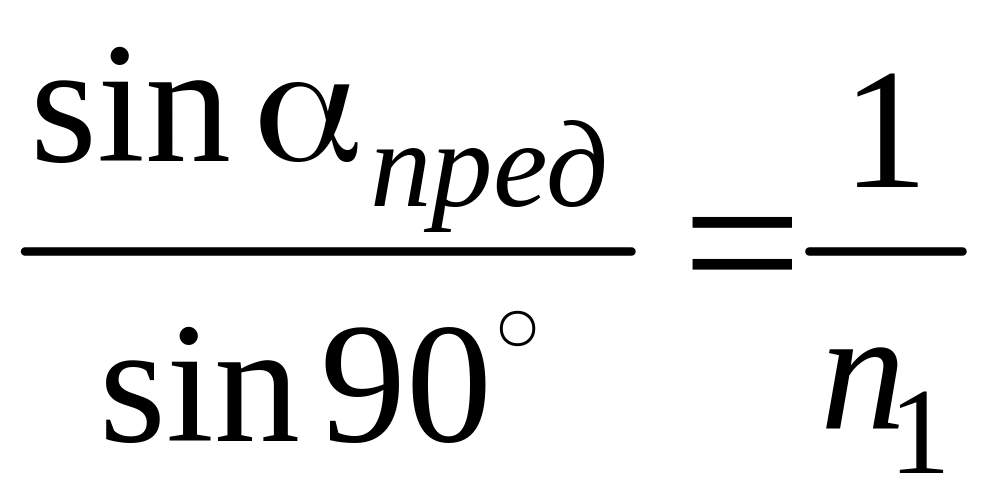
Тогда из треугольника можно определить при :

;

;

.

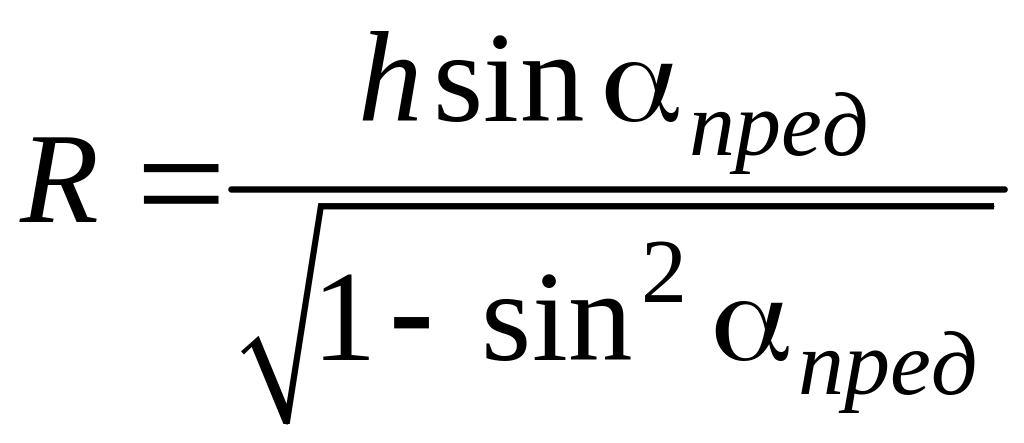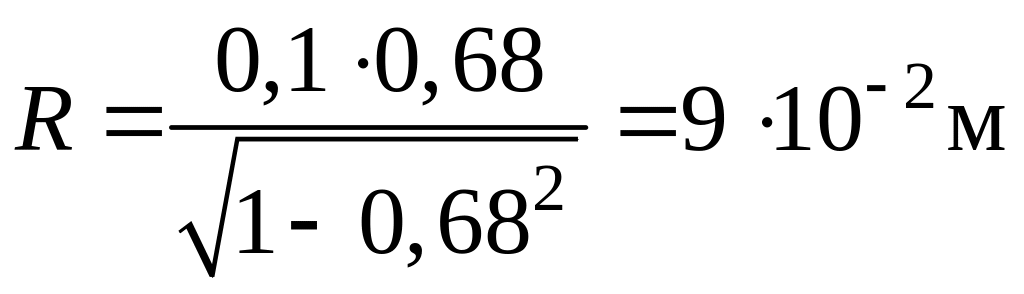Для определения скорости света в скипидаре воспользуемся соотношением

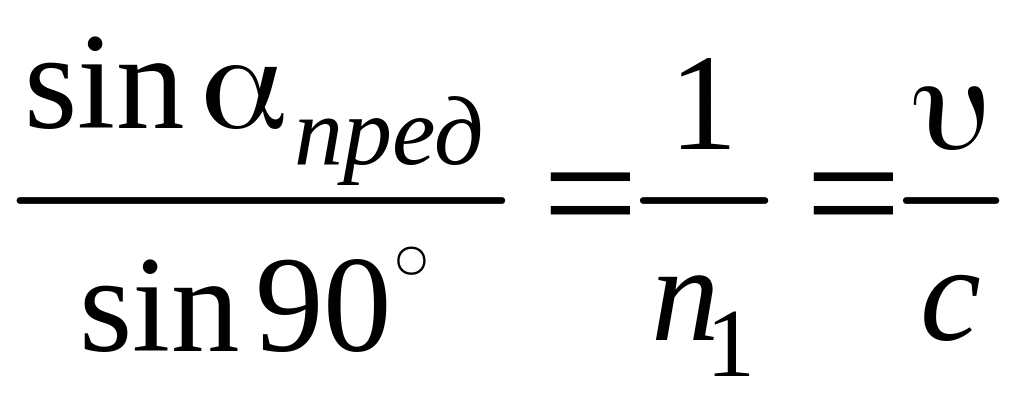; отсюда 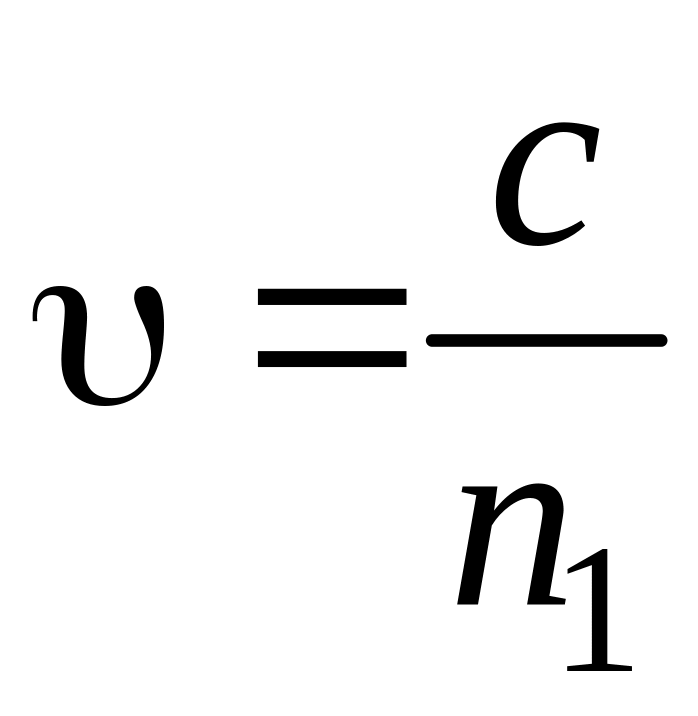; 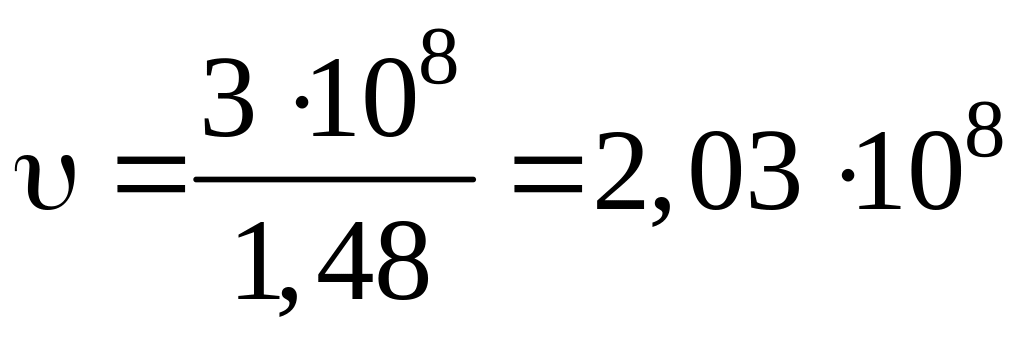м/с.

Ответ: ; м/с.