2.10.Особенности проектирования балок замкнутого сечения.

По конфигурации сечения различают балки с открытым и замкнутым профилями.

Балки замкнутого сечения обладают рядом преимуществ по сравнению с открытыми:

-более высокая несущая способность конструкции или ее элементов при работе на изгиб в двух плоскостях и на кручение. Материал в замкнутых сечениях располагается в основном в периферийных зонах по отношению к центру тяжести, что обусловливает увеличение моментов инерции и сопротивления относительно оси «у» (из плоскости элемента), и момента инерции на кручение;

- жесткость на кручение балок в большой степени зависит от того, является поперечное сечение балки открытым или замкнутым; открытые профили имеют гораздо меньшую крутильную жесткость, чем замкнутые, и могут получить гораздо большую депланацию, т. е. неравномерные по сечению продольные перемещения точек, принадлежащих первоначально плоским поперечным сечениям. Вследствие существенного увеличения (в десятки раз) момента инерции на кручение в элементах с замкнутыми сечениями, как правило, исключается изгибно-крутильная форма потери устойчивости;

-элементы с замкнутыми сечениями более устойчивы при монтаже, менее подвержены механическим повреждениям во время транспортировки и монтажа.

Так как изгибающие моменты, действующие во взаимно перпендикулярных плоскостях, как правило, неодинаковы, наиболее часто применяют балки прямоугольного коробчатого сечения. При приблизительном равенстве изгибающих моментов целесообразно использовать трубчатое сечение.

Недостаточно широкое применение балок замкнутого сечения объясняется прежде всего низкой технологичностью и, как следствие, большой трудоемкостью изготовления.

Замкнутые, в частности коробчатые, сечения применяют при необходимости увеличения жесткости балки в поперечном направлении, при отсутствии поперечных связей, изгибе в двух плоскостях, наличии крутящих моментов, при ограниченной строительной высоте и больших поперечных силах. Подобным силовым воздействиям при названных конструктивных ограничениях подвергаются балочные конструкции мостов, силовых элементов промышленных сооружений, кранов и др.

Коробчатые балки работают, как правило, в условиях сложного сопротивления, воспринимая шесть внутренних сил: продольную N, поперечные

Q _x и Q_y, изгибающие моменты М _х и М _у, крутящий момент М _КР (рис.2.31). В

y

.A

.B

Q_y . C

.D

M_y

N Q_x .

E

x

z M_x

Рис.2.31.Схема нагружения коробчатых балок

сечении появляются нормальные σ_N, σ_Mx и σ_{М у} и касательные τ _Qx, τ _Qy , τ _{М кр} напряжения, неравномерно распределенные по сечению. При этом максимальные напряжения действуют в точках внешнего контура (рис.2.32 ).

Прочность оценивают по эквивалентным напряжениям ( по гипотезе упругой энергии формоизменения)

σ _ЭКВ = σ ² + 3τ² , (2.19)

N M_X y M_y x

г де σ = ± ± ± - суммарные нормальные напряжения;

F J_X J_y

τ = ± τ _Qx ± τ _Qy ± τ _{М кр} – суммарное касательное напряжение.

При расчете по существующим методикам нередко допускают неточность, заключающуюся в том, что в условие (2.19) подставляют максимальные значения напряжений σ и τ, не учитывая, что они имеют место в разных точках сечения. Действительно, σ = σ _max в одной из угловых точек, а τ = τ _max – в одной из точек внешнего контура, лежащих на оси симметрии сечения. Такой расчет недопустим, так как ошибка, идущая в запас прочности, может быть существенной, что приведет к неоправданному увеличению массы конструкции. Желательно рассчитывать σ _ЭКВ для множества точек внешнего

у

τ_{Q y}

τ_Qx

τ_{M кр}

x x

τ _{М кр} τ_Qy τ _Qx

y Q _y y

М_кр

x x x х

Q_x

y y

τ _Qx τ _Qy τ _{М кр}

Рис.2.32.Напряженное состояние в точках внешнего контура коробчатого сечения

контура по всему периметру сечения, однако это требует большого объема вычислений и применения ЭВМ. Как минимум, вычисляют σ_ЭКВ в точках А, B, C, D, E ( см. рис.2.31) или же в аналогичных точках других квадрантов, в которых составляющие напряжения имеют одинаковые направления. После выявления максимальных эквивалентных напряжений их сравнивают с расчетным сопротивлением ( или с допускаемым напряжением) для проверки прочности.

Приведенные формулы достаточно точны для коробчатых сечений при условии, что отношения b / δ_П и h / δ_СТ находятся в пределах от 5…10 до 55…70. При более тонких стенках или поясах требуется проверка их местной устойчивости.

При предварительном определении геометрии сечения составных балок, исходя из требований прочности, находят момент сопротивления W_ТР, толщину стенки δ_СТ и площадь сечения поясов F_П с помощью зависимости

M

W_ТР ≥

[σ]_P

и приближенных выражений

Q

δ_СТ ≥ ;

h_СТ [τ]_{C P}

0,8 M_max

F_П ≥ ,

h¹ [σ]_P

где [σ]_P – допускаемое напряжение растяжения; [τ ]_{с р} – допускаемое напряжение среза; M_max – максимальный изгибающий момент; h¹ ≈ h_Б ≈ h_СТ – расстояние между центрами тяжести поясов; коэффициент 0,8 приближенно учитывает часть общего изгибающего момента, воспринимаемого поясами.

Проверка окончательно выбранных геометрических размеров элементов балок (поясов и стенки) производится по формулам

М

σ = ≤ [σ ]_P

W

и

Q S_БР

τ = ≤ [τ]_{C P},

J_БР δ_СТ

где S_БР – статический момент брутто полусечения относительно нейтральной оси; J_БР – момент инерции сечения брутто.

При изгибе в двух плоскостях

M_X y M_y x

σ = ± ≤ [σ]_P.

J_{X HT} J_{y HT}

Возможны и другие пути выбора высоты балки постоянного сечения, которая может быть определена как оптимальная с точки зрения минимума массы при обеспечении требуемого W_ТР. Полагая, что F – площадь сечения балки, F_{П –} площадь сечения пояса, имеем

F_П = 0,5 (F – h_СТ δ_СТ). (2.20)

Пренебрегая моментами инерции поясов ( из-за малости) относительно их собственных осей, при h_Б ≈ h_СТ, получим момент сопротивления двутавровой балки

h_СТ 2 2 δ_СТ h_СТ ³ 2 δ_СТh_СТ ²

W_ТР = 2 F_П + = F_Пh_СТ + .

2 h_СТ 12 h_СТ 6

(2.21)

Из (2.20) выразим

2W_ТР 2δ_СТh_СТ

F = + .

h_СТ 3

Приравнивая первую производную dF / dh_СТ нулю

dF 2W_ТР 2 δ_СТ

= – - + = 0,

dh_СТ h_СТ ² 3

найдем оптимальную высоту симметричного сечения балки постоянной жесткости

3 W_ТР

h_CТ^опт = . (2.22)

δ_СТ

Для коробчатой балки в (2.22) δ_СТ – толщина двух стенок.

Из (2.21) получим

W_ТР δ_СТ h_СТ

F_П = − .

h_СТ 6

С учетом (2.22) при выборе оптимальной высоты

δ_СТ h_СТ F_СТ

F_П = = ,

6 6

где F_СТ – площадь стенки двутавровой балки или площадь двух стенок коробчатой балки.

Пояс сварной балки представляет собой лист, максимальная толщина которого, исходя из требований хрупкой прочности, не должна превышать 50 мм для углеродистой стали и 40 мм – для низколегированной стали.

На рис.2.33 даны соотношения размеров ( b_Б, b¹, b¹¹) сжатых поясов балки из условия обеспечения их местной устойчивости при полном использовании материалов по прочности ( большие значения- для углеродистой стали,

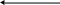b¹ ≤ (12…15) δ_П

δ_П

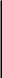
δ_СТ

b₁

h_СТ h¹

b¹¹ = (50…60)δ_П ≥ 300

b_Б

Рис.2.33.Геометрическая характеристика поперечного сечения

коробчатой балки

меньшие – для низколегированной). Минимальное расстояние между стенками коробчатой балки зависит от технологии и условий присоединения диафрагм. Балки, как правило, должны обладать также жесткостью в горизонтальной плоскости и на кручение. Для коробчатых мостовых кранов принимают L / b₁ ≤ 60 и h_СТ / b₁ ≤ 3,5 (см. рис. 2.33), где L – пролет балки.

Для снижения массы составных коробчатых балок целесообразно увеличивать размеры b и h при одновременном уменьшении толщины поясов δ_П и стенок δ_СТ. Однако при уменьшении отношений δ_СТ / h и δ_П / b возможна потеря местной устойчивости стенки или пояса. Согласно существующим рекомендациям при

h h E

< 90 и < 70 , (2.23)

δ_CТ δ_СТ [σ]

предел текучести в наиболее нагруженных точках сечения достигается раньше, чем произойдет потеря местной устойчивости. В этом случае укреплять основные элементы конструкции ребрами жесткости нецелесообразно.

При несоблюдении неравенств (2.23) необходимо применять ребра жесткости или диафрагмы. В современных коробчатых балках допускается h / δ_СТ ≤ (200…300) при δ_СТ ≥ (4…5) мм. При этом рекомендуется принимать расстояние между большими диафрагмами 1 (рис.2.34 ) ℓ = (1,5……2,0) h.. Диафрагмы могут быть сплошными или с отверстиями. Для обеспечения местной устойчивости стенок при действии нормальных напряжений в зоне сжатия устанавливают продольную диафрагму 3 на расстоянии (0,2…0,3) h от сжатого пояса. Между диафрагмой и полкой располагают малые диафрагмы 2, придающие конструкции дополнительную жесткость и выполняющие роль промежуточных опор для рельсов, по которым движется тележка, транспортирующая груз.

I I - I

1 ℓ

y

1

h x x

2 3

I y

L b

Рис.2.34. Схема размещения диафрагм: 1 – большой;

2 – промежуточной; 3 – продольной

Габаритные размеры сечения b и h ( см. рис.2.34) рекомендуется принимать с соблюдением неравенств:

L / b ≤ 60, h / b ≤ 3,5,

где L – длина балки.

Использование элементов жесткости при одновременном уменьшении толщин основных элементов является действенным средством снижения массы балки. Однако при этом конструкция усложняется и ее стоимость может увеличиться. Кроме того, конструкции нередко подвергаются действию местных сосредоточенных нагрузок, что накладывает ограничение на минимальную толщину основных элементов, которые не рекомендуется делать из листов толщиной менее 5 мм.

Каждому виду напряженного состояния соответствуют свои критические напряжения. Для опорных участков, где определяющими силовыми факторами являются поперечные силы, пластину рассматривают в состоянии равномерного сдвига; в этом случае для стенки с учетом ее упругого защемления в поясах

2 2

b δ

τ _КР = 1250 + 950 10 ³ , МПа,

a b

где а и b – большая и меньшая стороны пластины.

Коэффициент запаса местной устойчивости

τ _КР

n₀ = ≥ n,

τ

где n – коэффициент запаса прочности.

При этом касательные напряжения считаются усредненными:

Q

τ = .

h_СТ δ_СТ

Для средних участков, где определяющими факторами являются нормальные напряжения изгиба, критические напряжения для стенки коробчатой балки

2

δ_СТ

σ_КР = 7460 10 ³, МПа.

h_СТ