1.Etapa : Jednoduchá analýza rozptylu:

1.tabulka – p-hodnota, pokud je p>α → H0 nelze zamítnout = KONEC testu

2.Etapa: Podrobnější vyhodnocení výsledků anovy

1. Tabulka – p-hodnota, pokud je p<α → H0 se zamítá a pokračuje se mnohonásobným porovnáním, díky kterému zjišťujeme, které průměry se od sebe významně liší (označeny *) a které se od sebe liší jen náhodně. Používá se Scheffého metoda, alternativou může být Cramerova metoda.

Leveneho test – pro ověření shody rozptylů

Stejný postup ale počítá se s rozptyly

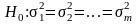
H₁ : alespoň jedna dvojice rozptylů se liší

Testy dobré shody χ²

H₀ : výběr pochází z daného rozdělení (např. normálního)

H_A : non H₀

NEPARAMETRICKÉ testy

- jsou nezávislé na tvaru rozdělení zkoumaných dat

-pro kvantitativní i kvalitativní data

-mají menší sílu – menší schopnost odhlásit nesprávnost testované hypotézy

-jednodušší na výpočet (výběry malého rozsahu)

• Dvouvýběrový Wilcoxonův test

• Wilcoxonův test

• Znaménkový test

• Kruskalův – Wallisův test

Dvouvýběrový Wilcoxonův test

- neparametrická analogie dvouvýběrového t-testu

- pro porovnání 2 nezávislých výběrů

Wilcoxonův test

- neparametrická analogie párového t-testu

- pro porovnání 2 závislých výběrů

1. Pro každou dvojici závislých porovnání vypočteme diferenci

2. Absolutním hodnotám diferencí přiřadíme pořadová čísla, nulové diference vynecháme

3. Sečteme zvlášť pořadová čísla kladných diferencí a záporných diferencí

4. Dostaneme tak součet W+ pro kladné diference a W- pro záporné diference

5. W = min (W+, W-) <= Wα

6. Wα najdeme podle zvolené hladiny významnosti α a podle počtu nenulových diferencí n

7. W = min <= Wα H0 zamítáme

Kruskalův – Wallisův test

- neparametrická obdoba jednoduché analýzy rozptylu

- test hypotézy, že m nezávislých výběrů s rozsahy n1, n2, …nm pochází z téhož rozdělení

11