Свойства первообразной[править | править вики-текст]

• Первообразная суммы равна сумме первообразных

• Первообразная произведения константы и функции равна произведению константы и первообразной функции

• У заданной на отрезке функции любые две первообразные отличаются на постоянную.

Формула, определяющая все первообразные функции f(x), называется неопределенным интегралом функции f(x) и обозначается символом

∫ f(x) dx.

При этом функция f(x) называется подынтегральной функцией, выражение f(x) dx — подынтегральным выражением, а символ ∫ — знаком интеграла. Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x) .

Свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной функции

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

d  ∫ f(x) dx = d(F(x) + C)= =(F(x)+ C)' dx = f(x) dx.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная функция:

∫  dF (x) = F(x) + C

или

∫ F '(x) dx = F(x) + C.

4.Свойство линейности неопределенного интегралаЕсли функции f(x) и g(x) имеют первообразные на некотором интервале, то функции f(x) ± g(x) и α·f(x) при любом α О R также имеют первообразные на этом интервале, причем

1. ∫ [f(x) ± g(x)] dx = ∫ f(x) dx ± ∫ g(x) dx

2. ∫ α · f(x) dx = α · ∫ f(x) dx     при α ≠ 0 

5. Если

∫ f(x) dx = F(x) + C

то для любых чисел a ≠ 0 и b

∫ f(a·x + b) dx   =   

1/а · F(a·x + b) + C

Утверждения о свойствах неопределенного интеграла проверяются дифференцированием.

46) Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который являетсятабличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл   Сделаем подстановку   где   — функция, имеющая непрерывную производную.

Тогда   и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

Или:

В частности, с помощью n-кратного применения этой формулы находится интеграл

где   — многочлен  -й степени.

47)

 По частям берутся интегралы следующих видов:

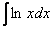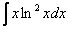1. ,  ,   – логарифм, логарифм, умноженный на какой-нибудь многочлен.

Пример 1

Найти неопределенный интеграл.

 В интегралах рассматриваемого типа за   всегда обозначается логарифм.

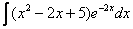2. ,  – экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде 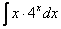  – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е»

Общее правило: за   всегда обозначается многочлен

Найти неопределенный интеграл.

Решение:

Используя знакомый алгоритм, интегрируем по частям:

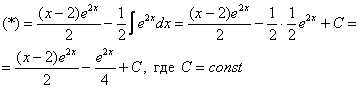
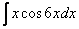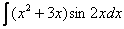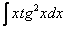3. ,  ,   – тригонометрические функции, умноженные на какой-нибудь многочлен.

Общее правило: за   всегда обозначается многочлен

Найти неопределенный интеграл.

Интегрируем по частям:

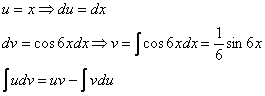
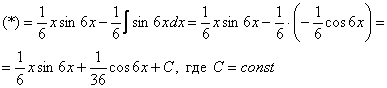
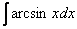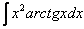4. ,   – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.

Общее правило: за   всегда обозначается обратная тригонометрическая функция.

Найти неопределенный интеграл.

Решаем.

Интегрируем по частям:

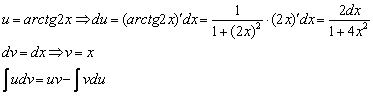
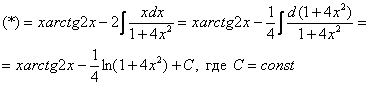
48)