35)Теорема Коши для дифференцируемых функций: Пусть

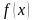1. и 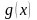непрерывны на ,

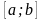2. и дифференцируемы хотя бы на ,

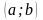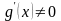3. на .

Тогда .

Убедимся, что 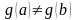. Если бы это было не так, то выполнялись бы все условия теоремы Ролля, и существовала бы точка 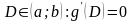, что противоречит третьему условию. Введём вспомогательную функцию .

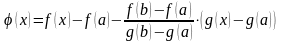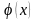непрерывна на как линейная комбинация непрерывных

дифференцируема на по той же причине, причём .

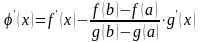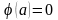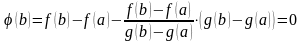, , т.е. .

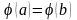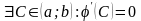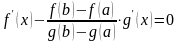Значит, по теореме Ролля , т.е. или .

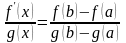36)Теорема Лопиталя:

Если:

1.  или  ;

2.  и   дифференцируемы в окрестности  ;

3.  в окрестности  ;

4. существует  ,

то существует  .

Пределы также могут быть односторонними.

Примеры:

37)Пусть функция   бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд

называется рядом Тейлора функции   в точке  .

То есть, рядом Тейлора для функции   в окрестности точки   называется степенной ряд относительно двучлена   вида

В форме Лагранжа:

Примеры:

38)Дифференцирование функции, заданной параметрически.

Предположим, что функция у= x(t) и y=φ(t) имеют производные, причём φ′ (t)не равна 0 на некотором промежутке. Из последнего неравенства вытекает строгая монотонность функции х= φ(t) по теореме о производной обратной функции t= φ(x) имеет производную φ′ (x)=1/ φ′(t), по теореме о производной сложной функции у= φ[φ(x)], имеем производную у′= φ′[φ(x)]* φ′(x), следовательно у′= φ′(t)/ φ′(t),

Где t= φ(x).

39) Условия возрастания(убывания) дифференцируемой ф-ции.

Теорема 1. Если во всех точках некоторого промежутка  , то функция  сохраняет в этом промежутке постоянное значение.Этот промежуток может быть замкнутым или открытым, конечным или бесконечным.

Теорема 2 (достаточный признак возрастания). Если вовсех точках некоторого промежутка  , то функция   возрастает в этом промежутке.

Теорема 3 (достаточный признак убывания). Если во всех точках некоторого промежутка  , то   убывает на этом промежутке.

Замечание. Условия теорем 2 и 3 не являются в полной мере необходимыми. Их можно несколько ослабить, а именно считать, что   или  , так как заключения теорем остаются справедливыми и тогда, когда производная обращается в нуль в конечном множестве точек.

40)Первое достаточное условие экстремума

Пусть функция f(x) дифференцируема в некоторой окрестности точки x0, кроме, быть может, самой точки x0, в которой, однако, функция непрерывна. Тогда:

Если производная f′(x) меняет знак с минуса на плюс при переходе через точку x0, (слева направо), то точка x0 является точкой строгого минимума (рис.2). Другими словами, в этом случае существует число δ>0, такое, что

∀x∈(x0−δ,x0)⇒f′(x)<0,

∀x∈(x0,x0+δ)⇒f′(x)>0.

Второе достаточное условие экстремума

Пусть в точке x0 первая производная равна нулю: f(x0)=0, т.е. точка x0 является стационарной точкойфункции f(x). Пусть также в этой точке существует вторая производная f′′(x0). Тогда:

Если f′′(x0)>0, то x0 является точкой строгого минимума функции f(x);

Если f′′(x0)<0, то x0 является точкой строгого максимума функции f(x).

третье достаточное условие экстремума

Пусть функция f(x) имеет в точке x0 производные до n-го порядка включительно. Тогда, если

f′(x0)=f′′(x0)=…=f(n−1)(x0)=0иf(n)(x0)≠0,

то при четном n точка x0 являетсяточкой строгого минимума, если f(n)(x0)>0, иточкой строгого максимума, если f(n)(x0)>0.

При нечетном n экстремума в точке x0 не существует.  Ясно, что при n=2 в качестве частного случая мы получаем рассмотренное выше второе достаточное условие экстремума. Чтобы исключить такой переход, в третьем признаке полагают, что n>2.